江苏省南通市通州区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-07-13 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分。在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）

1. 64的平方根是（）

A、8 B、 $\pm 8$ C、 $- 8$ D、 $\pm 4$

查看试题解析
2. 把点 $P_{1} (3 ， - 5)$ 向左平移2个单位长度，再向上平移3个单位长度到达点 $P_{2}$ 处，则点 $P_{2}$ 的坐标是（）

A、 $(5 ， - 2)$ B、 $(1 ， - 2)$ C、 $(5 ， - 7)$ D、 $(- 1 ， 2)$

查看试题解析
3. 下列事件中，最适合采用全面调查的是（）

A、对江苏省初中学生每天阅读时间的调查 B、对全国中学生节水意识的调查 C、对一枚用于发射卫星的运载火箭零部件的调查 D、对某批次灯泡使用寿命的调查

查看试题解析
4. 已知a，b是实数，若 $a > b$ ，则下列不等式正确的是（）

A、 $a - b < 0$ B、 $a + 2 < b + 2$ C、 $\frac{b}{a} > 1$ D、 $2 - 3 a < 2 - 3 b$

查看试题解析
5. 若 ${\begin{array}{l} x = 1 \\ y = - 2 \end{array}$ ，是关于x，y的二元一次方程 $a x + y = 3$ 的解，则a的值等于（）

A、0 B、1 C、3 D、5

查看试题解析
6. 若长度分别是a、3、5的三条线段能组成一个三角形，则a的值可以是（）

A、1 B、2 C、4 D、8

查看试题解析
7. 按下列给出的各条件，能画出大小、形状固定的 $△ A B C$ 的是（）

A、 $A B = 2 ， B C = 3 ， A C = 5$ B、 $A B = 2 ， B C = 3 ， ∠ B A C = 30 °$ C、 $A B = 2 ， B C = 3 ， ∠ A B C = 30 °$ D、 $∠ A = 70 ° ， ∠ B = 60 ° ， ∠ C = 50 °$

查看试题解析
8. 我国古代《四元玉鉴》中记载“二果问价”问题，其内容如下：九百九十九文钱，甜果苦果买一千，甜果九个十一文，苦果七个四文钱，试问甜苦果几个，又问各该几个钱？若设买甜果x个，买苦果y个，则符合题意的方程组是（）

A、 ${\begin{array}{l} x + y = 1000 \\ 99 x + 28 y = 999 \end{array}$ B、 ${\begin{array}{l} x + y = 1000 \\ \frac{9}{11} x + \frac{7}{4} y = 999 \end{array}$ C、 ${\begin{array}{l} x + y = 1000 \\ \frac{11}{9} x + \frac{4}{7} y = 999 \end{array}$ D、 ${\begin{array}{l} x + y = 999 \\ \frac{11}{9} x + \frac{4}{7} y = 1000 \end{array}$

查看试题解析
9. 已知关于x的不等式组 ${\begin{array}{l} x - a > 0 \\ 1 - x > 0 \end{array}$ 的解集中有且仅有3个整数，则a的取值范围是（）

A、 $- 3 < a \leq - 2$ B、 $- 3 < a < - 2$ C、 $- 3 \leq a < - 2$ D、 $- 3 \leq a \leq - 2$

查看试题解析
10. 如图，在五边形ABCDE中， $A B = A E = 4 ， B C = 3 ， D E = 2 ， ∠ A B C = ∠ A E D = 90 °$ ， $∠ D A C = \frac{1}{2} ∠ B A E$ ，则五边形ABCDE的面积等于（）

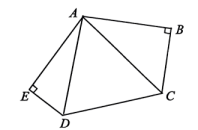A、16 B、20 C、24 D、26

查看试题解析

二、填空题（本大题共8小题，第11~12题每小题3分，第13~18题每小题4分，共30分。不需写出解答过程，请把答案直接填写在答题卡相应位置上）

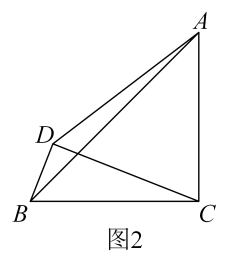
11. $\sqrt{5}$ 的相反数是．

查看试题解析
12. 若一个n边形的每个内角都为 $144 °$ ，则n的值等于．

查看试题解析
13. 已知点P在第二象限，且到x轴距离是1，到y轴距离是2，则点P的坐标为．

查看试题解析
14. 在一个盒子中装有若干乒乓球，小明为了探究盒子中所装乒乓球的数量，他先从盒子中取出一些乒乓球，记录了所取乒乓球的数量为 $m$ 个，并在这些乒乓球上做了记号“ $*$ ”，然后将它们放回盒子中，充分摇匀；接下来，他又从这个盒子中再次取出一些乒乓球，记录了所取乒乓球的数量为 $n$ 个，其中带有记号“ $*$ ”的乒乓球有 $p$ 个，小明根据实验所得的数据 $m = 20$ ， $n = 10$ ， $p = 2$ ，可估计出盒子中乒乓球的数量有个 $.$

查看试题解析
15. 如图， $∠ A C B = ∠ A C D$ ，要使 $△ A B C ≌ △ A D C$ ，只需添加一个条件，则这个条件可以是．

查看试题解析
16. 已知关于x，y的二元一次方程组 ${\begin{cases} 2 x + 3 y = 5 a \\ x + 4 y = 2 a + 3 \end{cases}$ 的解满足 $y < x$ ，则a的取值范围是．

查看试题解析
17. 如图，在 $△ A B C$ 中，点O是 $∠ A B C$ 和 $∠ A C B$ 的平分线的交点，点D是BC延长线上的点， $∠ O B C$ 和 $∠ O C D$ 的平分线交于点E， $∠ A = α$ ，则 $∠ E$ 的度数为．（用含 $α$ 的式子表示）

查看试题解析
18. 已知实数m，n，a，b满足 $m^{2} + a = b + 1 ， n^{2} + 2 b = 2 a + 4$ ，若 $k = m^{2} - 2 n^{2} + 3$ ，则k的取值范围是．

查看试题解析

三、解答题（本大题共8小题，共90分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）

19.

(1)、计算 $\sqrt{9} + \sqrt[3]{- 27} + | \sqrt{3} - 2 |$

(2)、解方程组 ${\begin{array}{l} 3 x + 4 y = 16 ， \\ 5 x - 6 y = 33 . \end{array}$

查看试题解析
20. 解不等式组 ${\begin{array}{l} 5 x + 2 \leq 4 x + 1 \\ \frac{x + 1}{4} > \frac{x - 3}{2} + 1 \end{array}$ ，并写出所有整数解．

查看试题解析
21. 已知点 $P (3 m + 6 ， m - 3)$ 请分别根据下列条件，求出点P的坐标．

(1)、点P在x轴上；

(2)、点P的纵坐标比横坐标大5；

(3)、点P在过点 $A (3 ， - 2)$ 且与y轴平行的直线上．

查看试题解析
22. 如图，在 $△ A B C$ 中， $∠ B = 80 ° ， ∠ C = 30 °$ ， AD平分 $∠ B A C$ ， AE是 $△ A B C$ 的高．

(1)、依题意补全图形；

(2)、求 $∠ D A E$ 的度数．

查看试题解析

23. 2023年3月22日是第三十一届“世界水日”，某校举行了水资源保护知识竞赛．为了了解本次知识竞赛成绩的分布情况，从参赛学生中随机抽取了部分同学的成绩整理描述（满分为100分，得分均为整数），绘制成两幅不完整的统计图表．

成绩x（分）	频数（人）	百分比
$60 \leq x < 70$	15	$10 %$
$70 \leq x < 80$	m	$20 %$
$80 \leq x < 90$	60	n
$90 \leq x < 100$	45

试根据以上信息解答下列问题：

(1)、在本次随机抽取的样本中，调查的学生人数是人；

(2)、补全频数分布直方图；

(3)、若该校七年级共有学生800人，估计有多少学生的测试成绩不低于90分？

查看试题解析

24. 2023年5月20日是第34个中国学生营养日，本次宣传主题为“科学食养，助力儿童健康成长”．某学校为学生提供的400克早餐食品中，蛋白质总含量为

7 ． 55 %

，包括一份粮谷类食品，一份牛奶和一个鸡蛋（一个鸡蛋的质量约为60克，蛋白质含量占

12 ． 5 %

；粮谷类食品和牛奶的部分营养成分如表所示）

粮谷类食品		牛奶
项目	每100克	项目	每100克
能量	2132千焦	能量	256千焦
脂肪	30.8克	脂肪	3.8克
蛋白质	8.0克	蛋白质	3.0克
碳水化合物	52.6克	碳水化合物	4.6克
钠	320毫克	钙	116毫克

(1)、设该份早餐中粮谷类食品为x克，牛奶为y克，请写出粮谷类食品中所含的蛋白质为克，牛奶中所含的蛋白质为克；（用含有x，y的式子表示）

(2)、请求出x，y的值；

(3)、该学校为学生提供的午餐有A，B两种套餐（每天只提供一种）：

套餐	主食（克）	肉类（克）	水果（克）	其它（克）
A	160	95	120	125
B	200	70	140	90

为了膳食平衡，建议合理控制学生的主食摄入量．如果在一周里，学生午餐主食摄入总量不超过890克，那么该校在一周里可以选择A，B套餐各几天？写出所有的方案．（说明：一周按5天计算）

查看试题解析

25.

(1)、如图1，在 $R t △ A B C$ 中， $A C = B C ， ∠ A C B = 90 ° ， B D ⊥ C D$ 于点D， $A E ⊥ C D$ 于点E．求证： $C D = A E$ ；

(2)、如图2，在 $R t △ A B C$ 中， $A C = B C ， ∠ A C B = ∠ C D B = 90 ° ， C D = 5$ ．求 $△ A C D$ 的面积；

(3)、已知， $A (- 2 ， - 5)$ ，点B和点C分别是y轴和x轴上一点，且满足 $A C = B C ， ∠ A C B = 90 °$ ．请直接写出点B和点C的坐标．

查看试题解析
26. 定义：在平面直角坐标系 $x O y$ 中，已知点 $M_{1} ， M_{2} ， M_{3}$ ，且 $M_{1} M_{2} ∥ y$ 轴， $M_{2} M_{3} ∥ x$ 轴，这三个点中任意两个点之间的距离的最小值称为点 $M_{1} ， M_{2} ， M_{3}$ 的“近距”．例如：点 $M_{1} (1 ， 2) ， M_{2} (1 ， - 1) ， M_{3} (- 3 ， - 1)$ 的“近距”是3．

(1)、已知， $A (3 ， 1) ， B (3 ， 7) ， C (x ， 7)$ ．
①若A，B，C的“近距”是4，则x的值为；

②点A，B，C的“近距”的最大值为；

(2)、已知点 $D (8 ， 0) ， E (0 ， - 4)$ ，点 $P (m ， n)$ 为线段DE上一动点．当 $F (1 ， 0)$ ， $G (1 ， n)$ ， $P (m ， n)$ 的“近距”最大时，求此时点P的坐标．

查看试题解析