江苏省南京市玄武区2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-07-13 类型:期末考试
一、选择题(本大题共6小题,每小题2分,共12分.在每小题所给出的四个选项中,恰有一项是符合题目要求的。)
-
1. 下列计算结果为的是( )A、 B、 C、 D、2. 关于的二元一次方程的一个解是 , 则的值为( )A、 B、 C、 D、3. 若 , 则下列不等式不成立的是( )A、 B、 C、 D、4. 如图,在中, , 过点的直线 , 若 , 则的度数是( )
 A、 B、 C、 D、5. 从地到地需要经过一段上坡路和一段平路,小明上坡速度为 , 平路速度为 , 下坡速度为 . 已知他从地到地需用 , 从地返回地需用24min.问从地到地全程是多少千米?我们可将这个实际问题转化为二元一次方程组问题,如果设未知数、 , 且列出一个方程为 , 则另一个方程是( )A、 B、 C、 D、6. 如图, , 点是外一点(点不在直线、、上),连接、 . 若 , , , 对于①;②;③;④ , 则的度数可能是( )
A、 B、 C、 D、5. 从地到地需要经过一段上坡路和一段平路,小明上坡速度为 , 平路速度为 , 下坡速度为 . 已知他从地到地需用 , 从地返回地需用24min.问从地到地全程是多少千米?我们可将这个实际问题转化为二元一次方程组问题,如果设未知数、 , 且列出一个方程为 , 则另一个方程是( )A、 B、 C、 D、6. 如图, , 点是外一点(点不在直线、、上),连接、 . 若 , , , 对于①;②;③;④ , 则的度数可能是( ) A、①④ B、②③④ C、①②③ D、①②③④
A、①④ B、②③④ C、①②③ D、①②③④二、填空题(本大题共10小题,每小题2分,共20分.)
-
7. 近来中国芯片技术获得重大突破,芯片已经量产,已知 , 将数据0.0000007用科学记数法表示为 .8. 分解因式的结果是9. 如图,直线与相交, , , 要使直线与平行,则直线绕点顺时针旋转的角度至少是°.
 10. 若 , , 则 .11. 若一个多边形的每一个外角都为 , 则这个多边形的内角和是 .12. 如图,将沿方向平移至的位置,若的面积是 , 平移的距离是的2倍,则四边形的面积为 .
10. 若 , , 则 .11. 若一个多边形的每一个外角都为 , 则这个多边形的内角和是 .12. 如图,将沿方向平移至的位置,若的面积是 , 平移的距离是的2倍,则四边形的面积为 . 13. 由方程组可得 . (用只含x的代数式表示)14. 已知关于的不等式的正整数解有且只有2个,则的取值范围为 .15. 如图,将一副三角板的直角顶点重合,则下列结论:①如果 , 则;②;③如果 , 则;④如果 , 则;其中所有正确的结论序号有 .
13. 由方程组可得 . (用只含x的代数式表示)14. 已知关于的不等式的正整数解有且只有2个,则的取值范围为 .15. 如图,将一副三角板的直角顶点重合,则下列结论:①如果 , 则;②;③如果 , 则;④如果 , 则;其中所有正确的结论序号有 . 16. 如图,在中,点分别在上, , , 、相交于点 . 若的面积为 , 则四边形的面积是 . (用含的代数式表示)
16. 如图,在中,点分别在上, , , 、相交于点 . 若的面积为 , 则四边形的面积是 . (用含的代数式表示)
三、解答题(本大题共68分.)
-
17. 计算:(1)、;(2)、 .18. 分解因式:(1)、;(2)、 .19. 解方程组20. 解不等式组并把解集在数轴上表示出.
 21. 请把下面的证明过程补充完整.
21. 请把下面的证明过程补充完整.已知:如图,是的高,点在上,在上, , .

求证: .
证明:∵是的高.
∴(三角形高线的定义).
∴( ).
∴(直角三角形两个锐角互余),
又∵(已知),
∴ ▲ ( ).
又∵(已知),
∴( ).
∴( ).
22. 3台大收割机和1台小收割机同时工作4小时共收割小麦7.2公顷,2台大收割机和3台小收割机同时工作3小时共收揢小麦5.7公顷.1台大收割机和1台小收割机每小时各收割小麦多少公顷?23. 如图,在数轴上,点分别表示数 , , 且点在点的左侧.(1)、求的取值范围;(2)、若点表示的数是关于的不等式的解,求的整数解. 24. 如图,在中, , 是线段延长线上的动点,在线段上取一点 , 使 .
24. 如图,在中, , 是线段延长线上的动点,在线段上取一点 , 使 .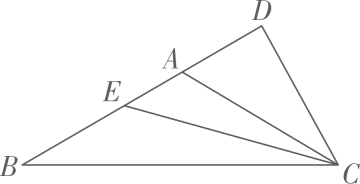 (1)、当点在线段上时,且 , 求的度数;(2)、若 , 且是直角三角形,则°25. 某水果店经销甲、乙两种水果,两次购进水果的情况如下表所示:
(1)、当点在线段上时,且 , 求的度数;(2)、若 , 且是直角三角形,则°25. 某水果店经销甲、乙两种水果,两次购进水果的情况如下表所示:进货批次 甲种水果(单位:千克)
乙种水果(单位:千克 总费用(单位:元) 第一次
80
50
2500
第二次
40
70
2420
(1)、求甲、乙两种水果的进价;(2)、第一次和第二次购进的水果全部售完后,第三次又购进甲、乙两种水果共150千克,购买的资金不超过3240元;①求购进的甲种水果至少为多少千克?
②第三次购进的甲、乙两种水果的售价分别为22元/千克、35元/千克.由于失水和腐烂,甲种水果减少了千克,乙种水果减少了千克.若第三次购进的水果全部售出后,获得的最大利润为1134元,则常数的值为 .
26. 定义:有一组对角互补的四边形叫做对补四边形.
 (1)、已知四边形是对补四边形.
(1)、已知四边形是对补四边形.①若 , 则 °.
②如图①,、的平分线分别与相交于点 , 且 .
求证:;(2)、如图②,在四边形中,对角线交于点 , 且平分 , , 平分 , 与交于点 , 且于点 , 则四边形是对补四边形吗?请说明理由;(3)、已知四边形是对补四边形,其三个顶点如图③所示,连接 . 若平分 , 平分 , 且直线 , 交于点(与点不重合),请直接写出与之间的数量关系