江苏省宿迁市宿城区2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-07-13 类型:期末考试
一、选择题(本大题共8小题,每小题3分,共24分.)
-
1. 下列运算中,正确的是( )A、 B、 C、 D、2. 如图,将三角尺的直角顶点放在直尺的一边上, , , 则的度数等于( )
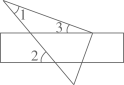 A、20° B、25° C、30° D、35°3. 已知 , 则下列不等式成立的是( )A、 B、 C、 D、4. 若三角形的两边a、b的长分别为3和4,则其第三边c的取值范围是( )A、 B、 C、 D、5. 下列命题是真命题的是( )A、两直线平行,同旁内角相等 B、相等的角是对顶角 C、三角形的外角大于任一内角 D、直角三角形的两锐角互余6. 如果是关于和的二元一次方程的解,那么的值是( )A、 B、 C、 D、7. 如图,直线 , 点A在直线a上,点C、D在直线b上,且 , 平分 , 若 , 则的度数是( )
A、20° B、25° C、30° D、35°3. 已知 , 则下列不等式成立的是( )A、 B、 C、 D、4. 若三角形的两边a、b的长分别为3和4,则其第三边c的取值范围是( )A、 B、 C、 D、5. 下列命题是真命题的是( )A、两直线平行,同旁内角相等 B、相等的角是对顶角 C、三角形的外角大于任一内角 D、直角三角形的两锐角互余6. 如果是关于和的二元一次方程的解,那么的值是( )A、 B、 C、 D、7. 如图,直线 , 点A在直线a上,点C、D在直线b上,且 , 平分 , 若 , 则的度数是( )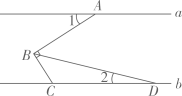 A、13° B、15° C、14° D、16°8. 若关于x的一元一次不等式组有4个整数解,则m的取值范围为( )A、 B、 C、 D、
A、13° B、15° C、14° D、16°8. 若关于x的一元一次不等式组有4个整数解,则m的取值范围为( )A、 B、 C、 D、二、填空题(本大题共10小题,每小题3分,共30分.)
-
9. 计算: .10. 已知2x+y=8,用含x的代数式表示y,则y= .11. 写出命题“如果 ,那么 互为倒数”的逆命题:.12. 如图,该数轴表示的不等式的解集为.
 13. 如图,把一张长方形纸片沿折叠, , 则度.
13. 如图,把一张长方形纸片沿折叠, , 则度.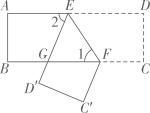 14. 如果 , 则.15. 某多边形内角和是外角和的2倍,则该多边形的边数.16. 若 , 且 , 求a的取值范围.17. 如图,的度数是.
14. 如果 , 则.15. 某多边形内角和是外角和的2倍,则该多边形的边数.16. 若 , 且 , 求a的取值范围.17. 如图,的度数是.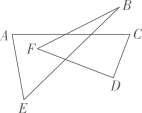 18. 如图,在中, , , M是射线上的一个动点,过点M作交射线于点N,连接 , 若中有两个角相等,则的度数可能是.
18. 如图,在中, , , M是射线上的一个动点,过点M作交射线于点N,连接 , 若中有两个角相等,则的度数可能是.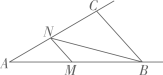
三、解答题(本大题共10题,共96分.解答时应写出必要的文字说明、证明过程或演算步骤)
-
19.(1)、计算:.(2)、分解因式:.20. 解方程组: .21. 解不等式组: , 并写出它的所有整数解.22. 先化简,再求值: , 其中.23. 如图,已知: , , 求证.
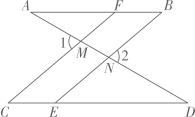
证明:∵(已知),
又∵ ▲ (对顶角相等),
(等量代换),
,
( )
又(已知),
▲ (等量代换),
( )