湖北省武汉市武昌区2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-07-13 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分,下列各题中均有四个备选答案,其中有且只有一个正确.)
-
1. 能使有意义的的取值范围是( )A、 B、 C、 D、2. 下列二次根式中,与是同类二次根式的是( )A、 B、 C、 D、3. 下表记录了甲、乙、丙、丁四位选手各20次射击成绩的数据信息.
选手
甲
乙
丙
丁
平均数(环)
9.3
9.6
9.6
9.3
方差(环)
0.034
0.012
0.034
0.012
请你根据表中数据选一人参加比赛,最合适的人选是( )
A、甲 B、乙 C、丙 D、丁4. 下列各式计算正确的是( )A、 B、 C、 D、5. 在中, , 则( )A、1 B、2 C、 D、6. 如果一次函数的图象不经过第二象限,那么的取值范围是( )A、 B、 C、 D、7. 如图,在四边形中, , 添加下列一个条件后,一定能判定四边形是平行四边形的是( ) A、 B、 C、 D、8. 一次函数和与的部分对应值如表1,与的部分对应值如表2:
A、 B、 C、 D、8. 一次函数和与的部分对应值如表1,与的部分对应值如表2:0
1
0
1
3
5
0
-1
则当时,的取值范围是( )
A、 B、 C、 D、9. 如图,矩形被直线分成面积相等的两部分, , 若线段的长是正整数,则矩形面积的最小值是( ) A、 B、81 C、 D、12110. 若直线和直线(为正整数)与轴围成的三角形面积记为 , 则的最小值为( )A、 B、 C、 D、
A、 B、81 C、 D、12110. 若直线和直线(为正整数)与轴围成的三角形面积记为 , 则的最小值为( )A、 B、 C、 D、二、填空题(本题共6小题,每小题3分,共18分)
-
11. 计算 的结果是.12. 在学校演讲比赛中,童威的得分为:演讲内容90分,演讲能力95分,演讲效果89分,若演讲内容、演讲能力、演讲效果按照的比确定,则童威的最终成绩是 .13. 直线向下平移1个单位后所得的直线与轴交点的坐标是 .14. 已知一个菱形的边长是 , 一个内角为 , 则这个菱形的面积是 .15. 小明同学在研究函数(为常数)时,得到以下四个结论:
①当时,随的增大而增大;②当时,有最小值0,没有最大值;
③该函数的图象关于轴对称;④若该函数的图象与直线(为常数)至少有3个交点,则 . 其中正确的结论是 . (请填写序号)
16. 如图,正方形内有一点 , 连接 , , 过点作交于 , 过点作交于 . 若 , 则的长是 . (请用含的式子表示)
三、解答题(共8个小题,共72分)
-
17. 计算:(1)、(2)、18. 如图,正方形中,点分别在的延长线上, , 连接 , .
 (1)、求证:;(2)、若四边形的面积是30, , 则的长为 .19. 学校组织学生参加知识竞赛活动,张老师随机抽取了部分同学的成绩(满分100分),按成绩划分为四个等级,并制作了如下不完整的统计表和统计图.
(1)、求证:;(2)、若四边形的面积是30, , 则的长为 .19. 学校组织学生参加知识竞赛活动,张老师随机抽取了部分同学的成绩(满分100分),按成绩划分为四个等级,并制作了如下不完整的统计表和统计图.等级
成绩分
人数
A
24
B
18
C
D

请根据图中提供的信息解答下列问题:
(1)、本次抽取的学生共有人,表中a的值为;(2)、所抽取学生成绩的中位数落在等级(填“A”,“B”,“C”或“D”)(3)、该校共组织了900名学生参加知识竞赛活动,请估计其中竞赛成绩达到80分以上(含80分)的学生人数.20. 如图,在平面直角坐标系中,一次函数的图象经过点 , 与轴和轴分别相交于点和点 , 与正比例函数的图象相交于点 , 点的纵坐标为3.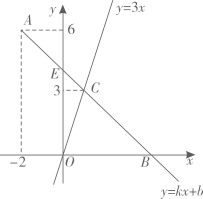 (1)、求一次函数的解析式;(2)、若点在轴上,满足 , 求点的坐标.(3)、若直线与的三边有两个公共点,则的取值范围是 .21. 如图是由小正方形组成的网格,每个小正方形顶点叫做格点.的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)、求一次函数的解析式;(2)、若点在轴上,满足 , 求点的坐标.(3)、若直线与的三边有两个公共点,则的取值范围是 .21. 如图是由小正方形组成的网格,每个小正方形顶点叫做格点.的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示. (1)、在图1中画平行四边形;点是边上一点,在边上找一点 , 使得;(2)、在图2中找一格点 , 画直线 , 使得;在直线上取一点 , 使得与关于对称.22. 已知甲、乙两个仓库分别有物资800吨和1200吨,现要把这些物资全部运往A,B两地,A地需要物资1300吨,B地需要物资700吨,从甲、乙两仓库把物资运往A,B两地的运费单价如下表:
(1)、在图1中画平行四边形;点是边上一点,在边上找一点 , 使得;(2)、在图2中找一格点 , 画直线 , 使得;在直线上取一点 , 使得与关于对称.22. 已知甲、乙两个仓库分别有物资800吨和1200吨,现要把这些物资全部运往A,B两地,A地需要物资1300吨,B地需要物资700吨,从甲、乙两仓库把物资运往A,B两地的运费单价如下表:A地(元/吨)
B地(元/吨)
甲仓库
12
15
乙仓库
10
18
(1)、设甲仓库运往地吨物资,直接写出总运费(元)关于(吨)的函数解析式(不需要写出自变量的取值范围);(2)、当甲仓库运往地多少吨物资时,总运费最省?最省的总运费是多少元?(3)、若甲仓库运往地的运费下降了元/吨后(且为常数),最省的总运费为23100元,求的值.23. 如图1,在正方形中,点分别在边上,于点 . (1)、如图2,若点与点重合,求证:;(2)、如图1,若点是的中点,连接交于点 , 求证: .(3)、如图3,将矩形沿折叠,点落在点处,点落在边上的点处,连接交于点 , 连接 , 若 , 直接写出的最小值为(用含的式子表示).24. 如图1,在平面直角坐标系中,点 , 直线与线段交于点 , 点在轴上, .
(1)、如图2,若点与点重合,求证:;(2)、如图1,若点是的中点,连接交于点 , 求证: .(3)、如图3,将矩形沿折叠,点落在点处,点落在边上的点处,连接交于点 , 连接 , 若 , 直接写出的最小值为(用含的式子表示).24. 如图1,在平面直角坐标系中,点 , 直线与线段交于点 , 点在轴上, .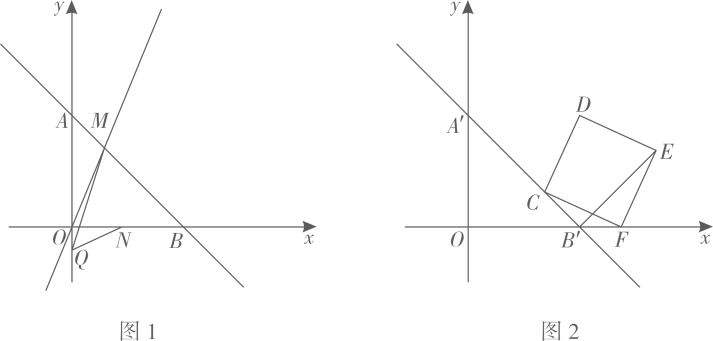 (1)、直接写出直线的解析式为;(2)、求点的坐标;(3)、如图2,将(1)中的直线向上平移个单位得到直线 , 点是射线上的一动点,点的坐标是 , 以为边向右作正方形 , 连接 , , 其中 , 直接写出点的坐标为(用的式子表示).
(1)、直接写出直线的解析式为;(2)、求点的坐标;(3)、如图2,将(1)中的直线向上平移个单位得到直线 , 点是射线上的一动点,点的坐标是 , 以为边向右作正方形 , 连接 , , 其中 , 直接写出点的坐标为(用的式子表示).