河南省鹤壁市2022-2023学年七年级下学期期末数学试题
试卷更新日期:2023-07-13 类型:期末考试
一、选择题(每小题3分,共30分,下列各小题均有四个答案其中只有1个是正确的.)
-
1. 如果方程是关于x的一元一次方程,则n的值为( )A、2 B、3 C、4 D、52. 下列方程的变形正确的是( )A、 , 去分母,得 B、 , 去括号,得 C、 , 移项,得 D、 , 系数化为1,得3. 若是关于y的二元一次方程,则的值为( )A、2023 B、 C、1 D、4. 某市举行中学生足球比赛,每队胜一场得3分,负一场得1分,本次足球比赛没有平局,下表是市实验学校比赛信息(不完整),则该校获胜的场数为( )
胜
负
合计
场数
y
12
积分
28
A、6场 B、7场 C、8场 D、9场5. 不等式组的解集在数轴(如图所示)上表示正确的是( )A、 B、
B、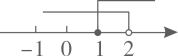 C、
C、 D、
D、 6. 2022年4月,教育部正式印发《义务教育课程方案(2022年版)》,将劳动从原来的综合实践活动课程中完全独立出来.某学校组织七年级学生到劳动实践教育基地参加实践活动,某小组的任务是平整土地 , 学校要求完成全部任务的时间不超过3小时.开始的半小时,由于操作不熟练,只平整了 . 若设他们在剩余时间内每小时平整土地 , 则根据题意可列不等式为( )A、 B、 C、 D、7. 以下说法:①如果三角形三个内角的比是 , 那么这个三角形是直角三角形;②如果三角形的一个外角等于与它相邻的内角,则这个三角形是直角三角形;③如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是直角三角形;④如果 , 那么是直角三角形;⑤在中,若 , 则此三角形是直角三角形.其中说法正确的个数有( )A、2个 B、3个 C、4个 D、5个8. 用三种不同的正多边形能够铺满地面的是( )A、正三角形、正方形、正五边形 B、正三角形、正方形、正六边形 C、正三角形、正方形、正七边形 D、正三角形、正方形、正八边形9. 在如图所示的图形中,不是轴对称图形的是( )A、
6. 2022年4月,教育部正式印发《义务教育课程方案(2022年版)》,将劳动从原来的综合实践活动课程中完全独立出来.某学校组织七年级学生到劳动实践教育基地参加实践活动,某小组的任务是平整土地 , 学校要求完成全部任务的时间不超过3小时.开始的半小时,由于操作不熟练,只平整了 . 若设他们在剩余时间内每小时平整土地 , 则根据题意可列不等式为( )A、 B、 C、 D、7. 以下说法:①如果三角形三个内角的比是 , 那么这个三角形是直角三角形;②如果三角形的一个外角等于与它相邻的内角,则这个三角形是直角三角形;③如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是直角三角形;④如果 , 那么是直角三角形;⑤在中,若 , 则此三角形是直角三角形.其中说法正确的个数有( )A、2个 B、3个 C、4个 D、5个8. 用三种不同的正多边形能够铺满地面的是( )A、正三角形、正方形、正五边形 B、正三角形、正方形、正六边形 C、正三角形、正方形、正七边形 D、正三角形、正方形、正八边形9. 在如图所示的图形中,不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图所示,将沿着某P方向平移一定的距离得到 , 则下列结论不成立的是( )
10. 如图所示,将沿着某P方向平移一定的距离得到 , 则下列结论不成立的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共15分)
-
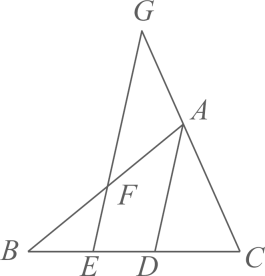
11. 写出一个以为解的一元一次方程:(任写一个即可).12. 若关于x、y的方程组的解互为相反数,则a的值是 .13. 若不等式的最小整数解是方程的解,则m的值为 .14. 如图所示,在中,是的平分线,交于点E,交于点F,交的延长线于点G.若 , , 则 .
 15. 已知的三边长分别为3,4,5,的三边长分别为3, , 若这两个三角形全等,则x的值为 .
15. 已知的三边长分别为3,4,5,的三边长分别为3, , 若这两个三角形全等,则x的值为 .三、解答题(本大题共8个小题,满分75分)
-
16.(1)、解方程:;(2)、解方程组:17. 在数学实践课上,小明在解方程时,因为粗心,去分母时方程左边的1没有乘10,从而求得方程的解为 , 试求的值及原方程正确的解.18. 解不等式组写出不等式组的所有整数解,并将解集在数轴上表示出来.19.(1)、分析图1①,②,④中阴影部分的分布规律,按此规律,在图1③中画出其中的阴影部分;
 (2)、在的正方形网格中,请你用两种不同方法,分别在图2①、②中再将两个空白的小正方形涂黑,使每个图形中的涂黑部分连同整个正方形网格成为轴对称图形.
(2)、在的正方形网格中,请你用两种不同方法,分别在图2①、②中再将两个空白的小正方形涂黑,使每个图形中的涂黑部分连同整个正方形网格成为轴对称图形.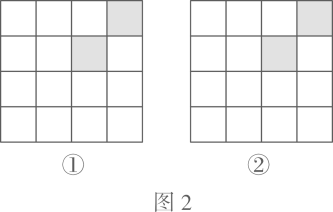 20. 已知一个多边形的内角和比它的外角和的3倍多 .(1)、求这个多边形的边数;(2)、如果从这个多边形的一个顶点引出对角线,最多可以引条对角线.21. 如图所示,已知 , , , 交于点M,交于点P.
20. 已知一个多边形的内角和比它的外角和的3倍多 .(1)、求这个多边形的边数;(2)、如果从这个多边形的一个顶点引出对角线,最多可以引条对角线.21. 如图所示,已知 , , , 交于点M,交于点P.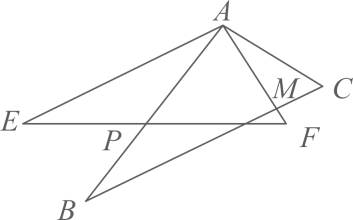 (1)、试说明:;(2)、可以经过某种变换得到 , 请你描述这个变换;(3)、求的度数.22. 第24庙冬奥会于2022年2月4日在北京举行,某经销商预测带有“冰墩墩”吉祥物标志的甲,乙两种纪念品可能会畅销,于是,该经销商用6200元一次性购进了甲、乙两种纪念品共100件.已知甲、乙两种纪念品的进价和售价如表:
(1)、试说明:;(2)、可以经过某种变换得到 , 请你描述这个变换;(3)、求的度数.22. 第24庙冬奥会于2022年2月4日在北京举行,某经销商预测带有“冰墩墩”吉祥物标志的甲,乙两种纪念品可能会畅销,于是,该经销商用6200元一次性购进了甲、乙两种纪念品共100件.已知甲、乙两种纪念品的进价和售价如表:种类
进价/(元/件)
售价/(元/件)
甲
50
100
乙
70
90
(1)、该经销商一次性购进甲、乙两种纪念品各多少件?(2)、如果在北京冬奥会开幕式当天销售完全部纪念品,则可获得利润为多少元?23. (1)、【感知】
(1)、【感知】如图1所示,在四边形中,分别是边的延长线,我们把称为四边形的外角,若 , 则;
(2)、【探究】如图2所示,在四边形中,分别是边的延长线,我们把称为四边形的外角,试探究与之间的数量关系,并说明理由;
(3)、【应用】如图3所示,分别是四边形的外角的平分线,若 , 则的度数为 .