江苏省南京市建邺区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-07-13 类型：期末考试

进入出卷网下载

一、选择题（本大题共6小题，每小题2分，共12分.在每小题所给出的四个选项中，恰有一项是符合题目要求的）

1. 下列计算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $2 a^{2} - a^{2} = 2$ C、 ${(a^{2})}^{3} = a^{5}$ D、 $2 a^{2} \div a^{2} = 2$

查看试题解析
2. 如图，下列条件中，可以判定 $D E ∥ A B$ 的是（）

A、 $∠ E = ∠ D C A$ B、 $∠ D C E = ∠ E$ C、 $∠ E + ∠ B C D = 180 °$ D、 $∠ A C E + ∠ E = 180 °$

查看试题解析
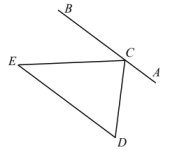3. 2023年4月26日，“第四代北斗芯片”正式发布，这是一款采用全新工艺的22纳米芯片.已知22纳米 $= 0.000000022$ 米，数据0.000000022用科学记数法可表示为（）

A、 $2.2 \times 1 0^{- 7}$ B、 $2.2 \times 1 0^{- 8}$ C、 $22 \times 1 0^{- 8}$ D、 $22 \times 1 0^{- 9}$

查看试题解析
4. 已知a、b、c分别表示一个三角形的三边长且 $a > b > c$ ，则下列不等式不成立的是（）

A、 $a + b > b + c$ B、 $a b > b c$ C、 $b + c > 2 a$ D、 $\frac{a}{b} < \frac{a}{c}$

查看试题解析
5. 如图，小明从点A出发沿直线前进5米到达点B，向左转x°后又沿直线前进5米到达点C，再向左转x°后沿直线前进5米到达点D……照这样走下去，小明第一次回到出发点A，一共走了60米，则x的值是（）

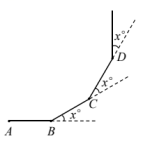A、90 B、45 C、30 D、15

查看试题解析
6. 下列说法中：①三角形三边高线的交点一定在三角形内部；②八边形有20条对角线；③两个连续偶数的平方差一定是8的倍数；④无论x取何值，代数式 $2 x^{2} - 2 x + 1$ 的值一定是正数.正确的有（）

A、②④ B、①② C、①③ D、③④

查看试题解析

二、填空题（本大题共10小题，每小题2分，共20分.）

7. 计算： $202 3^{0} =$ .

查看试题解析
8. x的 $\frac{1}{3}$ 与x的差为正数，用不等式表示为.

查看试题解析
9. 根据乘方的定义，补全计算过程： ${(a^{2})}^{3} =$ $= a^{2 + 2 + 2} = a^{6}$ .

查看试题解析
10. 命题“直角三角形的两个锐角互余”的逆命题是.

查看试题解析
11. 若 $(x + a) (x - 3) = x^{2} + 2 x - b$ ，则 $a - b$ .

查看试题解析
12. 若 $a < 1$ ，则 $- 2 a + 3$ 的取值范围为.

查看试题解析
13. 将一副直角三角板如图放置，已知 $∠ C = 60 °$ ， $∠ F = 45 °$ ，当 $D F ⊥ B C$ 时， $∠ E G B =$ .

查看试题解析
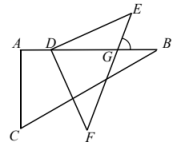14. 如图，将 $△ A B C$ 纸片先沿DE折叠，再沿FG折叠，若 $∠ 1 + ∠ 2 = 228 °$ ，则 $∠ 3 + ∠ 4 =$ .

查看试题解析
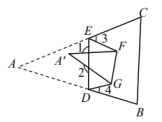15. 已知x、y满足 ${\begin{cases} 17 x + 19 y = 6 - a \\ 13 x - 7 y = 10 a + 1 \end{cases}$ ，则代数式 $x + y$ 的值为.

查看试题解析
16. 如图，在 $△ A B C$ 中，D是边AB的中点，E、F分别是边AC上的三等分点，连接BE、BF分别交CD于G、H点，若 $△ A B C$ 的面积为90，则四边形EFHG的面积为.

查看试题解析

三、解答题（本大题共68分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）

17. 计算：

(1)、 ${(- \frac{1}{2})}^{2} \div {(- 2)}^{3} \times {(- 2)}^{- 2}$ ；

(2)、 $a^{2} \cdot a^{4} + {(- a^{2})}^{3} - 2 {(- a^{3})}^{2}$ .

查看试题解析
18. 分解因式：

(1)、 $18 a^{2} - 32$ ；

(2)、 $y - 6 x y + 9 x^{2} y$ .

查看试题解析
19. 先化简，再求值： ${(2 a + b)}^{2} - (3 b + 2 a) (2 a - 3 b)$ ，其中， $a = 2$ ， $b = \frac{2}{5}$ .

查看试题解析
20. 解方程组 ${\begin{cases} x + 2 y = 0 \\ 3 x - 4 y = 5 \end{cases}$ .

查看试题解析
21. 解不等式组 ${\begin{cases} \frac{3 x - 2}{3} \geq 1 \\ 3 x + 5 > 4 x - 2 \end{cases}$ ，并写出该不等式组的整数解.

查看试题解析
22. 已知：如图，AD是 $△ A B C$ 的高，E是AC上一点， $E F ⊥ B C$ ，垂足为F，连接DE， $∠ 1 = ∠ 2$ .

(1)、求证： $D E ∥ A B$ .

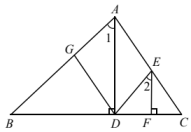(2)、过D作 $D G ∥ A C$ 交AB于G，当 $∠ B + ∠ C = 100 °$ 时， $∠ E D G =$ .

查看试题解析
23. 已知关于x的方程 $2 (x + a) = x + 3$ 的解适合不等式 $2 x - 10 > 8 a$ ，求a的取值范围.

查看试题解析
24. 是否存在正整数x和y，使得 $x^{2} = y^{2} + 2023$ ，若存在，求出满足条件的x和y的值；若不存在，请说明理由.

查看试题解析
25. 2023年9月23日至10月8日第十九届亚运会将在杭州举办.某商场用25000元购进亚运吉祥物的摆件和挂件，售完后共获利11700元.其中摆件每件进价40元，售价58元；挂件每件进价30元，售价45元.

(1)、请分别求出该商场购进摆件和挂件的数量.（用二元一次方程组解决问题）

(2)、618促销期间，商场第二次以原进价购进摆件和挂件，购进摆件的件数不变，而购进挂件的件数是第一次的2倍，摆件按原售价出售，而挂件打折销售.若摆件和挂件销售完毕，要使第二次经营活动获利不少于10800元，则挂件最低可以打几折？（用一元一次不等式解决问题）

查看试题解析
26. 在 $△ A B C$ 和 $△ A C D$ （共AC边且不重合）中， $∠ B = ∠ B A C$ ， $∠ D = ∠ D A C$ .

(1)、如图1，当 $△ A B C$ 和 $△ A C D$ 均为钝角三角形，B、D在直线AC两侧时， $∠ B C D$ 和 $∠ B A D$ 之间的数量关系为.

(2)、如图2，当 $△ A B C$ 和 $△ A C D$ 均为锐角三角形，且B、D在直线AC两侧时， $∠ B C D$ 和 $∠ B A D$ 之间的数量关系为.

(3)、如图3，当 $△ A B C$ 为钝角三角形， $△ A C D$ 为锐角三角形，且B、D在直线AC同侧时，求证： $∠ B C D = 2 ∠ B A D$ .

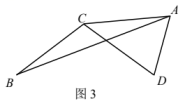(4)、分别作 $∠ B$ 和 $∠ D$ 的角平分线，两条角平分线所在直线交于P点（点P不与点B或者点D重合），当 $∠ B C D = 100 °$ 时，直接写出 $∠ B P D$ 的度数.

查看试题解析