湖北省武汉市武昌区2022-2023学年七年级下学期期末数学试题

试卷更新日期：2023-07-13 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. 在平面直角坐标系中，点 $P (a - 3 ， 2)$ 在第二象限，则a的取值范围是（）

A、a＜3 B、a≤3 C、a＜0 D、a＞3

查看试题解析
2. 16的平方根为（）

A、4 B、－4 C、±8 D、±4

查看试题解析
3. 下列实数中，是无理数的是（）

A、 $\sqrt{4}$ B、 $\sqrt{2}$ C、－3 D、3.14

查看试题解析
4. 关于x的某个不等式的解集在数轴上表示如图所示，则该不等式的解集是（）

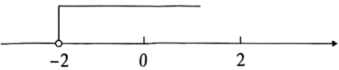A、x＞－2 B、x＜－2 C、x＞2 D、x≠－2

查看试题解析
5. 下列调查方式，你认为最合适的是（）

A、调查央视栏目《中国诗词大会》的收视率，采用全面调查 B、高铁站对上车旅客进行安检，采用抽样调查 C、了解全国七年级学生的睡眠情况，采用全面调查 D、了解湖北省居民的日平均用电量，采用抽样调查

查看试题解析
6. 若 ${\begin{cases} x = 2 \\ y = - 1 \end{cases}$ 是二元一次方程ax＋by＝2的一个解，则2a－b－4的值是（）

A、－6 B、－2 C、2 D、6

查看试题解析
7. 已知a＜b，则下列不等式中，不正确的是（）

A、a－2＜b－2 B、2a＜2b C、－2a＜－2b D、 $\frac{a}{2} < \frac{b}{2}$

查看试题解析
8. 下列命题正确的是（）

A、同位角相等 B、过一点有且只有一条直线与已知真线垂直 C、互补的两个角是邻补角 D、直线a，b，c，若a∥b，b∥c，则a∥c

查看试题解析
9. 如图，AB∥CD，EF⊥AB于点E，∠AEH＝∠FGH＝20°，∠H＝50°，则∠EFG的度数是（）

A、120° B、130° C、140° D、150°

查看试题解析
10. 将1，2，3，4，5，6，7，8，9，10这个10个自然数填到图中的10个格子里，每个格子中只填一个数，使得田字形的4个格子中所填数字之和都等于m．则m的最大值是（）

A、23 B、24 C、25 D、26

查看试题解析

二、填空题（本题共6小题，每小题3分，共18分）

11. 计算： $\sqrt[3]{64} =$ ．

查看试题解析
12. 已知一个样本数据：25，21，23，29，27，29，25，28，30，22，24，28，24，26，以2为组距可以分为组．

查看试题解析
13. 如图，直线AB与CD相交于点O，OE⊥CD，OF平分∠AOE，∠COF＝34°，则∠BOD的度数为．

查看试题解析
14. 已知 $\frac{a}{3} = \frac{b}{4} = \frac{c}{5}$ ，满足 $a - b + 2 c = 18$ ，则 $a + b + c =$ ．

查看试题解析
15. 若不等式 $\frac{2 x + 5}{3} - 1 ≤ 2 - x$ 解集中x的每一个值，都能使关于x的不等式 $3 (x - 1) + 5 > 5 x + 2 (m + x)$ 成立，则m的取值范围是．

查看试题解析
16. 如图，正方形ABCD的两个顶点 $A (0 ， 0)$ ， $C (6 ， 6)$ ，对正方形ABCD进行如下变换：把每个点的横、纵坐标都乘以同一个数a，将得到的点先向右平移m个单位，再向上平移n个单位（m＞0，n＞0），得到正方形 $A_{1} B_{1} C_{1} D_{1}$ ，其中B的对应点为 $B_{1} (\frac{5}{2} ， \frac{1}{3})$ ， D的对应点为 $D_{1} (\frac{1}{2} ， \frac{7}{3})$ ，若正方形ABCD内部的一个点F经过上述相同变换后得到的对应点 $F_{1}$ 与点F重合，则F点的坐标为．

查看试题解析

三、解答题（共8个小题，共72分）

17. 按要求解下列方程组：

(1)、（代入法） ${\begin{array}{l} y = x + 1 ① \\ 2 x + y = 4 ② \end{array}$

(2)、（加减法） ${\begin{array}{l} x - 2 y = 5 ① \\ 2 x + y = 5 ② \end{array}$

查看试题解析
18. 解不等式组 ${\begin{array}{l} x + 2 ≥ 1 ① \\ 4 x - 1 ≤ 2 x + 3 ② \end{array}$ ，请按下列步骤完成解答

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、将不等式①和②的解集在数轴上表示出来；

(4)、原不等式组的解集是．

查看试题解析
19. 如图，∠1＋∠2＝180°，∠3＝∠B，求证∠AED＝∠C．完成下面的证明过程．

证明：∵∠1＋∠2＝180°，∠1＋∠4＝180°，

∴∠2＝∠4（同角的补角相等）．

∴AB∥ ▲ （内错角相等，两直线平行）．

∴∠3＝∠ADE（）．

又∵∠3＝∠B（已知），

∴ ▲ ＝∠B（等量代换）﹒

∴DE∥BC（）．

∴∠AED＝∠C（两直线平行，同位角相等）．

查看试题解析
20. 中国共产党第二十次全国代表大会于2022年10月16日在北京召开，同称“二十大”．在会议召开期间，国家领导人就许多民众关心的热点问题进行了时论，并形成了许多的决议．为了了解民众对“二十大”相关政策的了解情况，对某小区居民进行了随机抽样调查，选取其中五个热点议题的关键词，分别为：“A．依法治国；B．社会保障；C．乡村振兴；D．教育改革；E．数字化生活”，每人只能从中选一个最关注的议题，根据调查结果绘制了两幅不完整的统计图，请结合统计图中的信息，解答下列问题：

(1)、扇形统计图中a＝；E所在扇形的圆心角度数为；

(2)、请把条形统计图补充完整；

(3)、若这个小区居民共有6500人，根据抽样调查的结果，估计该小区居民中最关注的议题是“教育改革”的大约有多少人？

查看试题解析
21. 如图，在平面直角坐标系中，有两点 $A (- 2 ， 3)$ ， $B (1 ， 5)$ ， AB交y轴于点C．

(1)、平移线段AB，使点A与原点O重合，点B平移后对应点为点D，在图1中画出线段OD；直接写出点D的坐标为；

(2)、连接OA，OB，求△OAB的面积；

(3)、直接写出点C的坐标为．

查看试题解析
22. 如图，A，B两地有公路和铁路相连，在这条路上有一家食品厂，它到B地的距离是到A地的2倍，这家厂从A地购买原料，制成食品卖到B地．已知公路运价为1.5元/（公里·吨），铁路运价为1元/（公里·吨），这两次运输（第一次：A地→食品厂第二次：食品厂→B地）共支付公路运费15600元，铁路运费20600元．

(1)、这家食品厂到A地的距离是多少公里？

(2)、此次购进了多少吨原料？制成了多少吨食品

(3)、这家食品厂准备再新进一批原料，加工成食品后全部卖出，已知买进的原料每吨5000元，卖出的食品每吨10000元，保持原料产出食品的效率不变，如果希望获得利润不少于1122940元，则至少要购进多少吨原料？（注：利润＝销售款－原料费－运输费）

查看试题解析
23.

(1)、【问题情境】
如图1，AB∥CD，直线EG交AB于点H，交CD于点G，点F在直线AB上．直接写出∠E，∠EFH，∠EGD之间的数量关系为．

(2)、【实践运用】
如图2，AB∥CD，直线EG交AB于点H，交CD于点G，点F在直线AB上．FT平分∠EFH，GM平分∠EGC，若∠E＝40°，求∠FMG的度数．

(3)、【拓广探索】
如图3，AB∥CD，直线EG交AB于点H，交CD于点G，点P为平面内不在直线AB，CD，EG上的一点，若∠BHP＝x，∠DGP＝y，则∠HPG＝（直接写出答案，用x，y表示）．

查看试题解析
24. 定义：使方程（组〉与不等式（组）同时成立的未知数的值称为此方程（组）和不等式（组）的“完美解”．
例：已知方程2x－3＝1与不等式x＋3＞0，当x＝2时，2x－3＝2×2－3＝1，x＋3＝2＋3＝5＞0同时成立，则称“x＝2”是方程2x－3＝1与不等式x＋3＞0的“完美解”．

(1)、已知①2x＋1＞3，②3x＋7＜4，③2－x＞2x＋1，则方程2x＋3＝1的解是不等式（填序号）的“完美解”；

(2)、若 ${\begin{array}{l} x = x_{0} \\ y = y_{0} \end{array}$ 是方程 $x - 3 y = 5$ 与不等式组 ${\begin{array}{l} x > 2 \\ y < 1 \end{array}$ 的“完美解”，求 $x_{0} + 3 y_{0}$ 的取值范围；

(3)、若 ${\begin{array}{l} x = x_{0} \\ y = y_{0} \end{array}$ （ $x_{0}$ ， $y_{0}$ 是整数）是方程组 ${\begin{array}{l} x + y = a \\ 4 x - 5 y = a + 3 \end{array}$ 与不等式组 ${\begin{array}{l} 2 x - 7 y < 1 \\ 5 x - 6 y < 14 \end{array}$ 的一组“完美解”，求整数a的值．

查看试题解析