（人教版）2023-2024学年八年级数学上册11.3多边形及其内角和 同步分层训练（培优卷）

试卷更新日期：2023-07-13 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 一个多边形最少可分割成五个三角形，则它是（    ）边形
    A、8 B、7 C、6 D、5

    查看试题解析

  • 2. 从一个多边形的一个顶点出发共可作10条对角线，则这个多边形共有对角线的条数为（   ）
    A、35 B、65 C、70 D、130

    查看试题解析

  • 3. 如图所示，要使一个六边形木架在同一平面内不变形，至少还要再钉上（    ）根木条.

    A、1 B、2 C、3 D、4

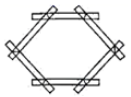    查看试题解析

  • 4. 三角形具有稳定性，所以要使如图所示的五边形木架不变形，至少要使钉上（   ）根木条

    A、1 B、2 C、3 D、4

    查看试题解析

  • 5. 从n边形的一个顶点作对角线，把这个n边形分成三角形的个数是(   )
    A、n B、n-1 C、n-2 D、n-3

    查看试题解析

  • 6. 将一长方形纸片沿一条直线剪成两个多边形，那么这两个多边形的内角和之和不可能是（    ）
    A、360° B、540° C、720° D、730°

    查看试题解析

  • 7. 如图，∠A+∠B+∠C+∠D+∠E+∠F的度数为（   ）

    A、180° B、360 C、270° D、540°

    查看试题解析

  • 8. 一个四边形，截一刀后得到的新多边形的内角和将（    ）
    A、增加180° B、减少180° C、不变 D、以上三种情况都有可能

    查看试题解析

  • 9.

    下图是由10把相同的折扇组成的“蝶恋花”（图1）和梅花图案（图2）（图中的折扇无重叠），则梅花图案中的五角星的五个锐角均为（　　）

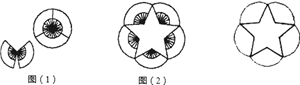    A、36° B、42° C、45° D、48°

    查看试题解析

  • 10. 如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，则∠A与∠1+∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，这个规律是（   ）

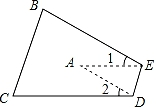    A、∠A＝∠1+∠2 B、2∠A＝∠1+∠2   C、3∠A＝2∠1+∠2 D、3∠A＝2（∠1+∠2）

    查看试题解析

二、填空题

  • 11. 过四边形的一个顶点可以画一条对角线，且把四边形分成两个三角形；过五边形的一个顶点可以画两条对角线，且把五边形分成三个三角形；......猜想：过n边形的一个顶点可以画条对角线，且把n边形分成 个三角形.

    查看试题解析

  • 12. 凸n边形的对角线的条数记作an(n≥4)，例如：a4=2，那么：①a5=；②a6-a5=；③an+1-an=(n≥4，用含n的代数式表示).

    查看试题解析

  • 13. 如图所示，△ABO与△CDO称为“对顶三角形”，其中∠A+∠B=∠C+∠D．利用这个结论，在图2中，∠A+∠B+∠C+∠D+∠E+∠F+∠G= °

    查看试题解析

  • 14. 在△ABC中，AD，BE为三角形的高，M为AD，BE所在直线的交点，∠BMD=50°，则∠C的度数是.

    查看试题解析

  • 15. 已知，在四边形ABCD中，∠F为四边形ABCD的∠ABC的平分线及外角∠DCE的平分线所在的直线构成的锐角，若∠A＝α，∠D＝β，

    (1)、如图①，当α+β＞180°时，∠F＝（用含α，β的式子表示）；
    (2)、如图②，当α+β＜180°时，请在图②中，画出∠F ， 且∠F＝（用含α，β的式子表示）；
    (3)、当α，β满足条件时，不存在∠F ．

    查看试题解析

三、解答题

  • 16. 探究归纳题：

    (1)、试验分析：

    如图1，经过A点可以作条对角线；同样，经过B点可以作条；经过C点可以作条；经过D点可以作条对角线.

    通过以上分析和总结，图1共有条对角线.

    (2)、拓展延伸：

    运用（1）的分析方法，可得：

    图2共有条对角线；

    图3共有条对角线；

    (3)、探索归纳：

    对于n边形(n>3)，共有条对角线．(用含n的式子表示)

    (4)、特例验证：

    十边形有条对角线.

    查看试题解析

  • 17. 已知：从 n 边形的一个顶点出发共有4条对角线；从 m 边形的一个顶点出发的所有对角线把 m 边形分成6个三角形；正 t 边形的边长为 7 ，周长为63．求 (n-m)t 的值．

    查看试题解析

  • 18. 如图，求 ∠A+∠B+∠C+∠D+∠E+∠F的大小．

    查看试题解析

  • 19. 求证：三角形的外角和等于360° ． 一般地，n边形的外角和等于360°

    查看试题解析

四、综合题

  • 20. 如图，⊙O是四边形ABCD的外接圆，AC是⊙O的直径，BE⊥DC ， 交DC的延长线于点E ， CB平分∠ACE ．

    (1)、求证：BE是⊙O的切线；
    (2)、若cos∠BAD=25 ， AC=10 ， 求CE的长．

    查看试题解析

  • 21. 如图①，∠1、∠2是四边形ABCD的两个不相邻的外角．

    (1)、猜想并说明∠1+∠2与∠A、∠C的数量关系；
    (2)、如图②，在四边形ABCD中，∠ABC与∠ADC的平分线交于点O．若∠A＝58°，∠C＝152°，求∠BOD的度数；
    (3)、如图③，BO、DO分别是四边形ABCD外角∠CBE、∠CDF的角平分线．请直接写出∠A、∠C与∠O的数量关系．

    查看试题解析

  • 22. 乐乐和数学小组的同学们研究多边形对角线的相关问题，邀请你也加入其中！请仔细观察下面的图形和表格，并回答下列问题：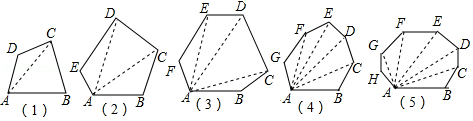

    多边形的顶点数

    4

    5

     6

     7

     8

     ……

    n

    从一个顶点出发的对角线的条数

    1

    2

    3

    4

    5

    ……

    ① 

         

     多边形对角线的总条数

    2

    5

    9

    14

    20

    ……

    ②

           
    (1)、观察探究 请自己观察上面的图形和表格，并用含n的代数式将上面的表格填写完整，其中①；②；
    (2)、实际应用 数学社团共分为6个小组，每组有3名同学．同学们约定，大年初一时不同组的两位同学之间要打一个电话拜年，请问，按照此约定，数学社团的同学们一共将拨打电话多少个？
    (3)、类比归纳 乐乐认为（1）、（2）之间存在某种联系，你能找到这两个问题之间的联系吗？请用语言描述你的发现．

    查看试题解析

  • 23. Pn表示n边形的对角线的交点个数（指落在其内部的交点），如果这些交点都不重合，那么Pn与n的关系式是：Pn= n(n−1)24 •（n2﹣an+b）（其中a，b是常数，n≥4）
    (1)、通过画图，可得：四边形时，P4=；五边形时，P5=
    (2)、请根据四边形和五边形对角线交点的个数，结合关系式，求a，b的值．

    查看试题解析