（人教版）2023-2024学年八年级数学上册11.3多边形及其内角和 同步分层训练（提升卷）
试卷更新日期：2023-07-13 类型：同步测试
一、选择题
-
1. 如图，要使一个七边形木架不变形，至少要再钉上木条的根数是（ ）
A、1根 B、2根 C、3根 D、4根2. 一个多边形从一个顶点引出的对角线条数是4，这个多边形的边数是（ ）A、4 B、5 C、6 D、73. 若n边形恰好有2n条对角线，则n为（ ）A、4 B、5 C、6 D、74. 一个多边形的内角和是外角和的2倍，则这个多边形对角线的条数是（ ）A、3 B、4 C、9 D、185. 一个正多边形的每一个内角是 ，则从这个正多边形的一个顶点出发可作（ ）条对角线．A、5 B、4 C、3 D、26. 以下关于多边形内角和与外角和的表述，错误的是（ ）A、四边形的内角和与外角和相等 B、如果一个四边形的一组对角互补，那么另一组对角也互补 C、六边形的内角和是外角和是2倍 D、如果一个多边形的每个内角是120°，那么它是十边形．7. 图1所示的是一把木工台锯时使用的六角尺，它能提供常用的几种测量角度．在图2的六角尺示意图中，x的值为（ ）
A、 B、 C、 D、8. 小红：我计算出一个多边形的内角和为；老师：不对呀，你可能少加了一个角则小红少加的这个角的度数是（ ）A、110° B、120° C、130° D、140°9. 已知一个多边形的内角和为 ， 则这个多边形是（ ）A、八边形 B、七边形 C、六边形 D、五边形10. 如图，在五边形公园中， ， 若张老师沿公园边由点经散步，则张老师共转了（ ）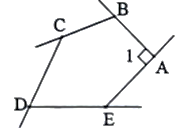
A、 B、 C、 D、二、填空题
-
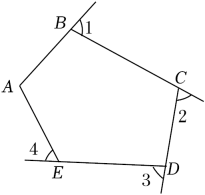
11. 一个凸 边形的边数与对角线条数的和小于20，且能被5整除，则 ．12. 若从一个多边形一个顶点出发，最多可以引12条对角线，则它的边数为 ．13. 画出一个正五边形的所有对角线，共有条．14. 若一个正多边形的内角是其外角的5倍，则这个正多边形的边数是.15. 如图，五边形ABCDE的一个内角∠A＝110°，则∠1+∠2+∠3+∠4等于 ．
三、解答题
-
16. 已知从m边形的一个顶点出发可以画4条对角线；从n边形的一个顶点出发的所有对角线把n边形分成6个三角形．求的值．17. 已知从n边形的一个顶点出发共有4条对角线，该n边形的周长为56，且各边长是连续的自然数，求这个多边形的各边长．18. 已知一个多边形的内角和为 ， 请求出这个多边形的边数并直接写出这个多边形对角线的总条数．19. 一个多边形的内角和比其外角和的3倍多180°，求这个多边形的边数．
四、综合题
-
20. 已知一个正多边形共有35条对角线，求：(1)、这个正多边形的边数(2)、这个正多边形每个内角和每个外角的度数21.
求解：根据问题回答：
(1)、如图（1），O为四边形ABCD内一点，连接OA、OB、OC、OC可以得几个三角形？它与边数有何关系？(2)、如图（2），O在五边形ABCDE的AB上，连接OC、OD、OE，可以得到几个三角形？它与边数有何关系？(3)、如图（3），过A作六边形ABCDEF的对角线，可以得到几个三角形？它与边数有何关系？22. 如图，在四边形中， ， 分别是及的平分线.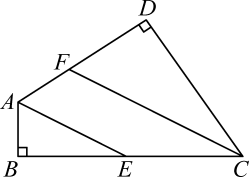
(1)、求证：；(2)、若 ， 求.23. 在△ABC中，∠A＝70°，点D、E分别是边AC、AB上的点（不与A、B、C重合）点P是平面内一动点（P与D、B不在同一直线上），设∠PEB＝∠1，∠DPE＝∠2，∠PDC＝∠3．
(1)、若点P在边BC上运动（不与点B和点C重合），如图（1）所示，则∠2＝；（用含有∠1、∠3的代数式表示）(2)、若点P在△ABC的外部，如图（2）所示，则∠1、∠2、∠3之间有何关系？写出你的结论，并说明理由．(3)、当点P在边CB的延长线上运动时，试画出相应图形，标注有关字母与数字，直接写出对应的∠1、∠2、∠3之间的关系式．