山东省淄博市淄川区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-12 类型:期末考试
一、单选题
-
1. 如图,一张圆桌共有3个座位,甲、乙,丙3人随机坐到这3个座位上,则甲和乙相邻的概率为( )
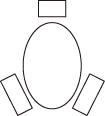 A、 B、 C、 D、2. 在 中, ,若 ,则 的形状为( )A、钝角三角形 B、等边三角形 C、直角三角形 D、不等边三角形3. 下列命题中,其逆命题是真命题的是( )A、对顶角相等 B、两直线平行,同位角相等 C、全等三角形的对应角相等 D、正方形的四个角都是直角4. 若 , 则下列不等式中正确的是( )A、 B、 C、 D、5. 如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A、 B、 C、 D、2. 在 中, ,若 ,则 的形状为( )A、钝角三角形 B、等边三角形 C、直角三角形 D、不等边三角形3. 下列命题中,其逆命题是真命题的是( )A、对顶角相等 B、两直线平行,同位角相等 C、全等三角形的对应角相等 D、正方形的四个角都是直角4. 若 , 则下列不等式中正确的是( )A、 B、 C、 D、5. 如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )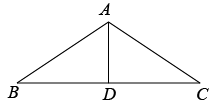 A、5 B、6 C、8 D、106. 如果方程组 的解与方程组 的解相同,则a+b的值为( )A、﹣1 B、1 C、2 D、07. 如图,将长方形沿折叠,使点B落到点处,交于点E,若 , 则等于( )
A、5 B、6 C、8 D、106. 如果方程组 的解与方程组 的解相同,则a+b的值为( )A、﹣1 B、1 C、2 D、07. 如图,将长方形沿折叠,使点B落到点处,交于点E,若 , 则等于( )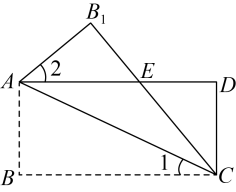 A、 B、 C、 D、8. 在平面直角坐标系中,若点在第二象限,则整数m的值为( )A、1 B、2 C、3 D、49. 若关于x的不等式2﹣m﹣x>0的正整数解共有3个,则m的取值范围是( )A、﹣1≤m<0 B、﹣1<m≤0 C、﹣2≤m<﹣1 D、﹣2<m≤﹣110. 如图,已知一次函数的图像经过点 , 则关于x的不等式的解集为( )
A、 B、 C、 D、8. 在平面直角坐标系中,若点在第二象限,则整数m的值为( )A、1 B、2 C、3 D、49. 若关于x的不等式2﹣m﹣x>0的正整数解共有3个,则m的取值范围是( )A、﹣1≤m<0 B、﹣1<m≤0 C、﹣2≤m<﹣1 D、﹣2<m≤﹣110. 如图,已知一次函数的图像经过点 , 则关于x的不等式的解集为( ) A、 B、 C、 D、11. 如图,在中,点F是边 , 的垂直平分线的交点,连接 , , 若 , 则等于( )
A、 B、 C、 D、11. 如图,在中,点F是边 , 的垂直平分线的交点,连接 , , 若 , 则等于( ) A、 B、 C、 D、12. 幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图(1)就是一个幻方.图(2)是一个未完成的幻方,则与的和是( )
A、 B、 C、 D、12. 幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图(1)就是一个幻方.图(2)是一个未完成的幻方,则与的和是( )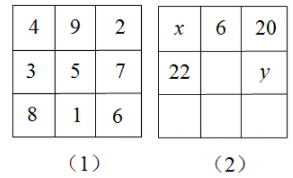 A、9 B、10 C、11 D、12
A、9 B、10 C、11 D、12二、填空题
-
13. 请你写一个成语,使成语所描述的事件是必然事件 .14. 将命题“相等的角是直角”改写成“如果……那么……”的形式 .15. 如果等腰三角形的一个外角为 , 那么它的顶角为 .16. 关于x的不等式组中的两个不等式的解集如图所示,则该不等式组的解集为 .
 17. 如图,在中,平分 , . 已知 , , 则的周长为 .
17. 如图,在中,平分 , . 已知 , , 则的周长为 . 18. 如果a,b满足则 .19. 将一箱书分给学生,若每位学生分6本书,则还剩10本书;若每位学生分8本书,则有一个学生分到书但不到4本.求这一箱书的本数与学生的人数.若设有学生x人,则列出的不等式组为 .20. 关于x的不等式组有且只有三个整数解,则a的最大值是 .
18. 如果a,b满足则 .19. 将一箱书分给学生,若每位学生分6本书,则还剩10本书;若每位学生分8本书,则有一个学生分到书但不到4本.求这一箱书的本数与学生的人数.若设有学生x人,则列出的不等式组为 .20. 关于x的不等式组有且只有三个整数解,则a的最大值是 .三、解答题
-
21.(1)、解不等式: , 并写出它的正整数解.(2)、如图,已知 , 于点D,于点E.

①求证:;
②若 , 求的度数.
(3)、求证:等腰三角形的底角必为锐角.22.(1)、在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.①先从袋子中取出个红球,再从袋子中随机摸出一个球,将“摸出黑球”记为事件A,请完成下列表格:
事件A
必然事件
随机事件
m的值
②先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率为 , 求m的值.
(2)、已知关于x,y的二元一次方程组的解x,y都正数,求m的取值范围.(3)、三个数在数轴上从左到右依次排列,试求a的取值范围.23. 已知:如图, , 和相交于点F.
求证:
(1)、;(2)、;(3)、 .24. 甲、乙两班学生到集市上购买苹果,价格如下:购买苹果数
不超过30千克
30千克以上但不超过50千克
50千克以上
每千克价格
3元
2.5元
2元
甲班分两次共购买苹果70千克(第二次多于第一次),共付出189元,而乙班则一次购买苹果70千克.
(1)、乙班比甲班少付出多少元?(2)、甲班第一次、第二次分别购买苹果多少千克?25. 小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形. (1)、问题发现:如图1,若△ABC和△ADE均是顶角为40°的等腰三角形,BC、DE分别是底边,求证:BD=CE;(2)、拓展探究:如图2,若△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE , 则∠AEB的度数为;线段BE与AD之间的数量关系是;(3)、解决问题:如图3,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CM为△DCE中DE边上的高,连接BE , 请判断∠AEB的度数及线段CM、AE、BE之间的数量关系并说明理由.
(1)、问题发现:如图1,若△ABC和△ADE均是顶角为40°的等腰三角形,BC、DE分别是底边,求证:BD=CE;(2)、拓展探究:如图2,若△ACB和△DCE均为等边三角形,点A、D、E在同一条直线上,连接BE , 则∠AEB的度数为;线段BE与AD之间的数量关系是;(3)、解决问题:如图3,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CM为△DCE中DE边上的高,连接BE , 请判断∠AEB的度数及线段CM、AE、BE之间的数量关系并说明理由.