四川省成都市金牛区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-12 类型:期末考试
一、单选题
-
1. 以下是某些运动会会标,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 纳米是一种长度单位,它用来表示微小的长度,1纳米为十亿分之一米,即米.甲型流感病毒的直径大约83纳米左右,“83纳米”用科学记数法表示为( )A、米 B、米 C、米 D、米4. 在△ABC中,∠A是钝角,下列图中画BC边上的高线正确的是( )A、
2. 下列运算正确的是( )A、 B、 C、 D、3. 纳米是一种长度单位,它用来表示微小的长度,1纳米为十亿分之一米,即米.甲型流感病毒的直径大约83纳米左右,“83纳米”用科学记数法表示为( )A、米 B、米 C、米 D、米4. 在△ABC中,∠A是钝角,下列图中画BC边上的高线正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 将一张长方形纸条按如图所示折叠,若 , 则的度数是( )
5. 将一张长方形纸条按如图所示折叠,若 , 则的度数是( ) A、 B、 C、 D、6. 下列事件中,属于必然事件的是( )A、两直线平行,同旁内角相等 B、过直线外一点有且只有一条直线与已知直线平行 C、有两边和一角相等的两个三角形一定全等 D、随意掷一枚质地均匀的骰子,掷出的点数是97. 如图,在和中,点E、F在上, , , 添加下列一个条件后能用“”判定的是( )
A、 B、 C、 D、6. 下列事件中,属于必然事件的是( )A、两直线平行,同旁内角相等 B、过直线外一点有且只有一条直线与已知直线平行 C、有两边和一角相等的两个三角形一定全等 D、随意掷一枚质地均匀的骰子,掷出的点数是97. 如图,在和中,点E、F在上, , , 添加下列一个条件后能用“”判定的是( ) A、 B、 C、 D、8. 在“爱成都•迎大运”手抄小报的活动中,小华立即开始办小报,抄了一段时间后因事暂停,过了一小会儿,小华继续抄写并加快了抄写速度,直至抄写完成,设从抄写文字开始所经过的时间为x,抄写字数为y,下面能反映y与x之间的关系的大致图象是( )A、
A、 B、 C、 D、8. 在“爱成都•迎大运”手抄小报的活动中,小华立即开始办小报,抄了一段时间后因事暂停,过了一小会儿,小华继续抄写并加快了抄写速度,直至抄写完成,设从抄写文字开始所经过的时间为x,抄写字数为y,下面能反映y与x之间的关系的大致图象是( )A、 B、
B、 C、
C、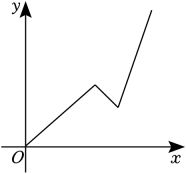 D、
D、
二、填空题
-
9. 已知 , 则 .10. 若多项式是一个关于x的完全平方式,则常数m的值为 .11. 一个锐角等于它的余角的2倍,那么这个锐角是12. 已知一个等腰三角形的周长为 , 底边的长为 , 则这个等腰三角形的腰长为 .13. 如图,在中, , 按以下步骤作图:
①以B为圆心,以任意长为半径作弧,分别交 , 于点M,N;
②分别以M、N为圆心,以大于的长为半径作弧,两弧在内交于点P;
③作射线 , 交于点D.若 , 则点D到直线的距离是 .

三、解答题
-
14. 计算下列各题:(1)、 .(2)、 .(3)、先化简,再求值: , 其中 .15. 某奶茶店销售奶茶的杯数x(杯)与销售总价y(元)的关系如下表:
奶茶数量x/杯
1
2
3
4
…
10
…
一销售总价y/元
12
22
32
42
…
102
…
(1)、写出销售总价y(元)与奶茶数量x(杯)的关系式.(2)、若该店想要在一天中销售总价达到822元,那么要销售多少杯奶茶?16. 一个口袋里装有红球12个,白球6个,这些球除颜色外完全相同,充分搅匀后随机摸出一球.(1)、摸到红球的概率是多少?(2)、从口袋中取出红球若干,搅匀后随机摸出一个球,摸到白球的概率为 , 则取出了多少个红球?17. 如图,方格纸中每个小方格都是边长为1的正方形,我们把顶点均在格点上的三角形称为“格点三角形”,如图,就是一个格点三角形. (1)、求的面积;(2)、作出关于直线m成轴对称的图形;(3)、利用网格在直线n上求作点P,使得是以为直角的直角三角形.(保留作图痕迹)18. 已知平分 , 如图1所示,点B在射线上,过点B作于点A,在射线上取一点C,使得 .
(1)、求的面积;(2)、作出关于直线m成轴对称的图形;(3)、利用网格在直线n上求作点P,使得是以为直角的直角三角形.(保留作图痕迹)18. 已知平分 , 如图1所示,点B在射线上,过点B作于点A,在射线上取一点C,使得 . (1)、若线段 , 求线段的长;(2)、如图2,点D是线段上一点,作 , 使得的另一边交于点E,连接 .
(1)、若线段 , 求线段的长;(2)、如图2,点D是线段上一点,作 , 使得的另一边交于点E,连接 .①是否成立,请说明理由;
②请判断三条线段的数量关系,并说明理由.
四、填空题
-
19. 已知 , 则 .20. 如图,直线 , 的平分线交直线于点D,若 , 则的度数为 .
 21. 已知中, , 若在五条线段中任选一条能作为边长的概率是 .22. 如图,锐角内有一定点A,连接 , 点B、C分别为、边上的动点,连接、、 , 设(),当取得最小值时,则 . (用含的代数式表示)
21. 已知中, , 若在五条线段中任选一条能作为边长的概率是 .22. 如图,锐角内有一定点A,连接 , 点B、C分别为、边上的动点,连接、、 , 设(),当取得最小值时,则 . (用含的代数式表示)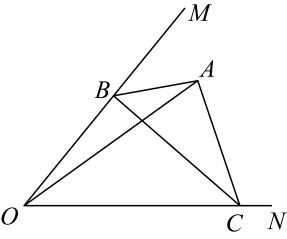 23. 已知和都是等腰三角形,且 , 顶角 , 等腰 的顶点D在边上滑动,点E在边的延长线上滑动.将线段绕点D逆时针旋转得到线段 , 连接 , 若是以为腰的等腰三角形,则 .
23. 已知和都是等腰三角形,且 , 顶角 , 等腰 的顶点D在边上滑动,点E在边的延长线上滑动.将线段绕点D逆时针旋转得到线段 , 连接 , 若是以为腰的等腰三角形,则 .
五、解答题
-
24. 已知 , .(1)、求的值;(2)、将长方形和长方形如图所示放置, , , 、的长分别为、的一半,求图中阴影部分的面积.
 25. 天府国际机场通航,负责机场货物装卸的某物流公司,现有甲、乙两条自动分拣流水线.已知甲运转1小时后,乙开始运转.如图所示,折线段、线段分别表示甲、乙两条流水线装卸货物的重量y(吨)与时间t(小时)之间的关系.其中,甲停转了2小时进行技术改进,改进后甲继续运转且流水线装卸效率与乙流水线相同;乙在运转了36分钟时,两条流水线装卸货物的重量相等.
25. 天府国际机场通航,负责机场货物装卸的某物流公司,现有甲、乙两条自动分拣流水线.已知甲运转1小时后,乙开始运转.如图所示,折线段、线段分别表示甲、乙两条流水线装卸货物的重量y(吨)与时间t(小时)之间的关系.其中,甲停转了2小时进行技术改进,改进后甲继续运转且流水线装卸效率与乙流水线相同;乙在运转了36分钟时,两条流水线装卸货物的重量相等.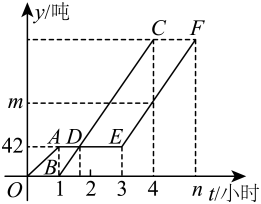 (1)、当时,甲装卸货物的重量y(吨)与时间t(小时)之间的关系式是;当时,乙装卸货物的重量y(吨)与时间(小时)之间的关系式是;(2)、求m和n的值;(3)、当时,甲、乙两条流水线装卸货物的重量相差35吨,求时间t的值.26. 已知等腰中, , 点D在射线上,连接 , 在右侧作等腰 , 且
(1)、当时,甲装卸货物的重量y(吨)与时间t(小时)之间的关系式是;当时,乙装卸货物的重量y(吨)与时间(小时)之间的关系式是;(2)、求m和n的值;(3)、当时,甲、乙两条流水线装卸货物的重量相差35吨,求时间t的值.26. 已知等腰中, , 点D在射线上,连接 , 在右侧作等腰 , 且 (1)、如图1,若平分 , 延长、交于点F,求证:;(2)、如图2,点M为的中点,求证:点M在线段的垂直平分线上;(3)、如图3,射线与射线交于点G,若 , 求的度数.
(1)、如图1,若平分 , 延长、交于点F,求证:;(2)、如图2,点M为的中点,求证:点M在线段的垂直平分线上;(3)、如图3,射线与射线交于点G,若 , 求的度数.