四川省成都市青羊区2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-07-12 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $∠ A = 25 °$ ，则它的余角是（　　）

A、 $25 °$ B、 $65 °$ C、 $115 °$ D、 $90 °$

查看试题解析
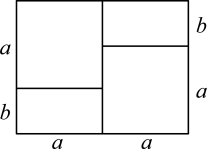
2. 成都大运会位于新津区的四川省水上运动学校赛艇场馆，与之配套的自动起航器设备起航反应时间小于 $0.09$ 秒，将 $0.09$ 用科学记数法表示应为（　　）

A、 $9 \times 1 0^{- 2}$ B、 $0.9 \times 1 0^{- 3}$ C、 $9 \times 1 0^{- 3}$ D、 $9 \times 1 0^{- 1}$

查看试题解析
3. 下列几何图形不一定是轴对称图形的是（　　）

A、线段 B、长方形 C、角 D、平行四边形

查看试题解析
4. 用三根长度分别为 $4 c m ， 5 c m ， 10 c m$ 的木条首尾顺次相接围成三角形，这属于（　　）

A、不可能事件 B、随机事件 C、必然事件 D、不确定事件

查看试题解析
5. 下列不能用平方差公式计算的是（　　）

A、 $(x + y) (x - y)$ B、 $(- x + y) (x - y)$ C、 $(- x + y) (- x - y)$ D、 $(- x + y) (x + y)$

查看试题解析
6. 某些代数恒等式可用几何图形的面积来验证，如图所示的几何图形的面积可验证的代数恒等式是（）

A、 $2 a (a + b) = 2 a^{2} + 2 a b$ B、 $2 a (2 a + b) = 4 a^{2} + 2 a b$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $(a + b) (a - b) = a^{2} - b^{2}$

查看试题解析
7. 用直尺和圆规作一个角的角平分线的示意图如图所示，其中说明 $Δ C O E ≅ Δ D O E$ 的依据是（）

A、 $S S S$ B、 $S A S$ C、 $A S A$ D、 $A A S$

查看试题解析
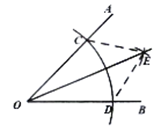8. 随着 $5 G$ 信号的快速发展， $5 G$ 无人物品派送车已应用于实际生活中，该车从出送点，在派送点停留一段时间后匀速返回出发位置，其行驶路程s与所用时间t的函数图象如图所示（不完整）．下列分析正确的是（　　）

A、派送车从出发点到派送点行驶的路程为 $1.6 k m$ B、在 $0 ～ 5 m i n$ 内，派送车的平均速度为 $0.12 k m / m i n$ C、在 $10 ～ 12 m i n$ 内，派送车在进行匀速运动 D、在 $5 ～ 11 m i n$ 内，派送车的速度逐渐增大

查看试题解析

二、填空题

9. 计算： $- 20 m^{6} \div 5 m^{2} =$ ．

查看试题解析
10. 在一周内，若小明同学饭卡原有200元．在校消费时间为周一到周五，平均每天在校消费36元，则他卡内余额y（单位：元）与在校天数x（x不大于5）（单位：天）之间的关系式为．

查看试题解析
11. 设计一个摸球游戏，先在一个不透明的盒子中放入2个白球，如果希望从中任意摸出1个球是白球的概率为 $\frac{1}{4}$ ，那么应该向盒子中再放入个其他颜色的球．（游戏用球除颜色外均相同）

查看试题解析
12. 如图， $△ A B C ≌ △ A D E$ ，若 $∠ C A E = 60 ° ， ∠ E = 70 °$ ，且 $A D ⊥ B C$ ，则 $∠ B A C$ 的度数为度．

查看试题解析
13. 如图，已知 $A$ 、 $B$ 、 $C$ 在同一条直线上，且 $∠ A = ∠ C = 52 °$ ， $A B = C E$ ， $A D = B C$ ，那么 $∠ B D E$ 的度数是度．

查看试题解析

三、解答题

14.

(1)、化简： ${(- x^{2})}^{3} + 2 x^{2} \cdot x^{4}$ ；

(2)、计算： $| - 3 | + (- 1^{2024}) \times (x - 3)^{0} + (- \frac{1}{2})^{- 3}$ ；

(3)、先化简，再求值： $5 x (x - 1) + {(2 x - 1)}^{2} - (3 x - 2) (3 x + 2)$ ，其中 $x = \frac{1}{3}$ ．

查看试题解析
15. “万里桥西一草堂，百花潭水即沧浪”，杜甫草堂的工作人员打算在A、B两点间建立一座观景桥，由于A、B中间隔着河流无法直接测量，数学兴趣小组想在不用涉水的情况下测量此段河流的宽度（该段河流两岸是平的），他们是这样做的：
①在河流的一条岸边B点，选对岸正对的一棵树A为参照点；
②沿河岸直走 $15 m$ 有一棵树C，继续前行 $15 m$ 到达D处；
③从D处沿河岸垂直的方向行走，当到达A树正好被C树遮挡住的E处停止行走；
④测得 $D E$ 的长为 $5 m$ ．

(1)、河流的宽度为 $m$ ；

(2)、请你证明他们做法的正确性．

查看试题解析
16. 如图在 $△ A B C$ 中，D是 $B C$ 边上的一点， $A B = D B$ ， $B E$ 平分 $∠ A B C$ ，交 $A C$ 边于点E，连接 $D E$ ．

(1)、求证： $△ A B E ≌ △ D B E$ ；

(2)、若 $∠ A = 100 ° ， ∠ C = 40 °$ ，求 $∠ D E C$ 的度数．

查看试题解析
17. 近年来，健身操《本草纲目》火爆全网，掀起全民健身热潮，为了解某中学学生对四种健身项目的喜爱情况，学校随机抽取了部分学生进行调查，将调查结果整理后绘制成如图两幅不完整的统计图，请结合图中提供的信息解答下列问题．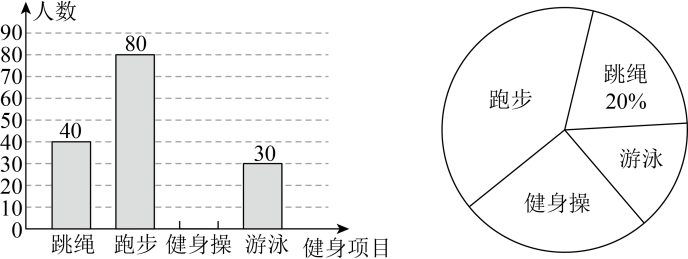

(1)、本次调查共调查了名学生，表示“跑步”的扇形圆心角度数为；

(2)、补全条形统计图；

(3)、若该校共有2000人，根据抽样调查结果，请估计全校喜爱“游泳”的学生人数．

查看试题解析
18. 如图，直线 $P Q ∥ M N$ ，一副三角板（ $∠ A B C = ∠ C D E = 90 °$ ， $∠ A C B = 30 °$ ， $∠ B A C = 60 °$ ， $∠ D C E = ∠ D E C = 45 °$ ）按如图①放置，其中点E在直线 $P Q$ 上，点B，C均在直线 $M N$ 上，且 $C E$ 平分 $∠ A C N$ ．

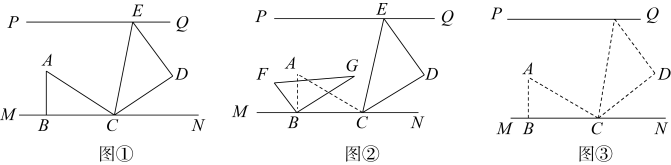(1)、求 $∠ D E Q$ 的度数；

(2)、如图②，若将 $△ A B C$ 绕B点以每秒5°的速度按逆时针方向旋转（A，C的对应点分别为F，G）．设旋转时间为t秒 $(0 \leq t \leq 36)$ ；
①在旋转过程中，若边 $B G ∥ C D$ ，求t的值；
②若在 $△ A B C$ 绕B点旋转的同时， $△ C D E$ 绕E点以每秒4°的速度按顺时针方向旋转．请直接写出旋转过程中 $△ C D E$ 有一边与 $B G$ 平行时t的值．

查看试题解析

四、填空题

19. 已知 $x^{2} - 2 x - 3 = 0$ ，则 $2 x^{2} - 4 x + 12 =$ ．

查看试题解析
20. 若 $x + m$ 与 $x^{2} + 2 x - 1$ 的乘积中不含 $x$ 的二次项，则实数 $m$ 的值为．

查看试题解析
21. 如图，在直角三角形 $A B C$ 中， $∠ C = 90 °$ ，点D在 $A B$ 上，点G在 $B C$ 上， $△ B D G$ 与 $△ F D G$ 关于直线 $D G$ 对称， $D F$ 与 $B$ 交于点E，若 $D F ∥ A C$ ， $∠ B = 28 °$ ，则 $∠ D G C$ 的度数是度．

查看试题解析
22. 如图，在长方形 $A B C D$ 中， $A B = 30$ ， $B C = 20$ ，点 $E$ ， $F$ 是 $B C$ 、 $C D$ 上的点，且 $B E = D F = x$ ，分别以 $F C$ 、 $C E$ 为边在长方形 $A B C D$ 外侧作正方形 $C F G H$ 和 $C E M N$ ，若长方形 $C E P F$ 的面积为 $220$ 平方单位，则图中阴影部分的面积和为平方单位．

查看试题解析
23. 如图，在三角形 $△ A B C$ 中， $∠ B A C = 46 °$ ， $A B = A C$ ， $B D ⊥ A C$ 于点 $D$ ， $M$ ， $N$ 分别是线段 $B D$ ， $B C$ 上的动点， $B M = C N$ ，当 $A M + A N$ 最小时， $∠ M A D =$ 度．

查看试题解析

五、解答题

24. 完全平方公式 ${(a + b)}^{2} = a^{2} \pm 2 a b + b^{2}$ 适当的变形，可以解决很多的数学问题．
请尝试解决：

(1)、若 $a + b = 5 ， a b = 2$ ，求 $a^{2} + b^{2}$ 的值；

(2)、若 $a + b = 10 ， a^{2} + b^{2} = 5 0^{2}$ ，求 $a b$ 的值．

查看试题解析
25. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．

大熊猫被誉为“中国国宝”，属于国家一级保护动物．为了更好地保护大熊猫，四川栗子坪自然保护区工作人员给大熊猫淘淘佩戴GPS颈圈监测它的活动规律．观测点A，B，C依次分布在一条直线上，观测点B距离A处 $150 m$ ，观测点C距离A处 $300 m$ ．监测人员发现淘淘某段时间内一直在A，B，C三个观测点之间活动，从A处匀速走到 $B$ 处，停留 $4 m i n$ 后，继续匀速走到C处，停留 $6 m i n$ 后，从C处匀速返回A处．给出的图象反映了淘淘在这段时间内离观测点A的距离 $y m$ 与离开观测点A的时间 $x m i n$ 之间的对应关系．

请根据相关信息，解答下列问题：

(1)、填表：
离开观测点A的时间 $/ m i n$
8
10
23
30
36
离观测点A的距离 $/ m$
60
240

(2)、填空：
①淘淘从观测点A到B的速度为 $m / m i n$
②观测点B与C之间的距离为 $m$ ；
③当淘淘离观测点A的距离为 $180 m$ 时，它离开观测点A的时间为 $m i n$ ．

(3)、当 $0 \leq x \leq 34$ 时，请直接写出 $y$ 关于 $x$ 的函数解析式．

查看试题解析
26. $△ A B C$ 中， $∠ A C B = 90 ° ， A C = B C$ ，点D是 $B C$ 边上的一个动点，连接 $A D$ 并延长，过点B作 $B F ⊥ A D$ 交 $A D$ 延长线于点F．

(1)、如图1，若 $A D$ 平分 $∠ B A C$ ， $A D = 6$ ，求 $B F$ 的值；

(2)、如图2，M是 $F B$ 延长线上一点，连接 $A M$ ，当 $A D$ 平分 $∠ M A C$ 时，试探究
$A C 、 C D 、 A M$ 之间的数量关系并说明理由；

(3)、如图3，连接 $C F$ ，
①求证： $∠ A F C = 45 °$ ；
② $S_{△ B C F} = \frac{35}{4}$ ， $S_{△ A C F} = 21$ ，求 $A F$ 的值．

查看试题解析

离开观测点A的时间 $/ m i n$	8	10	23	30	36
离观测点A的距离 $/ m$	60			240