四川省达州市达川区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-12 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 下列事件为必然事件的是( )A、一个三角形,其任意两边之和大于第三边 B、掷一枚质地均匀的骰子,掷出的点数是质数 C、一名射击运动员射击一次,中靶 D、彩票的中奖率是15%,那么买100张彩票必有15张中奖4. 一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如下数据:
2. 下列运算正确的是( )A、 B、 C、 D、3. 下列事件为必然事件的是( )A、一个三角形,其任意两边之和大于第三边 B、掷一枚质地均匀的骰子,掷出的点数是质数 C、一名射击运动员射击一次,中靶 D、彩票的中奖率是15%,那么买100张彩票必有15张中奖4. 一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如下数据:支撑物的高度
10
20
30
40
50
60
70
小车下滑的时间
下列说法正确的是( )
A、当时, B、随着h逐渐升高,t也逐渐变大 C、h每增加 , t减小 D、随着h逐渐升高,小车下滑的平均速度逐渐加快5. 如图,直线 , 被直线 , 所截,直线 , 下列结论中,不正确的是( ) A、 B、 C、 D、6. 如图,已知 , ,下列条件中,无法判定 的是( )
A、 B、 C、 D、6. 如图,已知 , ,下列条件中,无法判定 的是( ) A、 B、 C、 D、7. 如图,把一张长方形的纸片沿着折叠,点、分别落在、的位置,的延长线与交于点 , 若 , 则( )
A、 B、 C、 D、7. 如图,把一张长方形的纸片沿着折叠,点、分别落在、的位置,的延长线与交于点 , 若 , 则( ) A、 B、 C、 D、8. 如图,在长方形的中,已知 , , 点以的速度由点向点运动,同时点以的速度由点向点运动,若以 , , 为顶点的三角形和以 , , 为顶点的三角形全等,则的值为( )
A、 B、 C、 D、8. 如图,在长方形的中,已知 , , 点以的速度由点向点运动,同时点以的速度由点向点运动,若以 , , 为顶点的三角形和以 , , 为顶点的三角形全等,则的值为( ) A、 B、 C、或 D、或9. 如图,图1中的阴影部分移动成图2,根据两个图形中阴影部分的关系,可以验证下列哪个计算公式( )
A、 B、 C、或 D、或9. 如图,图1中的阴影部分移动成图2,根据两个图形中阴影部分的关系,可以验证下列哪个计算公式( )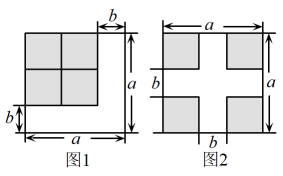 A、 B、 C、 D、10. 如图,在等边中,于D,延长到E,使 , F是的中点,连接并延长交于G,的垂直平分线分别交于点M,点N,连接 , , 下列结论:①;②;③;④ . 其中正确的结论序号是( ).
A、 B、 C、 D、10. 如图,在等边中,于D,延长到E,使 , F是的中点,连接并延长交于G,的垂直平分线分别交于点M,点N,连接 , , 下列结论:①;②;③;④ . 其中正确的结论序号是( ). A、①②③ B、②③④ C、①③④ D、①②③④
A、①②③ B、②③④ C、①③④ D、①②③④二、填空题
-
11. 如图,直线AB,CD相交于点O,OE⊥CD,垂足为点O,若∠BOE=40°,则∠AOC的度数为 .
 12. 有5张相同的卡片,卡片正面分别标有-2, , , , , 将卡片背面朝上,从中随机抽取1张,则抽取的卡片上的数是正数的概率为 .13. 已知 , 则 .14. 如图,把三角形纸片沿折叠,使点A落在四边形外部,已知 , , 则的度数为 .
12. 有5张相同的卡片,卡片正面分别标有-2, , , , , 将卡片背面朝上,从中随机抽取1张,则抽取的卡片上的数是正数的概率为 .13. 已知 , 则 .14. 如图,把三角形纸片沿折叠,使点A落在四边形外部,已知 , , 则的度数为 . 15. 如图,在中,D,E分别是的中点,点F在上,且 , 若 , 则等于 .
15. 如图,在中,D,E分别是的中点,点F在上,且 , 若 , 则等于 .
三、解答题
-
16. 计算:(1)、(2)、
四、解答题
-
17. 如图,已知 , , 下面求的度数,请填写推理的根据.

解:如图,过点E作 ,
∵(已知)
∴( )
∴( )
( )
∴( )
即
∴ .
18.(1)、化简求值 , 其中 .(2)、已知 , , 且的值不含a的一次项,求m的值.19. 如图,在正方形网格图中有一个 . (1)、画出关于直线的对称图形(不写画法);(2)、若网格上的每个小正方形的边长为1,求的面积.20. 2022年3月23日,“天宫课堂”第二课在中国空间站正式开讲,航天员王亚平、叶光富、翟志刚为学生们上了一堂豪华的太空课,引发了学生了解科学知识的新热潮.八(1)班社团通过查阅资料发现,声音在空气中传播的速度和气温的变化存在如下的关系:
(1)、画出关于直线的对称图形(不写画法);(2)、若网格上的每个小正方形的边长为1,求的面积.20. 2022年3月23日,“天宫课堂”第二课在中国空间站正式开讲,航天员王亚平、叶光富、翟志刚为学生们上了一堂豪华的太空课,引发了学生了解科学知识的新热潮.八(1)班社团通过查阅资料发现,声音在空气中传播的速度和气温的变化存在如下的关系:气温
0
5
10
15
20
25
声音在空气中的传播速度
331
334
337
340
343
346
(1)、在这个变化过程中,是自变量,是因变量.(2)、从表中数据可知,气温每升高1℃,声音在空气中传播的速度就提高m/s.(3)、声音在空气中的传播速度与气温t(℃)的关系式可以表示为;(4)、某日的气温为22℃,小乐看到烟花燃放5s后才听到声响,那么小乐与燃放烟花所在地大约相距多远?21. 2022年“新课标”提出,义务教育劳动课程以丰富开放的劳动项目为载体.南开中学积极发挥劳动教育的融合性特征,从课程设计、课余生活等多维度,鼓励学生积极参与劳动.为了解七年级学生一周参与劳动时间的情况,随机抽取部分学生,统计了他们每周劳动时间(单位:h),并将收集到的数据整理分析,共分为五组:(A:x<1,B:1≤x<2,C:2≤x<3,D:3≤x<4,E:x≥4,其中每周劳动时间不少于3小时为达标),绘制了如下两幅不完整的统计图:
结合图中提供的信息,解答下列问题:
(1)、本次调查的总人数为人,a=;(2)、把频数分布直方图补充完整;(3)、为了让全校学生重视劳动学习,学校准备从这些达标学生中随机抽取1名学生给全校学生分享劳动收获心得,若已知在这些达标学生中有男生13人,求抽中女生的概率.22. 如图,在和中, , , 在的延长线上取点 , 使 , 连接 . (1)、试说明:;(2)、连接交于点 , 若 , , 试说明: .23. 图1是一个长为 , 宽为的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图2拼成一个正方形.
(1)、试说明:;(2)、连接交于点 , 若 , , 试说明: .23. 图1是一个长为 , 宽为的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图2拼成一个正方形. (1)、观察图2,请直接写出代数式 , , 之间的等量关系;(2)、根据(1)中的等量关系,若 , , 则的值为;(3)、已知 , 求的值.24. 已知 .
(1)、观察图2,请直接写出代数式 , , 之间的等量关系;(2)、根据(1)中的等量关系,若 , , 则的值为;(3)、已知 , 求的值.24. 已知 . (1)、如图1,按如下要求用尺规作图:
(1)、如图1,按如下要求用尺规作图:①作出的中线;
②延长至E,使 , 连接;(不要求写出作法,但要保留作图痕迹.)
(2)、如图2,若是中线.试探究与之间的数量关系,并说明理由;(3)、如图3,若是的中线,过点B作于E,交于点F,连接 . 若 , 求的长.25. 如图,在中, , , 边沿着过点的某条直线对折得到 , 连接 , 以为边在左侧作 , 其中 , , 与交于点 , 连接 .(1)、如图1,连接 , 当点在外部时,试说明; (2)、如图2,连接 , 当点在的斜边上时,试判断的形状并说明理由;
(2)、如图2,连接 , 当点在的斜边上时,试判断的形状并说明理由; (3)、如图3,当点在的内部时,若点为的中点,且 , 求的长.
(3)、如图3,当点在的内部时,若点为的中点,且 , 求的长.
-