重庆市江津区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-12 类型:期末考试
一、单选题
-
1. 下列实数中,是无理数的是( )A、 B、 C、 D、2. 已知点P位于第四象限,则点P的坐标可能是( )A、 B、 C、 D、3. 已知 , 则下列不等式不一定成立的是( )A、 B、 C、 D、4. 如图,请你从下面选项中选出能证明的是( )
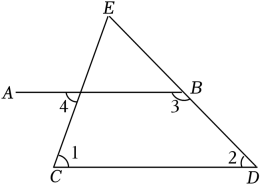 A、 B、 C、 D、5. 估计的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间6. 下列命题正确的是( )A、所有实数不是正数就是负数 B、相等的角是对顶角 C、如果 , 那么 D、同一平面内,如果 , , 那么7. 随着中体考改革,对学生身体素质要求越来越高.为了解某校学生周末体育锻炼时长的情况,随机抽查了其中60名学生进行统计,并绘制成如图所示的频数分布直方图,已知该校共有720名学生,据此估计,该校学生周末体育锻炼时间在小时之间的学生数大约是( )
A、 B、 C、 D、5. 估计的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间6. 下列命题正确的是( )A、所有实数不是正数就是负数 B、相等的角是对顶角 C、如果 , 那么 D、同一平面内,如果 , , 那么7. 随着中体考改革,对学生身体素质要求越来越高.为了解某校学生周末体育锻炼时长的情况,随机抽查了其中60名学生进行统计,并绘制成如图所示的频数分布直方图,已知该校共有720名学生,据此估计,该校学生周末体育锻炼时间在小时之间的学生数大约是( )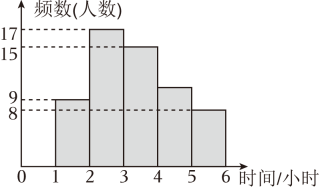 A、122 B、130 C、132 D、1408. 《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”译文:“几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价格是多少?”设有x人,物品价格为y钱,可列方程组为( )A、 B、 C、 D、9. 如图,动点A在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点 , 第二次运动到点 , 第三次运动到 , …,按这样的运动规律,第23次运动后,动点的坐标是( )
A、122 B、130 C、132 D、1408. 《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”译文:“几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价格是多少?”设有x人,物品价格为y钱,可列方程组为( )A、 B、 C、 D、9. 如图,动点A在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点 , 第二次运动到点 , 第三次运动到 , …,按这样的运动规律,第23次运动后,动点的坐标是( )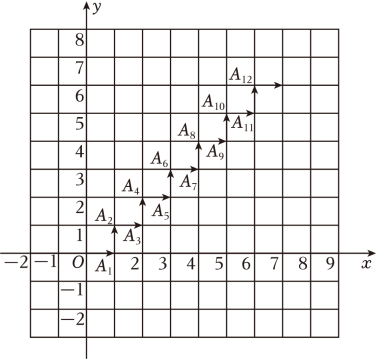 A、 B、 C、 D、10. 对a、b定义一种新运算T,规定: , 这里等式右边是通常的四则运算.例如: , 则下列结论正确的个数为( )
A、 B、 C、 D、10. 对a、b定义一种新运算T,规定: , 这里等式右边是通常的四则运算.例如: , 则下列结论正确的个数为( )①;②若 , 则;③若 , 则;④若 , 则m、n有且仅有6组整数解.
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 5的平方根是 .
12. 为了了解“双减”背景下全国中小学生完成课后作业的时间情况,比较适合的调查方式是(填“全面调查”或“抽样调查”).13. 已知点在x轴上,则点M的坐标是 .14. 已知是关于x的一元一次不等式,则 .15. 已知是二元一次方程组的解,则的算术平方根为 .16. 如图,直线 , 直线c与直线a,b分别交于点E、F,射线直线c,若 , 则的度数是 .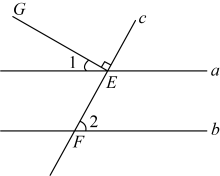 17. 若关于x的不等式组的解集是 , 且关于y、z的二元一次方程组的解满足 , 则所有满足条件的整数a的值之和为 .18. 对于一个三位数m,若其各个数位上的数字都不为0且互不相等,则称这样的数为“快乐数”.将“快乐数”m任意两个数位上的数字取出组成两位数,则一共可以得到6个两位数,将这6个两位数的和记为 . 例如, . 记 , 则 , 若“快乐数”m满足百位上的数字是个位上数字的2倍,且能被7整除,求满足条件的“快乐数”m的最大值为 .
17. 若关于x的不等式组的解集是 , 且关于y、z的二元一次方程组的解满足 , 则所有满足条件的整数a的值之和为 .18. 对于一个三位数m,若其各个数位上的数字都不为0且互不相等,则称这样的数为“快乐数”.将“快乐数”m任意两个数位上的数字取出组成两位数,则一共可以得到6个两位数,将这6个两位数的和记为 . 例如, . 记 , 则 , 若“快乐数”m满足百位上的数字是个位上数字的2倍,且能被7整除,求满足条件的“快乐数”m的最大值为 .三、解答题
-
19. 计算:(1)、;(2)、 .20.(1)、解方程组:;(2)、解不等式组 , 并将其解集表示在数轴上.
 21. 如图, , 点E、F分别在、上,连接 , 和 , 和相交于H, , , 求证: .
21. 如图, , 点E、F分别在、上,连接 , 和 , 和相交于H, , , 求证: .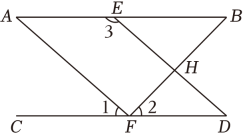
证明:∵ ,
∴ , ( )
∵ ,
∴(等量代换),
∵ ,
∴ ▲ ② ,
又∵ , ,
∴ ▲ ③(等量代换),
∴( ),
∴ ▲ ⑤(两直线平行,同位角相等),
∴(垂直的定义).
22. 某校七年级学生们在老师的组织下,就近期人们比较关注的五个话题:A.5G通信技术;B.北斗导航;C.数字经济;D.民法典;E.人工智能,对校外某小区居民进行了随机抽样调查,每人只能从中选择一个本人最关注的话题,根据调查结果绘制了如图两幅不完整的统计图.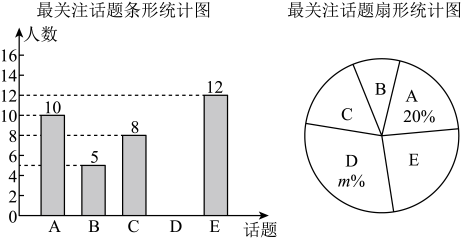
请结合统计图中的信息,解决下列问题:
(1)、七年级学生们在这次活动中,调查的居民共有 人;请补全条形统计图;(2)、最关注话题扇形统计图中的m= , 话题D所在扇形的圆心角是度;(3)、假设这个小区居民共有3500人,请估计该小区居民中最关注的话题是“人工智能”的人数大约有多少?23. 如图,已知三角形三个顶点的坐标分别是 , , , 将三角形进行平移后,三角形内任一点的对应点为 .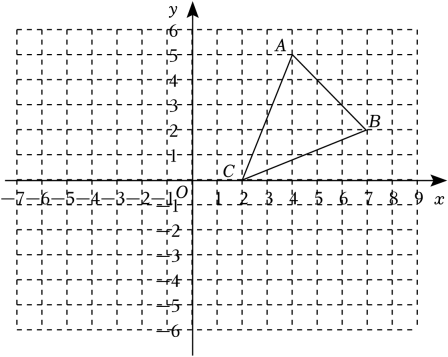 (1)、画出平移后的三角形;(2)、写出 , , 的坐标;(3)、求三角形的面积.24. 大数据显示,新能源汽车需求量正倍速的增长.为满足客户需求,现某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解1辆A型汽车、2辆B型汽车的进价共计75万元;2辆A型汽车、3辆B型汽车的进价共计130万元.(1)、求A、B两种型号的汽车每辆进价分别为多少万元?(2)、若该公司计划以不超过300万元购进以上两种型号的新能源汽车共10辆,并且该汽车销售公司销售1辆A型汽辆车可获利8000元,销售1辆B型汽车可获利5000元,假如这些新能源汽车全部售出,至少要获得62000元的利润,该公司有哪几种购进方案?哪种方案获得的利润最多,最多利润是多少?25. 如图,在平面直角坐标系中,长方形的顶点A、C分别在x轴、y轴上,轴,轴,点B的坐标为 , 且 .
(1)、画出平移后的三角形;(2)、写出 , , 的坐标;(3)、求三角形的面积.24. 大数据显示,新能源汽车需求量正倍速的增长.为满足客户需求,现某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解1辆A型汽车、2辆B型汽车的进价共计75万元;2辆A型汽车、3辆B型汽车的进价共计130万元.(1)、求A、B两种型号的汽车每辆进价分别为多少万元?(2)、若该公司计划以不超过300万元购进以上两种型号的新能源汽车共10辆,并且该汽车销售公司销售1辆A型汽辆车可获利8000元,销售1辆B型汽车可获利5000元,假如这些新能源汽车全部售出,至少要获得62000元的利润,该公司有哪几种购进方案?哪种方案获得的利润最多,最多利润是多少?25. 如图,在平面直角坐标系中,长方形的顶点A、C分别在x轴、y轴上,轴,轴,点B的坐标为 , 且 .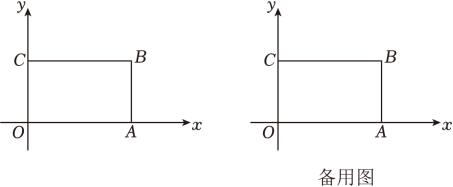 (1)、请直接写出点A、B、C的坐标;(2)、若动点P从原点O出发,沿y轴以每秒1个长度单位的速度向上运动,在运动过程中形成的三角形的面积是长方形面积的时,点停止运动,求点P的运动时间;(3)、在(2)的条件下,在x轴上是否存在一点Q,使三角形的面积与长方形的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.26. 如图1,直线 , 点M、N分别在上,点P为平行线内部一点,连接 .
(1)、请直接写出点A、B、C的坐标;(2)、若动点P从原点O出发,沿y轴以每秒1个长度单位的速度向上运动,在运动过程中形成的三角形的面积是长方形面积的时,点停止运动,求点P的运动时间;(3)、在(2)的条件下,在x轴上是否存在一点Q,使三角形的面积与长方形的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.26. 如图1,直线 , 点M、N分别在上,点P为平行线内部一点,连接 .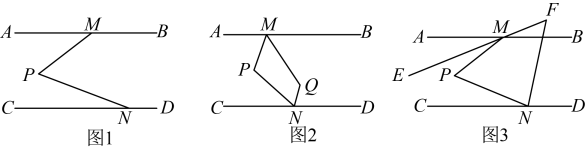 (1)、若 , 求的度数;(2)、如图2,平分 , 平分 , 与相交于点Q,求证:;(3)、如图3,作平分 , 平分 , 反向延长交于点F,请直接写出与之间的数量关系.
(1)、若 , 求的度数;(2)、如图2,平分 , 平分 , 与相交于点Q,求证:;(3)、如图3,作平分 , 平分 , 反向延长交于点F,请直接写出与之间的数量关系.