2023年浙教版数学七年级上册1.2 数轴 同步测试（培优版）
试卷更新日期：2023-07-12 类型：同步测试
一、选择题（每题2分，共20分）
-
1. 如图，数轴的单位长度为1，数轴上有A，B，C三个点．若点A，B到原点的距离相等，则点C表示的数是（ ）
A、2 B、1 C、−1 D、−22. 小明在写作业时不慎将两滴墨水滴在数轴上，如图所示，此时墨迹盖住的整数共有（ ）个．
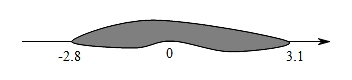A、3 B、4 C、5 D、63. 如图，数轴上有三个点A，B，C，若点A，B表示的数互为相反数，且 ， 则点C表示的数是（ ）
A、6 B、4 C、2 D、04. 点A、B是数轴上的两点，分别表示、 ， 把线段沿数轴向右移动到 ， 且线段的中点对应的数是2，则点对应的数是（ ）A、0 B、 C、 D、5. 如图，将一刻度尺放在数轴上，（数轴的单位长度是），刻度尺上对应数轴上的数3，那么数轴上-2.5对应刻度尺上的数字为：（ ）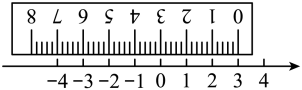
A、5.3 B、5.5 C、-5.5 D、66. 一电子跳蚤落在数轴上的某点k0处，第一步从k0向左跳一个单位到k1 ， 第二步从k1向右跳2个单位到k2 ， 第三步由k2处向左跳3个单位到k3 ， 第四步由k3向右跳4个单位k4 ， ….按以上规律跳了100步后，电子跳蚤落在数轴上的数是0，则k0表示的数是A、0 B、100 C、50 D、7. 如图，圆的周长为4个单位长度．在该圆的4等分点处分别标上0、1、2、3，先让圆周上表示数字0的点与数轴上表示-1的点重合，再将数轴按逆时针方向环绕在该圆上．则数轴上表示2013的点与圆周上表示数字（ ）的点重合．
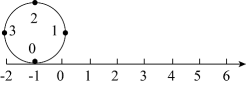A、0 B、1 C、2 D、38. 数轴上表示整数的点称为整点，某数轴的单位长度为1cm ， 若在数轴上画出一条长2020cm的线段AB ， 则线段AB盖住的整点个数是（ ）A、2020 B、2021 C、2020或2021 D、2019或20209. 点A，B是数轴上两点，位置如图，点P，Q是数轴上两动点，点P由点A点出发，以1单位长度/秒的速度在数轴上运动，点Q由点B点出发，以2单位长度/秒的速度在数轴上运动．若两点同时开始和结束运动，设运动时间为t秒．下面是四位同学的判断：①小康同学：当t=2时，点P和点Q重合．
②小柔同学：当t=6时，点P和点Q重合．
③小议同学：当t=2时，PQ=8．
④小科同学：当t=6时，PQ=18．
以上说法可能正确的是（ ）
A、①②③ B、②③④ C、①③④ D、①②③④10. 如图，一个动点从原点 开始向左运动，每秒运动1个单位长度，并且规定：每向左运动3秒就向右运动2秒，则该动点运动到第2021秒时所对应的数是（ ）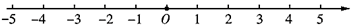
A、-406 B、-405 C、-2020 D、-2021二、填空题（每空3分，共24分）
-
11. 如图，图中数轴的单位长度为1，点A，B所表示的数互为相反数，若点M为线段中点，则点M所表示的数为.
12. 一滴墨水洒在一个数轴上，根据图中标出的数值，判断墨迩盂住的整数个数是。
13. 若表示互为相反数的两个数的点A、B在数轴上的距离为10个单位长度，点A沿数轴先向右运动2秒，再向左运动5秒到达点C，设点A的运动速度为每秒2个单位长度，则点C在数轴上表示的数的为14. 如图，正方体纸盒上相对两个面上的数互为相反数，则正方体纸盒六个面上的数中，最小的是 ．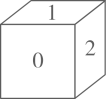
15. 探究思考：（本题直接填空，不必写出解题过程）问题：在数轴上，点A表示的数为 ，则到点A的距离等于3的点所表示的数是；
变式思考一：如图1，在数轴上有六个点A、B、C、D、E、F ， 且相邻两点间距离相等，若点A表示的数是 ，点F表示的数为11，则与点C表示的数最近的整数是；
变式思考二：已知数轴上有A、B、C三点，分别代表 ，电子蚂蚁从A向点C方向以4个单位/秒的速度爬行.则爬行到秒时，电子蚂蚁到A、B、C的距离和为40个单位.
16. 电影《哈利•波特》中，小哈利波特穿越墙进入“ 站台”的镜头（如示意图的Q站台），构思奇妙，能给观众留下深刻的印象．若A、B站台分别位于﹣ ， 处，AP=2PB，则P站台用类似电影的方法可称为“站台”．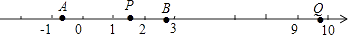
三、解答题（共8题，共76分）
-
17. 甲、乙两队进行拔河比赛，标志物先向乙队方向移动了0.2米，又向甲队方向移动了0.6米．相持一会儿后，标志物向乙队方向移动了0.5米，随后又向甲队方向移动了1.3米，在大家的加油声中，标志物又向甲队方向移动了0.9米．若规定标志物向某队方向移动2米以上该队即可获胜，通过计算说明最后哪队获胜？18. 如图所示，一个点从数轴上的原点开始，先向右移动3单位长度，再向左移动5个单位长度，可以看到终点表示的数是﹣2，已知点A，B是数轴上的点，请参照下图并思考，完成下列各题．
(1)、如果点A表示数-3，将A点向右移动7个单位长度，那么终点B表示的数是 ， A，B两点间的距离为 ．(2)、如果点A表示数3，将A点向左移动7个单位长度，再向右移动5个单位长度，那么终点B表示的数是 ， A，B两点间的距离为 ．(3)、如果点A表示数-4，将A点向右移动168个单位长度，再向左移动256个单位长度，那么终点B表示的数是 ， A，B两点间的距离是 ．(4)、一般地，如果A点表示数为m，将A点向右移动n个单位长度，再向左移动P个单位长度，那么，请你猜想终点B表示什么数？A，B两点间的距离为多少？19. 问题探索：如图，将一根木棒放在数轴（单位长度为1cm）上，木棒左端与数轴上的点A重合，右端与数轴上的点B重合.
(1)、若将木棒沿数轴向右水平移动，则当它的左端移动到点B时，它的右端在数轴上所对应的数为30；若将木棒沿数轴向左水平移动，则当它的右端移动到点A时，它的左端在数轴上所对应的数为6，由此可得这根木棒的长为cm.(2)、图中点A所表示的数是 ， 点B所表示的数是.(3)、实际应用：由（1）（2）的启发，请借助“数轴”这个工具解决下列问题：一天，妙妙去问奶奶的年龄，奶奶说：“我若是你现在这么大，你还要32年才出生；你若是我现在这么大，我就106岁啦！”请问妙妙现在多少岁了？20. 小强早晨跑步，他从自己家出发，向东跑了2km到达小兵家，继续向东跑了1.5km到达小颖家，然后又向西跑了4.5km到达学校，最后又向东跑回到自己家．(1)、以小强家为原点，向东为正方向，用1个单位长度表示1km，在图中的数轴上，分别用点A表示出小兵家，用点B表示出小颖家，用点C表示出学校的位置；
(2)、求小兵家与学校之间的距离；(3)、如果小强跑步的速度是250 ， 那么小强跑步一共用了多长时间？21. 点O为数轴的原点，点A，B在数轴上的位置如图所示，点B表示的数为4，线段的长为线段长的1.5倍.点C在数轴上，M为线段的中点.
(1)、点A表示的数为；(2)、若线段 ， 则线段的长为；(3)、若线段（），求线段的长（用含a的式子表示）.22. 操作与探究：已知在纸面上有数轴 （如图），折叠纸面．
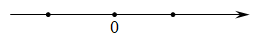
例如：若数轴上数3表示的点与数－3表示的点重合，则数轴上数－5表示的点与数5表示的点重合，根据你对例题的理解，解答下列问题：
(1)、若数轴上数2表示的点与－2表示的点重合，则数轴上数7表示的点与数表示的点重合．(2)、若数轴上数－5表示的点与数1表示的点重合．①则数轴上数3表示的点与数重合．
②若数轴上A，B两点之间的距离为10（A在B的左侧），并且A，B两点经折叠后重合，则A，B两点表示的数分别是 ， ．
23. 如图，相距5km的A、B两地间有一条笔直的马路，C地位于AB两地之间且距A地2km，小明同学骑自行车从A地出发沿马路以每小时5km的速度向B地匀速运动，当到达B地后立即以原来的速度返回.到达A地停止运动，设运动时间为t(小时).小明的位置为点P、若以点C为坐标原点，以从A到B为正方向，用1个单位长度表示1km，解答下列各问：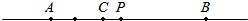
(1)、指出点A所表示的有理数；(2)、求t =0.5时，点P表示的有理数；(3)、当小明距离C地1km时，直接写出所有满足条件的t值；(4)、在整个运动过程中，求点P与点A的距离(用含t的代数式表示)；(5)、用含t的代数式表示点P表示的有理数.24. 定义：若A，B，C为数轴上三点，若点C到点A的距离是点C到点B的距离2倍，我们就点C是(A，B)的美好点例如：如图1，点A表示的数为-1，点B表示的数为2.表示1的点C到点A的距离是2，到点B的距离是1，那么点C是(A，B)的美好点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D就不是〔A，B)的美好点，但点D是(B，A)的美好点。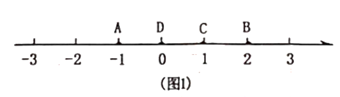
如图2，M，N为数轴上两点，点M所表示的数为-7，点N所表示的数为2.
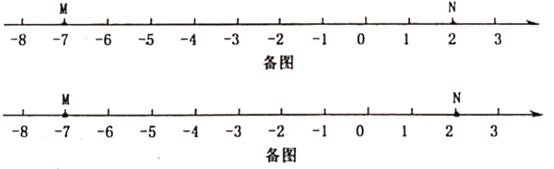(1)、点E，F，G表示的数分别是-3，6.5，11，其中是(M，N)美好点的是； 写出(N，M)美好点H所表示的数是。(2)、现有一只电子蚂蚁P从点N开始出发，以2个单位每秒的速度向左运动.当t为何值时，P，M和N中恰有一个点为其余两点的美好点?