北师大版数学九年级上册同步练习——第一章《特殊平行四边形》综合练习
试卷更新日期:2023-07-11 类型:单元试卷
一、选择题
-
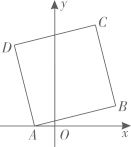
1. 下列命题正确的是( )A、正方形的对角线相等且互相平分 B、对角互补的四边形是平行四边形 C、矩形的对角线互相垂直 D、一组邻边相等的四边形是菱形2. 如图,在平行四边形中, , , 将线段水平向右平移a个单位长度得到线段 , 若四边形为菱形时,则a的值为( )
 A、1 B、2 C、3 D、43. 如图,▱ABCD的对角线AC和BD相交于点O,下列说法正确的是( )
A、1 B、2 C、3 D、43. 如图,▱ABCD的对角线AC和BD相交于点O,下列说法正确的是( )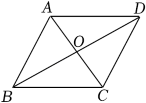 A、若OB=OD,则▱ABCD是菱形 B、若AC=BD,则▱ABCD是菱形 C、若OA=OD,则▱ABCD是菱形 D、若AC⊥BD,则▱ABCD是菱形4. 如图,在菱形纸片ABCD中,E是BC边上一点,将△ABE沿直线AE翻折,使点B落在上,连接 . 已知∠C=120°,∠BAE=50°,则的度数为( )
A、若OB=OD,则▱ABCD是菱形 B、若AC=BD,则▱ABCD是菱形 C、若OA=OD,则▱ABCD是菱形 D、若AC⊥BD,则▱ABCD是菱形4. 如图,在菱形纸片ABCD中,E是BC边上一点,将△ABE沿直线AE翻折,使点B落在上,连接 . 已知∠C=120°,∠BAE=50°,则的度数为( )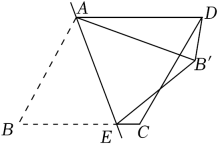 A、50° B、60° C、80° D、90°5. 如图,矩形ABCD为一个正在倒水的水杯的截面图,杯中水面与CD的交点为E,当水杯底面BC与水平面的夹角为27°时,∠AED的大小为( )
A、50° B、60° C、80° D、90°5. 如图,矩形ABCD为一个正在倒水的水杯的截面图,杯中水面与CD的交点为E,当水杯底面BC与水平面的夹角为27°时,∠AED的大小为( ) A、27° B、53° C、57° D、63°6. 如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,AH=CF,AE=CG,∠EHF=60°,∠GHF=45°.若AH=2,AD=5+ . 则四边形EFGH的周长为( )
A、27° B、53° C、57° D、63°6. 如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,AH=CF,AE=CG,∠EHF=60°,∠GHF=45°.若AH=2,AD=5+ . 则四边形EFGH的周长为( )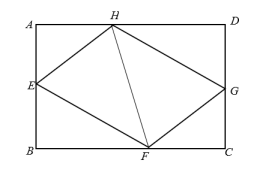 A、 B、 C、 D、7. 如图,矩形ABCD中,分别以A,C为圆心,以大于的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AD,BC于点E,F,连接AF,若BF=3,AE=5,以下结论错误的是( )
A、 B、 C、 D、7. 如图,矩形ABCD中,分别以A,C为圆心,以大于的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AD,BC于点E,F,连接AF,若BF=3,AE=5,以下结论错误的是( )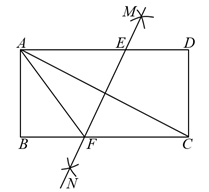 A、AF=CF B、∠FAC=∠EAC C、AB=4 D、AC=2AB8. 如图,在边长为4的菱形ABCD中,E为AD边的中点,连接CE交对角线BD于点F.若∠DEF=∠DFE,则这个菱形的面积为( )
A、AF=CF B、∠FAC=∠EAC C、AB=4 D、AC=2AB8. 如图,在边长为4的菱形ABCD中,E为AD边的中点,连接CE交对角线BD于点F.若∠DEF=∠DFE,则这个菱形的面积为( )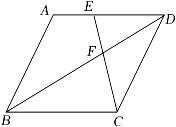 A、16 B、6 C、12 D、309. 如图,菱形 ABCD 对角线交点与坐标原点 O 重合,点 A(-2,5) ,则点C的坐标为( )
A、16 B、6 C、12 D、309. 如图,菱形 ABCD 对角线交点与坐标原点 O 重合,点 A(-2,5) ,则点C的坐标为( )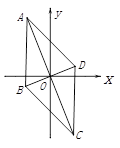 A、 B、 C、 D、10. 如图,在正方形 ABCD 中,对角线 AC,BD 相交于点 O.E,F 分别为 AC,BD 上一点,且 OE=OF,连接 AF,BE,EF,若∠AFE=25°,则∠CBE 的度数为( )
A、 B、 C、 D、10. 如图,在正方形 ABCD 中,对角线 AC,BD 相交于点 O.E,F 分别为 AC,BD 上一点,且 OE=OF,连接 AF,BE,EF,若∠AFE=25°,则∠CBE 的度数为( ) A、50° B、55° C、65° D、70°11. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,OH=4,若菱形ABCD的面积为32 , 则CD的长为( )
A、50° B、55° C、65° D、70°11. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,OH=4,若菱形ABCD的面积为32 , 则CD的长为( )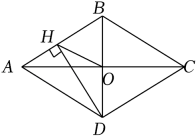 A、4 B、4 C、8 D、812. 如图,在菱形ABCD中, , M是对角线BD上的一个动点, , 则的最小值为( )
A、4 B、4 C、8 D、812. 如图,在菱形ABCD中, , M是对角线BD上的一个动点, , 则的最小值为( )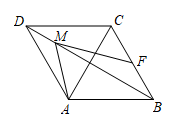 A、1 B、 C、 D、2
A、1 B、 C、 D、2二、填空题
-
13. 矩形纸片ABCD中, , , 点M在AD边所在的直线上,且 , 将矩形纸片ABCD折叠,使点B与点M重合,折痕与AD,BC分别交于点E,F,则线段EF的长度为.14. 在平面直角坐标系中,正方形如图所示,点的坐标 , 点的坐标是 , 则点的坐标是 .
 15. 如图,将矩形纸片ABCD沿CE折叠,使点B落在边AD上的点F处.若点E在边AB上,AB=3,BC=5,则AE= .
15. 如图,将矩形纸片ABCD沿CE折叠,使点B落在边AD上的点F处.若点E在边AB上,AB=3,BC=5,则AE= .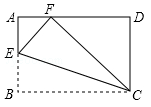 16. 如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A′满足AA′=AC,则所得正方形与原正方形重叠部分的面积是 .
16. 如图,将边长为3的正方形ABCD沿其对角线AC平移,使A的对应点A′满足AA′=AC,则所得正方形与原正方形重叠部分的面积是 .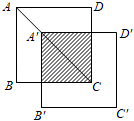 17. 矩形ABCD中, , , 点E在AB边上, . 若点P是矩形ABCD边上一点,且与点A,E构成以AE为腰的等腰三角形,则等腰三角形AEP的底边长是 .18. 如图,矩形 中, , 是 的中点,线段 在边 上左右滑动;若 ,则 的最小值为 .
17. 矩形ABCD中, , , 点E在AB边上, . 若点P是矩形ABCD边上一点,且与点A,E构成以AE为腰的等腰三角形,则等腰三角形AEP的底边长是 .18. 如图,矩形 中, , 是 的中点,线段 在边 上左右滑动;若 ,则 的最小值为 .
三、解答题
-
19. 如图,点E,F分别在正方形ABCD的边BC,CD上,且 . 把绕点A顺时针旋转得到 . 求证: .
 20. 如图所示,平行四边形对角线交于点O,过点O作分别交于F,E两点,求证四边形为菱形.
20. 如图所示,平行四边形对角线交于点O,过点O作分别交于F,E两点,求证四边形为菱形.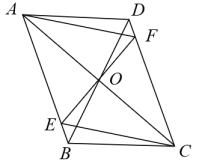 21. 【阅读材料】
21. 【阅读材料】老师的问题:
已知:如图, .
求作:菱形 , 使点C,D分别在上.
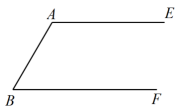
小明的作法:
(1)以A为圆心,长为半径画弧,交于点D;
(2)以B为圆心,长为半经画弧,交于点C;
(3)连接 .
四边形就是所求作的菱形,
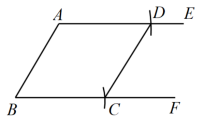
【解答问题】
请根据材料中的信息,证明四边形是菱形.
22. 如图,在中,D是的中点,E是的中点,过点A作交的延长线于点F.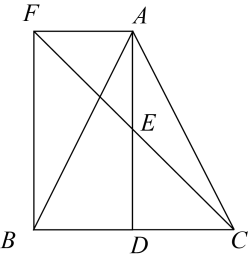 (1)、求证:;(2)、连接 , 若 , 求证:四边形是矩形.
(1)、求证:;(2)、连接 , 若 , 求证:四边形是矩形.


