北师大版数学九年级上册同步练习——第一章《特殊平行四边形》3.正方形的性质与判定(2)
试卷更新日期:2023-07-11 类型:同步测试
一、选择题
-
1. 下列命题是真命题的是( )A、对边相等的四边形是平行四边形 B、有一个角是90°的平行四边形是矩形 C、邻边相等的四边形是菱形 D、对角线互相垂直的平行四边形为正方形2. 如图推理中,空格①②③④处可以填上条件“对角线相等”的是( )
 A、①② B、①④ C、③④ D、②③3. 如图,在矩形中,对角线交于点O,下列条件中,能使矩形成为正方形的是( )
A、①② B、①④ C、③④ D、②③3. 如图,在矩形中,对角线交于点O,下列条件中,能使矩形成为正方形的是( )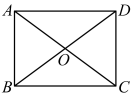 A、 B、 C、 D、4. 如图,在菱形中,对角线 , 相交于点 , 添加下列条件,能使菱形成为正方形的是( )
A、 B、 C、 D、4. 如图,在菱形中,对角线 , 相交于点 , 添加下列条件,能使菱形成为正方形的是( ) A、 B、 C、 D、平分5. 如图,已知四边形的对角线相交于O,则下列条件能判断它是正方形的的是( )
A、 B、 C、 D、平分5. 如图,已知四边形的对角线相交于O,则下列条件能判断它是正方形的的是( ) A、 , B、 C、 , , D、 ,6. 如图,在中,点、、分别在边 , , 上,且 , 下列结论:①四边形是平行四边形;②如果 , 那么四边形是矩形;③如果平分 , 那么四边形是菱形;④如果 , 平分 , 那么四边形是正方形你认为正确的是( )
A、 , B、 C、 , , D、 ,6. 如图,在中,点、、分别在边 , , 上,且 , 下列结论:①四边形是平行四边形;②如果 , 那么四边形是矩形;③如果平分 , 那么四边形是菱形;④如果 , 平分 , 那么四边形是正方形你认为正确的是( ) A、①②③④ B、①②③ C、①②④ D、②③④7. 如图,将一张长方形纸对折,再对折,然后沿图中虚线剪下,剪下的图形展开后可得到( )
A、①②③④ B、①②③ C、①②④ D、②③④7. 如图,将一张长方形纸对折,再对折,然后沿图中虚线剪下,剪下的图形展开后可得到( )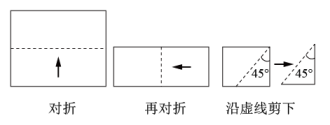 A、三角形 B、梯形 C、正方形 D、五边形8. 一个四边形顺次添加下列中的三个条件便得到正方形:
A、三角形 B、梯形 C、正方形 D、五边形8. 一个四边形顺次添加下列中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等
c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d②b→d→c③a→b→c
则正确的是( )
A、仅① B、仅③ C、①② D、②③二、填空题
-
9. 如图,在矩形 中,对角线 相交于点O,在不添加任何辅助线的情况下,请你添加一个条件 , 使矩形 是正方形.
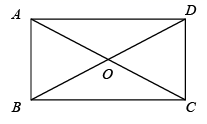 10. 如图,正方形ABCD的边长为3,点E在边AB上,且BE=1,若点P在对角线BD上移动,则PA+PE的最小值是 .
10. 如图,正方形ABCD的边长为3,点E在边AB上,且BE=1,若点P在对角线BD上移动,则PA+PE的最小值是 .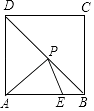 11. 如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:
11. 如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:①四边形是平行四边形;
②当时,四边形是矩形;
③当时,四边形是菱形;
④当 , 且时,四边形是正方形.
其中正确结论有(填上所有正确结论的序号).
 12. 如图,点P是正方形 的对角线 上一点, ,垂足分别为点E , F , 连接 ,给出下列四个结论:① ;② ;③ ;④ 一定是等腰三角形.其中正确的结论序号是 .
12. 如图,点P是正方形 的对角线 上一点, ,垂足分别为点E , F , 连接 ,给出下列四个结论:① ;② ;③ ;④ 一定是等腰三角形.其中正确的结论序号是 . 13. 如图,四边形ABCD中,AD=DC,∠ADC=∠ABC=90°,DE⊥AB,若四边形ABCD面积为16,则DE的长为.
13. 如图,四边形ABCD中,AD=DC,∠ADC=∠ABC=90°,DE⊥AB,若四边形ABCD面积为16,则DE的长为.
三、解答题
-
14. 如图,在矩形中,点E,F分别在边上, , 且 , 与相交于点G.求证:矩形为正方形;
 15. 如图,在菱形中,对角线 , 相交于点 , 点 , 在对角线上,且 , .
15. 如图,在菱形中,对角线 , 相交于点 , 点 , 在对角线上,且 , .求证:四边形是正方形.
 16. 如图,四边形ABCD是矩形,E是BD上的一点,连接AE、CE, , ,求证:四边形ABCD是正方形.
16. 如图,四边形ABCD是矩形,E是BD上的一点,连接AE、CE, , ,求证:四边形ABCD是正方形. 17. 如图,的对角线交于点 , 分别以点为圆心,长为半径画弧,两弧交于点 , 连接 .
17. 如图,的对角线交于点 , 分别以点为圆心,长为半径画弧,两弧交于点 , 连接 . (1)、试判断四边形的形状,并说明理由;(2)、请说明当的对角线满足什么条件时,四边形是正方形?18. 如图,在中, , D、E、F分别是、、的中点.
(1)、试判断四边形的形状,并说明理由;(2)、请说明当的对角线满足什么条件时,四边形是正方形?18. 如图,在中, , D、E、F分别是、、的中点. (1)、求证: .(2)、连接、 , 求证:四边形为矩形.(3)、 满足什么条件时,四边形为正方形,并证明.19. 定义:如果一个凸四边形有三条边相等,那么称这个凸四边形为“准等边四边形”.如正方形就是一个“准等边四边形”.(1)、如图,在给定的网格中,找到格点D.使得以A、B、C、D为顶点的四边形是准等边四边形
(1)、求证: .(2)、连接、 , 求证:四边形为矩形.(3)、 满足什么条件时,四边形为正方形,并证明.19. 定义:如果一个凸四边形有三条边相等,那么称这个凸四边形为“准等边四边形”.如正方形就是一个“准等边四边形”.(1)、如图,在给定的网格中,找到格点D.使得以A、B、C、D为顶点的四边形是准等边四边形 (2)、如图1,▱ABCD中,对角线CA平分∠BCD,将线段CD绕点C顺时针方向旋转一个角度α(0<α<∠B)至CE,连接AE、DE.
(2)、如图1,▱ABCD中,对角线CA平分∠BCD,将线段CD绕点C顺时针方向旋转一个角度α(0<α<∠B)至CE,连接AE、DE.
①求证:四边形ABCE是准等边四边形;
②如图2,连接BE,求证:∠BED=∠ACB;
(3)、如图3,在准等边四边形ABCD中,∠C=90°,AB=BC=CD=2,∠B=150°,请求出∠BAD的大小及该四边形的面积.