河南省漯河市舞阳县2022-2023学年八年级下册数学期末考试试卷
试卷更新日期:2023-07-11 类型:期末考试
一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的,将正确答案的代号字母填入题后括号内.
-
1. 下列函数中,是的正比例函数的是( )A、 B、 C、 D、2. 下面四个点,不在一次函数的图象上的是( )A、 B、 C、 D、3. 下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲
乙
丙
丁
平均数
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表中的数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁4. 一次函数在平面直角坐标系内的图象如图所示,则和的取值范围是( )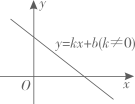 A、 , B、 , C、 , D、 ,5. 在直角坐标系中,已知点 , 点是直线上的两点,则 , 的大小关系是( )A、 B、 C、 D、6. 如图,函数和的图象交于点 , 则不等式的解集为( )
A、 , B、 , C、 , D、 ,5. 在直角坐标系中,已知点 , 点是直线上的两点,则 , 的大小关系是( )A、 B、 C、 D、6. 如图,函数和的图象交于点 , 则不等式的解集为( )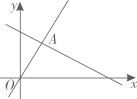 A、 B、 C、 D、7. 为调动学生参与体育锻炼的积极性,某校组织了一分知跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:
A、 B、 C、 D、7. 为调动学生参与体育锻炼的积极性,某校组织了一分知跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:一分钟跳绳个数(个)
141
144
145
146
学生人数(名)
5
2
1
2
则关于这组数据的结论正确的是( )
A、平均数是144 B、众数是141 C、中位数是144.5 D、方差是5.48. 将一圆柱形小水杯固定在大圆柱形容器底面中央,现用一个注水管沿大容器内壁匀速注水,如图所示,则小水杯水面的高度与注水时间的函数图象大致是( )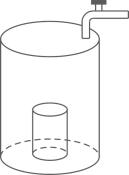 A、
A、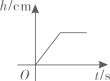 B、
B、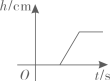 C、
C、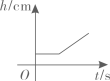 D、
D、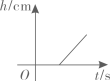 9. 甲、乙两位同学放学后走路回家,他们走过的路程(千米)与所用的时间(分钟)之间的函数关系如图所示.根据图中信息,下列说法错误的是( )
9. 甲、乙两位同学放学后走路回家,他们走过的路程(千米)与所用的时间(分钟)之间的函数关系如图所示.根据图中信息,下列说法错误的是( )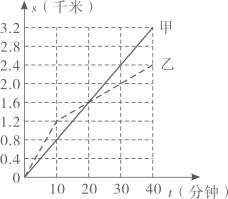 A、前10分钟,甲比乙的速度慢 B、经过20分钟,甲、乙都走了1.6千米 C、甲的平均速度为0.08千米分钟 D、经过30分钟,甲比乙走过的路程少10. 如图,直线分别与轴、轴交于点和点 , 直线分别与轴、轴交于点和点 , 点是内部(包括边上)的一点,则的最大值与最小值之差为( )
A、前10分钟,甲比乙的速度慢 B、经过20分钟,甲、乙都走了1.6千米 C、甲的平均速度为0.08千米分钟 D、经过30分钟,甲比乙走过的路程少10. 如图,直线分别与轴、轴交于点和点 , 直线分别与轴、轴交于点和点 , 点是内部(包括边上)的一点,则的最大值与最小值之差为( ) A、1 B、2 C、4 D、6
A、1 B、2 C、4 D、6二、填空题(每小题3分,共15分)
-
11. 若是二次根式,则的取值范围为。12. 学校举行物理科技创新比赛,各项成绩均按百分制计,然后按照理论知识占 , 创新设计占 , 现场展示占计算选手的综合成绩(百分制),某同学本饮比赛的各项成绩分别是:理论知识85分,创新设计88分,现场展示90分,那么该同学的综合成绩是分.13. 如图,函数的图像经过点 , 则关于的不等式的解集为 .
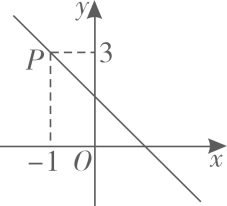 14. 把直线向左平移1个单位长度,再向上平移2个单位长度,则平移后所得直线的解析式为 .15. 如图,在中, . 利用尺规在、上分别截取、 , 使;分别以、为圆心,大于的长为半径作弧,两弧在内交于点;作射线交于点 . 若 , 则的长为 .
14. 把直线向左平移1个单位长度,再向上平移2个单位长度,则平移后所得直线的解析式为 .15. 如图,在中, . 利用尺规在、上分别截取、 , 使;分别以、为圆心,大于的长为半径作弧,两弧在内交于点;作射线交于点 . 若 , 则的长为 .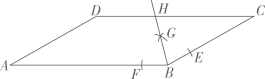
三、解答题(共8小题,满分75分)
-
16. 计算:(1)、;(2)、17. 已知一次函数 , 完成下列问题:
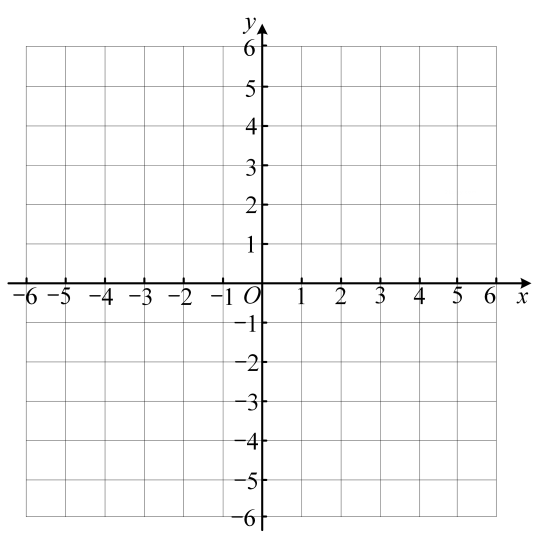 (1)、在所给的平面直角坐标系中画出此函数的图象;(2)、根据函数图象回答:当时, .18. 已知点、分别是平行四边形的边、的中点.
(1)、在所给的平面直角坐标系中画出此函数的图象;(2)、根据函数图象回答:当时, .18. 已知点、分别是平行四边形的边、的中点.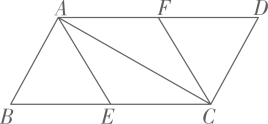 (1)、求证:四边形是平行四边形;(2)、若 , , 求平行四边形的周长.19. 公司生产、两种型号的扫地机器人,为了解它们的扫地质量,工作人员从某月生产的、型扫地机器人中各随机抽取10台,在完全相同条件下试验,记录下它们的除尘量的数据(单位:g),并进行整理、描述和分析(除尘量用表示,共分为三个等级:合格 , 良好 , 优秀),下面给出了部分信息:
(1)、求证:四边形是平行四边形;(2)、若 , , 求平行四边形的周长.19. 公司生产、两种型号的扫地机器人,为了解它们的扫地质量,工作人员从某月生产的、型扫地机器人中各随机抽取10台,在完全相同条件下试验,记录下它们的除尘量的数据(单位:g),并进行整理、描述和分析(除尘量用表示,共分为三个等级:合格 , 良好 , 优秀),下面给出了部分信息:10台型扫地机器人的除尘量:83,84,84,88,89,89,95,95,95,98.
10台型扫地机器人中“良好”等级包含的所有数据为:85,90,90,90,94
抽取的、型扫地机器人除尘量统计表:
型号
中位数
众数
方差
“优秀”等级所占百分比
89
26.6
90
30
根据以上信息,解答下列问题:
(1)、填空: , , .(2)、这个月公司可生产型扫地机器人共3000台,估计该月型扫地机器人“优秀”等级的台数;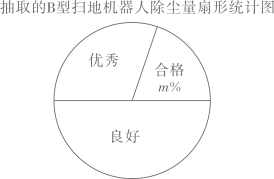 (3)、根据以上数据,你认为该公司生产的哪种型号的扫地机器人扫地质量更好?请说明理由(写出一条理由即可).20. 如图,在平行四边形中,过点作于点 , 点在边上,且 , 连接 , .
(3)、根据以上数据,你认为该公司生产的哪种型号的扫地机器人扫地质量更好?请说明理由(写出一条理由即可).20. 如图,在平行四边形中,过点作于点 , 点在边上,且 , 连接 , .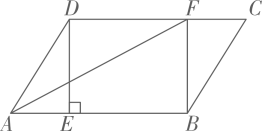 (1)、求证:四边形是矩形;(2)、若平分 , , , 求的长.21. 有一个容量为8GB(1GB=1024MB)的U盘,U盘中已经存储了1个视频文件,其余空间都用来存储照片.若每张照片占用的内存容量均相同,照片数量x(张)和剩余可用空间y(MB)的部分关系如表:
(1)、求证:四边形是矩形;(2)、若平分 , , , 求的长.21. 有一个容量为8GB(1GB=1024MB)的U盘,U盘中已经存储了1个视频文件,其余空间都用来存储照片.若每张照片占用的内存容量均相同,照片数量x(张)和剩余可用空间y(MB)的部分关系如表:照片数量
100
150
200
400
800
剩余可用空间
5600
5400
5200
4400
2800
(1)、求出y与x之间的关系式.(2)、若U盘中已经存入1100张照片,那么最多还能存入多少张照片?22. 在一条平坦笔直的道路上依次有 , , 三地,甲从地骑电瓶车到地,同时乙从地骑摩托车到地,到达地后因故停留1分钟,然后立即掉头(掉头时间忽㕷不计)按原路原速前往地,结果乙比甲早2分钟到达地,两人均匀速运动,如图是两人距地路程(米)与时间(分钟)之间的函数图象.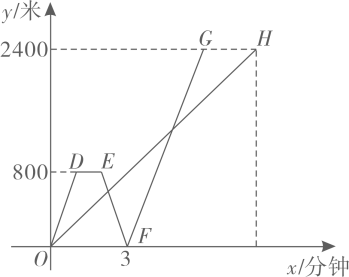
请解答下列问题:
(1)、填空:甲的速度为米/分钟,乙的速度为米/分钟;(2)、求图象中线段所在直线表示的(米)与时间(分钟)之间的函数解析式,并写出自变量的取值范围.23. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、 , 直线与轴交于点 , 与直线交于点 .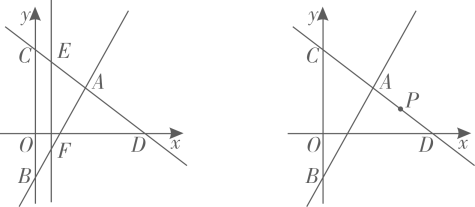 (1)、求直线的解析式;(2)、点是射线上一动点,过点作轴,交直线于点 . 若以O、C、E、F为顶点的四边形是平行四边形,请求出点的坐标;(3)、设是射线上一点,在平面内是否存在点 , 使以B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.
(1)、求直线的解析式;(2)、点是射线上一动点,过点作轴,交直线于点 . 若以O、C、E、F为顶点的四边形是平行四边形,请求出点的坐标;(3)、设是射线上一点,在平面内是否存在点 , 使以B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点的坐标;若不存在,请说明理由.