浙江省宁波市海曙区2022-2023学年七年级下册数学期末考试试卷

试卷更新日期：2023-07-11 类型：期末考试

进入出卷网下载

一、选择题（共10小题，满分30分，每小题3分）

1. 为了解某地一天内的气温变化情况，比较适合使用的统计图是（）

A、条形统计图 B、折线统计图 C、扇形统计图 D、频数分布直方图

查看试题解析
2. 下面各式从左到右的变形，属于因式分解的是（）

A、 $x (x - 1) = x^{2} - x$ B、 $x^{2} - 1 = (x - 1)^{2}$ C、 $x^{2} - x - 1 = x (x - 1) - 1$ D、 $x^{2} - x = x (x - 1)$

查看试题解析
3. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $a^{6} \div a^{2} = a^{3}$ C、 ${(a^{2})}^{3} = a^{6}$ D、 $a^{5} + a^{5} = a^{10}$

查看试题解析
4. 如果把分式 $\frac{x^{2}}{x + y}$ 中 $x ､ y$ 的值都变为原来的2倍，则分式的值（）

A、变为原来的2倍 B、不变 C、变为原来的 $\frac{1}{2}$ D、变为原来的4倍

查看试题解析
5. 如图，点 $E$ 在 $C B$ 的延长线上，下列条件中，能判定 $A D ∥ B C$ 的是（）

A、 $∠ 1 = ∠ 4$ B、 $∠ 2 = ∠ 3$ C、 $∠ A = ∠ C$ D、 $∠ A + ∠ A D C = 18 0^{∘}$

查看试题解析
6. 用代入法解二元一次方程组 ${\begin{array}{l} y = 1 - x ① \\ x + 2 y = 4 ② \end{array}$ 时，将方程①代入方程②，得到结果正确的是（）

A、 $x - 2 - 2 x = 4$ B、 $x + 2 - 2 x = 4$ C、 $x + 2 + x = 4$ D、 $x + 2 - x = 4$

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ A = 6 0^{∘} ， ∠ B = 5 0^{∘}$ ．根据尺规作图痕迹，可得 $∠ A C D$ 的大小为（）

A、 $10 0^{∘}$ B、 $7 0^{∘}$ C、 $2 0^{∘}$ D、 $1 0^{∘}$

查看试题解析
8. 盲盒近来火爆，这种不确定的“盲抽”模式受到了大家的喜爱，一服装厂用某种布料生产玩偶A与玩偶B组合成一批盲盒，一个盲盘搭配1个玩偶A和2个玩偶B，已知每米布料可做1个玩偶A或3个玩偶B，现计划用136米这种布料生产这批盲盘（不考虑布料的损耗），设用x米布料做玩偶A，用y米布料做玩偶B，使得恰好配套，则下列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 136 \\ x = 3 y \end{array}$ B、 ${\begin{array}{l} x + y = 136 \\ 3 x = 2 y \end{array}$ C、 ${\begin{array}{l} x + y = 136 \\ 2 x = 3 y \end{array}$ D、 ${\begin{array}{l} x + y = 136 \\ 3 x = y \end{array}$

查看试题解析
9. 如图，两个正方形的泳池，面积分别是 $S_{1}$ 和 $S_{2}$ ，两个泳池的面积之和 $S_{1} + S_{2} = 16$ ，点 $B$ 是线段 $C G$ 上一点，设 $C G = 6$ ，在阴影部分铺上防滑瓷砖，则所需防滑瓷砖的面积为（）

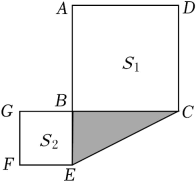A、5 B、4 C、8 D、10

查看试题解析
10. $\frac{2 x - 3}{| x | + 1}$ 为整数，符合条件的整数 $x$ 的个数是（）

A、1 B、2 C、4 D、5

查看试题解析

二、填空题（共6小题，满分18分，每小题3分）

11. 若 $\frac{a}{b} = \frac{1}{2}$ ，则分式 $\frac{3 a + b}{b} =$ ．

查看试题解析
12. 用一根小木棒与两根长分别为 $3 c m ､ 6 c m$ 的小木棒围成三角形，则这根小木棒的长度可以为 $c m ($ 㝍出一个即可）．

查看试题解析
13. 如图，将直角 $△ A B C$ 沿 $C B$ 边向右平移得到 $△ D F E ， D E$ 交 $A B$ 于点 $G . A B = 9 c m ， B F = 3 c m ， A G = 5 c m$ ，则图中阴影部分的面积为 $c m^{2}$ ．

查看试题解析
14. 若 $(x^{2} + m x - 8) (x^{2} - 3 x + n)$ 的展开式中不含 $x^{2}$ 和 $x^{3}$ 项，则 $n$ 的值为．

查看试题解析
15. 若关于 $x ， y$ 的方程组 ${\begin{array}{l} 4 x + y = m + 3 \\ 2 x - y = 2 m \end{array}$ 的解 $x ､ y$ 之和为3，则 $m$ 的值为．

查看试题解析
16. 已知 $a^{2} (b + c) = b^{2} (a + c) = 2023$ ，且 $a ､ b ､ c$ 互不相等，则 $c^{2} (a + b) - 2024 =$ ．

查看试题解析

三、解答题（共8小题，满分52分）

17. 计算：

(1)、 $(- 1)^{3} + (π - 2023)^{0} + {(\frac{1}{2})}^{- 3}$ ；

(2)、 $(x + y) (x - y) + x (y - x) + y^{2}$ ．

查看试题解析
18. 解下列方程（组）

(1)、 ${\begin{array}{l} \frac{x}{2} + \frac{y + 1}{3} = 3 \\ 3 x - 2 (y + 1) = 6 \end{array}$ ；

(2)、 $\frac{2 - x}{x - 3} = \frac{1}{3 - x} - 2$ .

查看试题解析
19. 先化简 $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ，然后从 $- 1 ， 0 ， 1$ 这三个数中选取一个合适的数作为 $x$ 的值代入求值．

查看试题解析

20. 某校为庆祝建党100周年举行“学习党史知识竞赛”活动，全校共有1000名学生参加活动，为了了解本次知识竞赛成绩分布情况，从中随机抽取了部分学生进行统计，请你根据不完整的表格，解答下列问题：

“学习党史知识竞赛”成绩频数表

成绩 $x$ 分	频数	频率
$75 ⩽ x < 80$	10	0.05
$80 ⩽ x < 85$	14	$n$
$85 ⩽ x < 90$	$m$	0.2
$90 ⩽ x < 95$	56	0.28
$95 ⩽ x < 100$	80	0.40

(1)、表中的

m =

，

n =

．

(2)、补全频数分布直方图；

(3)、若规定90分及以上为优秀，则全校有多少学生成绩是优秀的？

查看试题解析

21. 甲、乙两个同学分解因式 $x^{2} + a x + b$ 时，甲看错了 $b$ ，分解结果为 $(x + 2) (x + 4)$ ；乙看错了 $a$ ，分解结果为 $(x + 1) (x + 9)$ ，求 $a + b$ 的值．

查看试题解析
22. 如图1，直线 $C B ∥ O A ， ∠ A = ∠ B = 12 0^{∘} ， E ， F$ 在 $B C$ 上，且满足 $∠ F O C = ∠ A O C$ ，并且 $O E$ 平分 $∠ B O F$ ．

(1)、求 $∠ A O B$ 及 $∠ E O C$ 的度数；

(2)、如图2，若平行移动 $A C$ ，那么 $∠ O C B ： ∠ O F B$ 的值是否随之发生变化？若变化，找出变化规律或求出变化范围；若不变，求出这个比值；

查看试题解析
23. 小能到某体育用品商店购物，他已选定了需购买的篮球和羽毛球拍的种类，若购买3个篮球和8副羽毛球拍共需416元；若购买6个篮球和1副羽毛球拍共需232元．

(1)、求每个篮球和每副羽毛球拍各需多少元？

(2)、“暑假”期间，该体育用品商店举行让利促销活动，篮球和羽毛球拍均以相同折扣进行销售，小能发现用256元购买篮球的个数比用480元购买羽毛球拍的副数少5.
①求商店本次活动对篮球和羽毛球拍进行几折销售？
②小能决定在这次让利促销活动中同时购买篮球和羽毛球拍，最后扫码支付了281.6元，问他有几种购买方案，请说明理由．

查看试题解析
24. 角平分线性质定理描述了角平分线上的点到角两边距离的关系，小储发现将角平分线放在三角形中，有一些新的发现，请完成下列探索过程：

(1)、【知识回顾】
如图1， $P$ 是 $∠ B O A$ 的平分线上的一点， $P E ⊥ O B$ 于点 $E$ ，作 $P D ⊥ O A$ 于点 $D$ ，试证： $P E = P D$

(2)、【深入探究】
如图2，在 $△ A B C$ 中， $B D$ 为 $∠ A B C$ 的角平分线交于 $A C$ 于 $D$ 点，其中 $A B + B C = 10 ， A D = 2 ， C D = 3$ ，求 $A B$ ．

(3)、【应用迁移】
如图3，Rt $△ A B C$ 中， $∠ C = 9 0^{∘} ， ∠ B A C$ 的角平分线 $A E$ 与 $A C$ 的中线 $B D$ 交于点 $F ， P$ 为 $C E$ 中点，连接 $P F$ ，若 $C P = 4 ， S_{△ B F P} = 20$ ，则 $A B$ 的长度为．

查看试题解析