陕西省咸阳市礼泉县2022-2023学年七年级下册数学期末考试试卷

试卷更新日期：2023-07-11 类型：期末考试

进入 出卷网 下载

一、选择题(共8小题，每小题3分，计24分.每小题只有一个选项是符合题意的)

  • 1. 在标准状态下气体分子间的平均距离为0.00033m，将0.00033用科学记数法表示为（ ）
    A、3.3×10-3 B、33×10-3 C、3.3×10-5 D、3.3×10-4

    查看试题解析

  • 2. 下列图形中，不是轴对称图形的是（ ）
    A、 B、 C、 D、

    查看试题解析

  • 3. 下列成语描述的事件是随机事件的是（ ）
    A、日落西山 B、揠苗助长 C、一箭双雕 D、一步登天

    查看试题解析

  • 4. 将一块直角三角板与一把直尺按如图所示方式放置，若∠1=36°，则∠2的度数为（ ）

    A、126° B、144° C、108° D、153°

    查看试题解析

  • 5. 一个小球先沿斜坡向上滚动，再沿斜坡向下滚动，其速度v(单位：m/s)与时间t(单位：s)的图象如图所示.下列说法错误的是（ ）

    A、小球的初始速度为6m/s B、小球在整个滚动过程中，当t=3s时，到达斜坡的最低处 C、当t=3s时，小球的速度v=0m/s D、当t=6s时，小球的速度与初始速度相同

    查看试题解析

  • 6. 如图，点B，E，C，F共线，AB=DE，BE=CF，添加一个条件，不能得到△ABC≌△DEF的是（ ）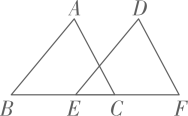

    A、∠B=∠DEF B、AC=DF C、∠A=∠D D、AB∥DE

    查看试题解析

  • 7. 某同学在计算-3x加上一个多项式时错将加法做成了乘法，得到的答案是3x3-3x2+3x，由此可以推断出正确的计算结果是（ ）
    A、-x2-2x-1 B、x2+2x-1 C、-x2+4x-1 D、x2-4x+1

    查看试题解析

  • 8. 如图，在△ABC与△AEF中，AB=AE，BC=EF，∠ABC=∠AEF，∠EAB=40°，AB交EF于点D，连接EB.下列结论：①∠FAC=40°；②AF=AC；③∠EFB=40°；④∠EBC=110°，其中正确的有（ ）

    A、①②③④ B、①②④ C、②③④ D、①②③

    查看试题解析

二、填空题(共5小题，每小题3分，计15分)

  • 9. 如图，请写出一个能使得DE∥BC的条件：.(只写一个即可)

    查看试题解析

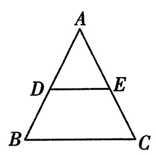  • 10. 设计如图所示的一个转盘(每个扇形的面积相同)，转动一次转盘，当转盘停止转动时，“指针落在白色区域”的概率为.

    查看试题解析

  • 11. 如图，在Rt△ABC中，∠A=90°，BD平分∠ABC交AC于点D，若S△BCD=15，BC=10，.则AD的长为 .

    查看试题解析

  • 12. 一支原长为20cm的蜡烛，点燃后，其剩余长度与燃烧时间的关系如下表：  

    烧烧时间／分

    10

    20

    30

    40

    50

    剩余长度/cm

    19

    18

    17

    16

    15

    当这支蜡烛的剩余长度为10cm时，这支蜡烛燃烧了分钟.

    查看试题解析

  • 13. 如图，在四边形ABEF中，AB=4，EF=6，点C是BE上一点，连接AC、CF，若AC=CF，∠B=∠E=∠ACF，则BE的长为.

    查看试题解析

三、解答题(共13小题，计81分.解答应写出过程)

  • 14. 计算：(−3)2+2×(−14)−1+(−5)0.

    查看试题解析

  • 15. 如图，直线AB与CD相交于点E，∠AEC=60°，∠BEF=95°，求∠CEF的度数.

    查看试题解析

  • 16. 下表记录了一名篮球运动员在罚球线上练习投篮的结果：

    投篮次数(n)

    50

    100

    150

    200

    250

    300

    350

    投中次数(m)

    28

    60

    78

    104

    123

    153

    175

    投中频率(m/n)

    0.56

    0.60

    0.52

    a

    0.49

    0.51

    b

    根据表格中的数据，解答下列问题：

    (1)、求a、b的值；
    (2)、若这名篮球运动员在罚球线上再投篮一次，估计他投中的概率.(结果精确到0.1)

    查看试题解析

  • 17. 如图，直线l是一个轴对称图形的对称轴，在网格中画出这个轴对称图形的另一半.

    查看试题解析

  • 18. 如图，在Rt△ABC中，∠B=90°，CD∥AB，DE⊥AC于点E，且DE=CB.试说明：△CED≌△ABC.

    查看试题解析

  • 19. 如图，已知△ABC，利用尺规作图法在△ABC内求作△BOC，使得.

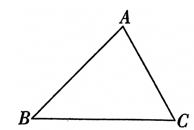
         ∠OBC=12∠ABC ， ∠OCB=12∠ACB.(不写作法，保留作图痕迹)

    查看试题解析

  • 20. 先化简，再求值：[(x+2y)2-(x-2y)(2y+x)]÷4y，其中x=-5，y=2.

    查看试题解析

  • 21. 数学兴趣小组打算测量教室内花瓶的内径，经过搜索资料，发现了一个可以使用的工具—卡钳，它能够解决无法直接测量的问题，可以测量内径长度，于是小组成员决定使用卡钳完成本次任务.利用卡钳测量花瓶内径的示意图如图所示，已知AD=BC，O是线段AD和BC的中点.

    利用卡钳测量内径的步骤为：

    ①将卡钳A，B两端伸入在花瓶内；

    ②打开卡钳，使得A，B两端卡在内壁；

    ③测量出点C与点D间的距离，即为花瓶内径的长度AB.

    请你写出这样测量的理由.

    查看试题解析

  • 22.  2023年5月30日神舟十六号载人飞船成功发射.为了激发青少年了解航天知识的热情，某校组织学生去距离学校1200米的航天博物馆进行参观学习，他们从学校出发步行到博物馆，参观了2小时，然后按照原路线步行返回学校.已知他们离学校的距离y(米)与离开学校的时间t(分)之间的关系如图所示：

    根据图象解答下列问题：

    (1)、在上述问题中，自变量是 ， 因变量是；
    (2)、写出图中点P表示的实际意义；
    (3)、求出图中m的值及从博物馆返回学校的平均速度.

    查看试题解析

  • 23. 如图，在△ABC中，AB=AC，AB的垂直平分线DE分别交AC、AB于点D、E，连接BD.

    (1)、若∠A=50°，求∠CBD的度数；
    (2)、若AB=7，BC的长为5，求△CBD的周长.

    查看试题解析

  • 24. 一个批发商从某服装制造公司购进了50包型号为L的衬衫，由于包装工人的疏忽，在部分包裹中混入了型号为M的衬衫，混入的M号衬衫的件数(件)与对应的包数(包)如下表：

    M号衬衫数(件)

    0

    1

    4

    5

    7

    9

    10

    11

    包数（包）

    7

    3

    10

    15

    5

    4

    3

    3

    一位零售商从50包中任意选取了一包，求下列事件的概率：

    (1)、包中没有混入M号的衬衫；
    (2)、包中有混入M号的衬衫且件数小于7件；
    (3)、包中混入M号衬衫的件数大于9件.

    查看试题解析

  • 25. 如图，在△ABC中，∠B=42°，∠C=68°，点E为线段AB的中点，点F在边AC上，连接EF，沿EF将△AEF折叠得到△PEF.

    (1)、如图1，当点P落在BC上时，求∠BEP的度数；
    (2)、如图2，当PF⊥AC时，求∠AEF的度数.

    查看试题解析

  • 26. 【问题背景】

    如图，已知△AOB≌△COD，OD与AB交于点G，OB与CD交于点E.

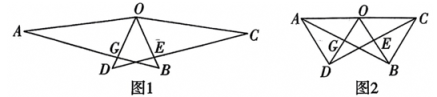    (1)、【问题提出】

    如图1，∠AOD与∠COB的数量关系是：∠AOD∠COB；(填“>”“<”或“=”)

    (2)、【问题探究】

    如图1，判断BG和DE是否相等，并说明理由；

    (3)、如图2，若OA=OB，当A，O，C三点共线，且OB⊥CD时，求∠AOD的度数.

    查看试题解析