陕西榆林市省定边县2022-2023学年八年级下册数学期末考试试卷
试卷更新日期:2023-07-11 类型:期末考试
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
-
1. 下列分式中,最简分式是( )A、 B、 C、 D、2. 下列图标中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,OD平分 , 于点E, , F是射线OB上的任意一点,则DF的长度不可能是( )
3. 如图,OD平分 , 于点E, , F是射线OB上的任意一点,则DF的长度不可能是( )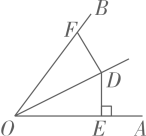 A、4 B、5 C、5.5 D、64. 若多项式可分解为 , 则的值为( )A、-11 B、11 C、-3 D、35. 如图,将绕点A逆时针旋转60°得到 , 若 , 且于点F,则的度数为( )
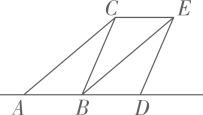
A、4 B、5 C、5.5 D、64. 若多项式可分解为 , 则的值为( )A、-11 B、11 C、-3 D、35. 如图,将绕点A逆时针旋转60°得到 , 若 , 且于点F,则的度数为( ) A、70° B、75° C、80° D、85°6. 如图,爷爷家有一块等边三角形的空地ABC,已知点E,F分别是边AB,AC的中点,量得米,爷爷想把四边形BCFE用篱笆围成一圈种植蔬菜,则需要篱笆的长是( )
A、70° B、75° C、80° D、85°6. 如图,爷爷家有一块等边三角形的空地ABC,已知点E,F分别是边AB,AC的中点,量得米,爷爷想把四边形BCFE用篱笆围成一圈种植蔬菜,则需要篱笆的长是( ) A、16米 B、22米 C、27米 D、30米7. 若关于的不等式组恰有两个整数解,则的取值范围是( )A、 B、 C、 D、8. 在平面直角坐标系中的位置如图所示, , , 则点B的坐标为( )
A、16米 B、22米 C、27米 D、30米7. 若关于的不等式组恰有两个整数解,则的取值范围是( )A、 B、 C、 D、8. 在平面直角坐标系中的位置如图所示, , , 则点B的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共5小题,每小题3分,计15分)
-
9. 已知 , 则.(填“>”或“<”)10. 如果一个多边形的内角和是外角和的2倍,则这个多边形是边形.11. 如图,将沿直线AB向右平移得到 , 连接CE,若的周长为9,四边形ADEC的周长为15,则平移的距离为.
 12. 若关于x的分式方程的解为 , 则.13. 在中, , , , 以的边AC为一边作等腰 , 它的一个顶点D在的边AB上,那么这个等腰三角形的腰长为.
12. 若关于x的分式方程的解为 , 则.13. 在中, , , , 以的边AC为一边作等腰 , 它的一个顶点D在的边AB上,那么这个等腰三角形的腰长为.三、解答题(共13小题,计81分,解答应写出过程)
-
14. 因式分解:.15. 解不等式 , 并将解集在数轴上表示出来.
 16. 先化简,再求值: , 其中.17. 解分式方程: .18. 在网格图中的位置如图所示,三个顶点都在格点上.
16. 先化简,再求值: , 其中.17. 解分式方程: .18. 在网格图中的位置如图所示,三个顶点都在格点上.
⑴画出将向右平移6个单位长度得到的;
⑵画出关于原点O的中心对称图形;
⑶画出绕原点O逆时针旋转90°后得到的.
19. 如图,在四边形ABCD中, , 连接AC,且 , 点E在边BC上,连接DE,过点A作 , 垂足为F,.求证:.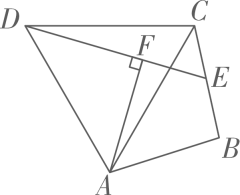 20. 中国是最早发现和利用茶树的国家,被称为茶的祖国.某茶店用9600元购进A种茶叶若干盒,用6720元购进B种茶叶若干盒,所购A种茶叶比B种茶叶多10盒.已知B种茶叶每盒进价是A种茶叶每盒进价的1.2倍.分别求出A,B两种茶叶的每盒进价.(列分式方程解)21. 19世纪的法国数学家苏菲·热门给出了一种分解因式的方法:他抓住了该式只有两项,而且属于平方和的形式,要使用公式就必须添一项 , 随即将此项减去,即可得.人们为了纪念苏菲·热门给出这一解法,就把它叫做“热门定理”。
20. 中国是最早发现和利用茶树的国家,被称为茶的祖国.某茶店用9600元购进A种茶叶若干盒,用6720元购进B种茶叶若干盒,所购A种茶叶比B种茶叶多10盒.已知B种茶叶每盒进价是A种茶叶每盒进价的1.2倍.分别求出A,B两种茶叶的每盒进价.(列分式方程解)21. 19世纪的法国数学家苏菲·热门给出了一种分解因式的方法:他抓住了该式只有两项,而且属于平方和的形式,要使用公式就必须添一项 , 随即将此项减去,即可得.人们为了纪念苏菲·热门给出这一解法,就把它叫做“热门定理”。根据以上方法,把下列各式因式分解:
(1)、;(2)、.22. 某村在政府的扶持下建起了鲜花大棚基地,准备种植百合、玫瑰这两种鲜花.经测算,种植这两种鲜花每亩的投入与获利情况如表:每亩需投入(万元)
每亩可获利(万元)
玫瑰
4
1.2
百合
2
0.8
设种植百合x亩,总获利y万元.
(1)、若投入200万元全部用来种植这两种鲜花,求y关于x的函数表达式;(2)、在(1)的条件下,若要求种植百合的面积不能多于种植玫瑰的面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.23. 如图,在中, , EF垂直平分AC,交AC于点F,交BC于点E,点D是BE的中点. (1)、若 , 求的度数;(2)、若 , , 求的周长.
(1)、若 , 求的度数;(2)、若 , , 求的周长.


