陕西省咸阳市礼泉县2022-2023学年八年级下册数学期末考试试卷
试卷更新日期：2023-07-11 类型：期末考试
一、选择题(共8小题，每小题3分，计24分.每小题只有一个选项是符合题意的)
-
1. 下列既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
2. 若m>-1，则下列各式中正确的是（ ）A、4m>-4 B、5m<-5 C、m+1<0 D、-m>13. 如图，在▱ABCD中，若∠A=100°，AB=2，则下列结论正确的是（ ）
A、∠B=100° B、∠D=100° C、CD=2 D、AD=24. 如图，△ADE是由△ABC绕A点旋转得到的，若∠C=50°，∠B=90°，∠CAD=10°，则旋转角的度数为（ ）
A、10° B、30° C、40° D、50°5. 某地需要开辟一条隧道，隧道AB的长度无法直接测量.如图所示，在地面上取一点C，使C到A、B两点均可直接到达，测量找到AC和BC的中点D、E，测得DE的长为1100m，则隧道AB的长度为（ ）
A、3300m B、2200m C、1100m D、550m6. 若关于x的分式方程有增根，则a的值是（ ）A、－2 B、－1 C、0 D、17. 如图，在△ABC中，∠C=90°，AC=1，∠B=30°，D是BC上一点，连接AD，设△ADB和△ADC的面积分别是S1 ， S2 ， 且S1：S2=2：1，则∠DAC的度数是（ ）
A、15° B、25° C、30° D、45°8. 如图，点O是▱ABCD对角线的交点，EF过点O分别交AD，BC于点E，F.下列结论：①OE=OF；②AB=BF；③∠DOC=∠OCD；④∠CFE=∠DEF，其中正确结论的个数是（ ）
A、1个 B、2个 C、3个 D、4个二、填空题(共5小题，每小题3分，计15分)
-
9. 若分式的值等于0，则x的值是.10. 分解因式：2x-x²=.11. 如图，直线y₁=x+b与y₂=kx-1相交于点P，点P的横坐标为-1，则关于x的不等式x+b>kx-1的解集是.
12. 如图，在正五边形ABCDE中，以AB为一边，在正五边形内作正方形ABMN，则∠CBM=°.
13. 如图，▱ABCD的顶点C在等边△BEF的边BF上，点E在AB的延长线上，连接DE，G为DE的中点，连接CG.若AD=5，AB=CF=3，则CG的长为.
三、解答题(共13小题，计81分.解答应写出过程)
-
14. 因式分解：x4-81.15. 解分式方程： .16. 如图，在△ABC中，∠ACB为钝角，请用尺规作图法在AB上找一点D，连接CD，使得CD=BD.(不写作法，保留作图痕迹)
17. 如图，在四边形ABCD中，AB=CD，AD=BC，延长CD至点E，连接AE，使得2∠E=∠B，求证：△ADE是等腰三角形.
18. 如图所示，延长△ABC的中线BD至点E，使DE=BD，连接AE、CE.求证：四边形ABCE是平行四边形.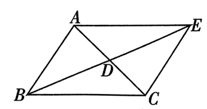
19. 解不等式组：并把它的解集表示在数轴上.
20. 先化简，再求值：其中x=10.21. 利用因式分解计算：(1)、(2)、已知：x+y=1，求的值.22. 如图，在▱ABCD中，E，F分别是AD，BC边上的点，且DE=CF，BE和AF的交点为M，CE和DF的交点为N，连接MN，EF.
(1)、求证：四边形ABFE为平行四边形；(2)、若AD=6cm，求MN的长.23. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(1，3)，B(4，2)，C(2，1).
⑴平移△ABC，使得点A的对应点A₁的坐标为(-1，-1)，画出平移后的△A₁B₁C₁，并写出点C的对应点C₁的坐标；
⑵将△ABC绕原点O逆时针旋转180°得到△A₂B₂C₂，在图中画出△A₂B₂C₂.
24. 如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，EB平分∠DEC.
(1)、求证：BC=CE；(2)、若CE=AB，EA=EB，求∠C的度数.25. 为鼓励物理兴趣小组开展实验项目，某学校决定购入A，B两款物理实验套盒，其中A款套盒单价是B款套盒单价的1.2倍，用9900元购买的A款套盒数量比用7500元购买的B款套盒数量多5个.(1)、求A，B两款物理实验套盒的单价分别是多少元/个?(2)、若学校准备用不超过3400元的金额购买A，B两款物理实验套盒共20个，则至少要购买B款物理实验套盒多少个?26. 如图1，在△OAB中，∠OAB=90°，∠AOB=30°，OB=8.以OB为边，在△OAB外作等边△OBC，D是OB的中点，连接AD并延长交OC于E.
(1)、求证：△ABD≌△EOD；(2)、求证：四边形ABCE是平行四边形；(3)、如图2，将图1中的四边形ABCO折叠，使点C与点A重合，折痕为FG，求OG的长.