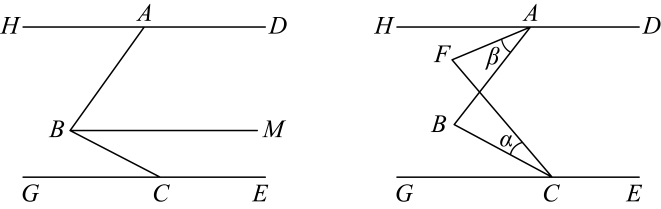陕西省咸阳市武功县2022-2023学年七年级下册数学期中质量调研试卷

试卷更新日期：2023-07-11 类型：期中考试

进入出卷网下载

一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是符合题意的）

1. 可燃冰是一种新型能源，它的密度很小， $1 c m^{3}$ 可燃冰的质量仅为 $0.00092 k g$ ．数据 $0.00092$ 用科学记数法表示为（）

A、 $92 \times 1 0^{- 3}$ B、 $9.2 \times 1 0^{- 4}$ C、 $92 \times 1 0^{- 5}$ D、 $0.92 \times 1 0^{- 3}$

查看试题解析
2. 如图， $∠ 2$ 和 $∠ 4$ 的位置关系是（）

A、内错角 B、同位角 C、同旁内角 D、对顶角

查看试题解析
3. 如图，有三个快递员都从位于点P的快递站取到快递后，同时以相同的速度把取到的快递分别送到位于笔直公路l旁的三个快递点A、B、C、结果送到B快递点的快递员先到．理由是（）

A、垂线段最短 B、两点之间线段最短 C、两点确定一条直线 D、经过一点有无数条直线

查看试题解析
4. 某海滨浴场某日气温变化情况如图所示，该浴场气温在 $32 ℃$ 以上时才允许游泳，请根据图象分析该浴场在这一天开放的时间为（）

A、5小时 B、8小时 C、12小时 D、10小时

查看试题解析
5. 计算 ${(- 2 x^{4} y)}^{3}$ 的结果是（）

A、 $- 2 x^{4} y^{3}$ B、 $- 8 x^{4} y^{3}$ C、 $- 8 x^{12} y^{3}$ D、 $- 2 x^{12} y^{3}$

查看试题解析
6. 如图，下列条件中，能判定 $A B ∥ C D$ 的是（）

A、 $∠ 1 = ∠ 4$ B、 $∠ 4 = ∠ 6$ C、 $∠ 2 + ∠ 5 = 180 °$ D、 $∠ 1 + ∠ 3 = 180 °$

查看试题解析
7. 已知-4a与一个多项式的积是 $16 a^{3} + 12 a^{2} + 4 a$ ，则这个多项式是（）

A、 $- 4 a^{2} + 3 a$ B、 $4 a^{2} - 3 a$ C、 $4 a^{2} - 3 a + 1$ D、 $- 4 a^{2} - 3 a - 1$

查看试题解析

8. 某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据：

温度（ $° C$ ）	$- 20$	$- 10$	$0$	$10$	$20$	$30$
声速（ $m / s$ ）	$318$	$324$	$330$	$336$	$342$	$348$

下列说法中错误的是（）

A、在这个变化中，温度是自变量，声速是因变量 B、空气温度每升高

10 ° C

，声速就增加

6 m / s

C、由表中数据可推测，在一定范围内，空气温度越高，声速越快 D、当空气温度为

20 ° C

时，声音

5 s

可以传播

1740 m

查看试题解析

二、填空题（共5小题，每小题3分，计15分）

9. 若x+y＝2，则3^x•3^y的值为．

查看试题解析
10. 如图，三角形 $A B C$ 中， $A C ⊥ B C$ ， $C D ⊥ A B$ ，则点 $A$ 到直线 $B C$ 的距离是线段的长度．

查看试题解析
11. 某工厂剩余煤量 $y$ 吨与烧煤天数 $x$ 天满足函数关系 $y = 90 - 6 x$ ，则工厂每天烧煤量是吨．

查看试题解析
12. 对任意整数n，按照下面的运算程序计算，输出的结果为．

查看试题解析
13. 如图，点C在线段 $B F$ 上， $∠ A C D = ∠ D A C ， ∠ A C D + ∠ A C F = 180 °$ ，点E在 $A C$ 上，若 $∠ C B E = ∠ D$ ， $∠ D C F = 5 0^{o}$ ，则 $∠ B E C$ 的度数为 $°$ ．

查看试题解析

三、解答题（共13小题，计81分．解答应写出过程）

14. 计算： $- (- 5) + {(- 3.14)}^{0} - 27 \times {(- 3)}^{- 2}$ ．

查看试题解析
15. 已知 ${(a^{m})}^{n} = a^{2}$ ， ${(a^{m})}^{2} \div a^{n} = a^{3}$ ，求 $m n + 2 m - n$ 的值．

查看试题解析
16. 一个角的补角比这个角的 $4$ 倍大 $15 °$ ，求这个角的度数．

查看试题解析
17. 如图，在三角形 $A B C$ 中， $B D$ 交 $A C$ 于点D，利用尺规作图法在 $A B$ 上求作点E，使得 $∠ A E D = ∠ A B C$ ．（不写作法，保留作图痕迹）

查看试题解析
18. 如图， $P N$ 交 $M Q$ 于点B，已知 $A B ∥ M N$ ， $∠ P = ∠ N$ ．试说明： $∠ Q = ∠ A B M$ ．

查看试题解析
19. 如图，反映了小明从家出发到超市购物以及从超市返回家的过程中，小明离家的距离与时间之间的关系：

(1)、小明在超市购物用了分钟；

(2)、小明往返途中一共用了多长时间？

(3)、小明从家到超市的平均速度是多少？

查看试题解析
20. 先化简，再求值： $[{(a - 2 b)}^{2} - (a - 2 b) (a + 2 b)] \div 2 b$ ，其中 $a = 1$ ， $b = - 2$ ．

查看试题解析
21. 学习了《整式的乘除》这一章之后，小明联想到小学除法运算时，会碰到余数的问题，那么类比多项式除法也会出现余式的问题．例如，如果一个多项式（设该多项式为A）除以 $2 x^{2}$ 的商为 $3 x + 4$ ，余式为 $x - 1$ ，那么这个多项式是多少？他通过类比小学除法的运算法则：被除数＝除数×商＋余数，推理出多项式除法法则：被除式＝除式×商＋余式．
请根据以上材料，解决下列问题：

(1)、请你帮小明求出多项式A；

(2)、小明继续探索，如果一个多项式除以3x的商为 $2 x^{2} + x - 1$ ，余式为 $x + 3$ ，请你根据以上法则求出该多项式．

查看试题解析

22. 在日常生活中，我们经常要烧开水，下表是对烧水的时间与水的温度的记录：

时间（分）	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$	$10$	$11$	$12$	$13$
温度（ $℃$ ）	$25$	$29$	$32$	$43$	$52$	$61$	$72$	$81$	$90$	$98$	$100$	$100$	$100$

根据表格中的数据解答下列问题：

(1)、第5分钟，水的温度是

℃

，从第分钟开始，水的温度升高到

100 ℃

；

(2)、从第

4

分钟到第

9

分钟，水的温度升高了多少？

(3)、继续加热，请你估计在第

15

分钟时，水的温度是多少？随着加热时间的增加，水的温度是否会一直上升？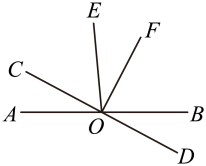

查看试题解析

23. 如图，直线 $A B ， C D$ 交于点O，已知 $O F ⊥ C D$ ， $∠ C O E = 2 ∠ A O C$ ．

(1)、若 $∠ B O D = 28 °$ ，求 $∠ C O E$ 的度数；

(2)、若 $∠ B O F = 60 °$ ，判断 $O E$ 与 $A B$ 的位置关系，并说明理由．

查看试题解析
24. 李叔叔要用篱笆围成一个长方形的果园，已知长方形的宽为 $x$ 米，长比宽长 $10$ 米．当长方形的宽由小到大变化时，长方形的面积也随之发生变化．

(1)、求长方形果园的面积 $y$ （平方米）与 $x$ 之间的关系式；

(2)、当长方形果园的宽为 $30$ 米时，求长方形果园的面积；

(3)、当长方形果园的长恰好是宽的 $2$ 倍时，求长方形果园的面积．

查看试题解析
25. 甲、乙两个长方形的边长如图所示，其面积分别记为 $S_{1}$ ， $S_{2}$ ．

(1)、请通过计算比较 $S_{1}$ 与 $S_{2}$ 的大小；

(2)、若一个正方形的周长等于甲、乙两个长方形的周长的和，设该正方形的面积为 $S_{3}$ ，试说明代数式 $S_{3} - 2 (S_{1} + S_{2})$ 的值是一个常数．

查看试题解析
26. 【问题背景】
如图，点A是直线 $H D$ 上一点，点C是直线 $G E$ 上一点，B是直线 $H D 、 G E$ 之间的一点，连接 $A B ， B C$ ， $D H ∥ G E$ ．

(1)、如图1，过点B作 $B M ∥ D H$ ，试说明： $∠ H A B + ∠ B C G = ∠ A B C$ ；

(2)、如图2，作 $∠ B C F = ∠ B C G$ ， $C F$ 与 $∠ B A H$ 的角平分线交于点F，若 $α + β = 50 °$ ，求 $∠ B + ∠ F$ 的度数

查看试题解析