（人教版）2023-2024学年八年级数学上册11.2与三角形有关的角 同步分层训练（培优卷）
试卷更新日期：2023-07-11 类型：同步测试
一、选择题
-
1. 如图△ABC中，∠A=96°，延长BC到D，∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2 ， 依此类推，∠A4BC与∠A4CD的平分线相交于点A5 ， 则∠A5的度数为（ ）
A、19.2° B、8° C、6° D、3°2. 如图，已知的内角 ， 分别作内角与外角的平分线，两条平分线交于点 ， 得；和的平分线交于点 ， 得；……以此类推得到 ， 则的度数是（ ）
A、 B、 C、 D、3. 如图，在△ABC中，∠BAC＝90°，AD是高，BE是中线，CF是角平分线，CF交AD于点G ， 交BE于点H ， 以下结论：①S△ABE＝S△BCE；②∠AFG＝∠AGF；③∠FAG＝2∠ACF；④AF＝FB ． 其中正确结论的个数有（ ）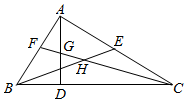
A、4个 B、3个 C、2个 D、1个4. 如图，在△ABC中，∠BAC＝90°，AD是高，BE是中线，CF是平分线，CF交AD于点G，交BE于点H，下列结论①S△ABE＝S△BCE；②∠AFG＝∠AGF；③BH＝CH；④∠FAG＝2∠ACF.正确的是（ ）
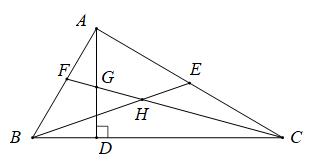A、①②③ B、③④ C、①②④ D、①②③④5. 如图，BF是∠ABD的平分线，CE是∠ACD的平分线，BF与CE交于G ， 若∠BDC＝130°，∠BGC＝100°，则∠A的度数为（ ）
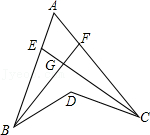A、60° B、70° C、80° D、90°6. 如图，在△ABC中，∠BAC＝90°，AD是高，BE是中线，CF是角平分线，CF交AD于点G，交BE于点H，下面说法：①△ABE的面积＝△BCE的面积；②∠AFG＝∠AGF；③∠FAG＝2∠ACF；④BH＝CH．其中正确的是（ ）
A、①②③④ B、①②③ C、②④ D、①③7. 如图，在△ABC中，BE平分∠ABC交AC于点E ， CD⊥AC交AB于点D ， ∠BCD=∠A ， 则∠BEA的度数（ ）
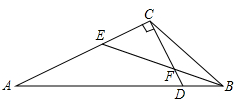A、155° B、135° C、108° D、100°8. 如图，在中， ， 是的高线，是的角平分线，则的度数是（ ）
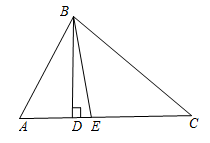A、 B、 C、 D、9. 如图，在中， ， 的度数为α．点P在边上（点P不与点B，点C重合），作于点D，连接 ， 取上一点E，使得 ， 连接 ， 并延长交于点F之后，有 ． 若记的度数为x，则下列关于的表达式正确的是（ ）
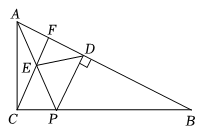A、 B、 C、 D、10. 如图，在中，、的平分线 ， 相交于点F， ， 则（ ）
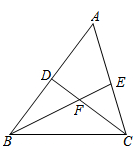A、 B、 C、 D、二、填空题
-
11. 已知一个包装盒的底面是内角和为720°的多边形，它是由另一个多边形纸片剪掉一个角以后得到的，则原多边形是边形．12. 如图，在△ABC 中，∠ABC=57°， ∠BAD=71° ，∠DAC=30° ，∠ACD=11° ，求∠DBC 的度数.
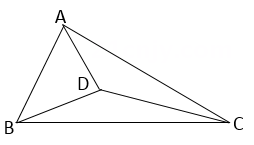13. 如图4，在△ABC中，两条角平分线BD和CE相交于点O，若∠BOC=116°，那么∠A的度数是。
14. 如图，∠ACD是△ABC的一个外角，∠ABC的平分线与∠ACD的平分线交于点 ， 的角平分线与 的平分线交于点 ，若∠A＝60°，则 的度数为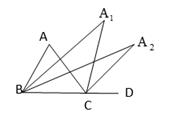
15. 如图，∠ABC＝∠ACB ， BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC ， 以下结论：①AD∥BC；②DB⊥BE；③∠BDC+∠ABC＝90°；④∠A+2∠BEC＝180°．其中正确的结论有 ． （填序号）
三、解答题
-
16. 学习了平行线的判定与性质后，某兴趣小组提出如下问题：
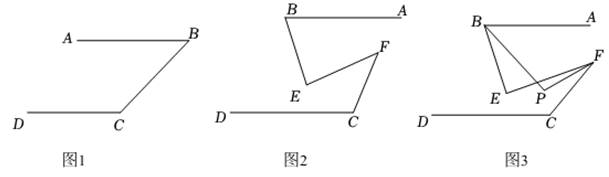
已知：如图， ．
【初步感知】如图1，若 ， 求的度数；
【拓展延伸】如图2，当点、在两平行线之间，且在位于异侧时，求证：；
【类比探究】如图3，若 ， ， 若 ， ， 直接写出的度数．
17. 如图1，AB与CD相交于点O，若∠D=38°，∠B=28°，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试求：
(1)、∠P的度数；(2)、设∠D=α，∠B=β，∠DAP= ∠DAB，∠DCP= ∠DCB，其他条件不变，如图2，试问∠P与∠D、∠B之间存在着怎样的数量关系（用α、β表示∠P），直接写出结论．18. 小明在学习过程中，对教材中的一个有趣问题做如下探究：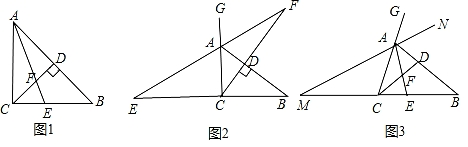
【习题回顾】已知：如图1，在△ABC中，∠ACB＝90°，AE是角平分线，CD是高，AE、CD相交于点F．求证：∠CFE＝∠CEF；
【变式思考】如图2，在△ABC中，∠ACB＝90°，CD是AB边上的高，若△ABC的外角∠BAG的平分线交CD的延长线于点F，其反向延长线与BC边的延长线交于点E，则∠CFE与∠CEF还相等吗？说明理由；
【探究延伸】如图3，在△ABC中，在AB上存在一点D，使得∠ACD＝∠B，角平分线AE交CD于点F．△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M．试判断∠M与∠CFE的数量关系，并说明理由．
19. 如图，已知平面内有两条直线AB、CD，且AB∥CD，P为一动点．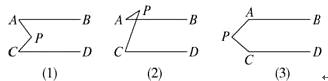
(1)、当点P移动到AB、CD之间时，如图（1），这时∠P与∠A、∠C有怎样的关系？证明你的结论．(2)、当点P移动到AB的外侧时，如图（2），是否仍有（1）的结论？如果不是，请写出你的猜想（不要求证明）．
(3)、当点P移动到如图（3）的位置时，∠P与∠A、∠C又有怎样的关系？能否利用（1）的结论来证明？还有其他的方法吗？请写出一种．四、综合题
-
20. 问题情景：如图1，在同一平面内，点B和点C分别位于一块直角三角板的两条直角边上，点A与点P在直线的同侧，若点P在内部，试问 ， 与的大小是否满足某种确定的数量关系？
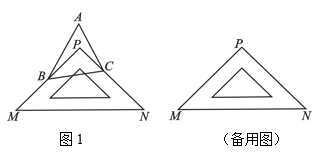(1)、特殊探究：若 ， 则度，度，度；(2)、类比探索：请猜想与的关系，并说明理由；(3)、类比延伸：改变点A的位置，使点P在外，其它条件都不变，判断（2）中的结论是否仍然成立？若成立，请说明理由；若不成立，请直接写出 ， 与满足的数量关系式．21. 如图，在△ABC中，AE，CD分别是∠BAC， ∠ACB的平分线，且AE，CD相交于点F.
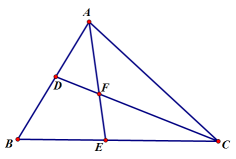(1)、若∠BAC=80°，∠ACB=40°，求∠AFC的度数；(2)、若∠B=80°，求∠AFC的度数；(3)、若∠B=x°，用含x的代数式表示∠AFC的度数.22. 如图1，AB∥CD，点E，分别在直线 ， AB上，∠BEC＝2∠BEF，过点作的延长线于点 ， 交CD于点N，AK平分∠BAG，交于点 ， 交BE于点M.
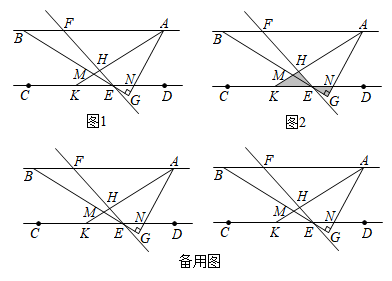(1)、直接写出∠AHE，∠FAH，∠KEH之间的关系：＝+；(2)、若∠BEF＝∠BAK，求∠AHE；(3)、如图2，在（2）的条件下，将△KHE绕着点E以每秒5°的速度逆时针旋转，旋转时间为 ， 当边与射线ED重合时停止，则在旋转过程中，当的其中一边与的某一边平行时，直接写出此时t的值.23.
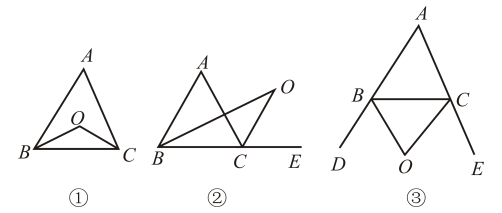(1)、如图①，在中，的平分线与的平分线交于点O，求证：(2)、如图②，在中， E是边BC延长线上一点，的平分线与的平分线交于点O，求证：；(3)、如图③，在中，D是边延长线上一点，E是边延长线上一点，的平分线与的平分线交于点O.①试探求∠A与的数量关系并证明你的结论；
②按角的大小来判断的形状.