(人教版)2023-2024学年八年级数学上册11.2与三角形有关的角 同步分层训练(提升卷)
试卷更新日期:2023-07-11 类型:同步测试
一、选择题
-
1. 若三角形三个内角度数比为 , 则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定2. 若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )A、60° B、50° C、40° D、30°3. 如图,在中, , 是的高线,是的角平分线,则的度数是( )
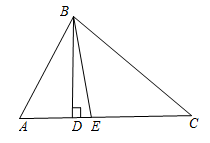 A、 B、 C、 D、4. 如图,在中, , 的度数为α.点P在边上(点P不与点B,点C重合),作于点D,连接 , 取上一点E,使得 , 连接 , 并延长交于点F之后,有 . 若记的度数为x,则下列关于的表达式正确的是( )
A、 B、 C、 D、4. 如图,在中, , 的度数为α.点P在边上(点P不与点B,点C重合),作于点D,连接 , 取上一点E,使得 , 连接 , 并延长交于点F之后,有 . 若记的度数为x,则下列关于的表达式正确的是( )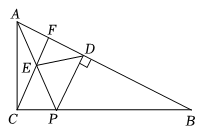 A、 B、 C、 D、5. 如图,在中, , 中线与角平分线相交于点 , 已知 , 则的度数为( )
A、 B、 C、 D、5. 如图,在中, , 中线与角平分线相交于点 , 已知 , 则的度数为( )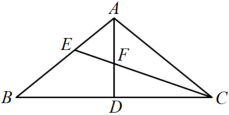 A、 B、 C、 D、6. 将一副直角三角板如图放置,使两直角边重合,则的度数为( )
A、 B、 C、 D、6. 将一副直角三角板如图放置,使两直角边重合,则的度数为( ) A、 B、 C、 D、7. 如图,在中,点D在边上, , , 则等于( )
A、 B、 C、 D、7. 如图,在中,点D在边上, , , 则等于( ) A、80° B、70° C、60° D、50°8. 如图,是的一个外角,E是边AB上一点,下列结论错误的是( )
A、80° B、70° C、60° D、50°8. 如图,是的一个外角,E是边AB上一点,下列结论错误的是( ) A、 B、 C、 D、9. 如图,是的外角的平分线,若 , , 则( )
A、 B、 C、 D、9. 如图,是的外角的平分线,若 , , 则( ) A、35° B、40° C、45° D、55°10. 如图,将一副三角板按如图所示的方式放置,图中等于( )
A、35° B、40° C、45° D、55°10. 如图,将一副三角板按如图所示的方式放置,图中等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,直线 , 且于点C,若 , 则的度数为.
 12. 已知△ABC中,∠A=∠B=∠C,则△ABC是 三角形.13. 如图,在中,平分 , 于点E, , , 则°.
12. 已知△ABC中,∠A=∠B=∠C,则△ABC是 三角形.13. 如图,在中,平分 , 于点E, , , 则°. 14. 如图,在中,延长至D,延长至E,如果 , 则 .
14. 如图,在中,延长至D,延长至E,如果 , 则 . 15. 如图,直线 , 则的度数是 .
15. 如图,直线 , 则的度数是 .
三、解答题
-
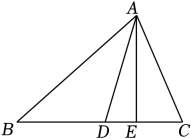
16. 如图:已知在△ABC中,AD平分∠BAC,AE⊥BC,垂足为E,∠B=38°,∠C=70°,求∠DAE的度数.
 17. 如图,在中,延长至点 , 连接 , 是上一点.已知 , , , 求的度数.
17. 如图,在中,延长至点 , 连接 , 是上一点.已知 , , , 求的度数. 18. 如图,在中, , , 的外角的平分线交的延长线于点E.求的度数.
18. 如图,在中, , , 的外角的平分线交的延长线于点E.求的度数.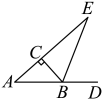 19. 如图,在中,平分 , , .求 , 的度数.
19. 如图,在中,平分 , , .求 , 的度数.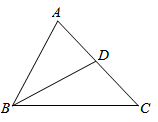
四、综合题
-
20. 如图,AE平分∠BAC,∠CAE=∠CEA.
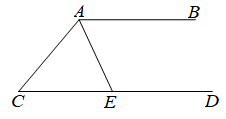 (1)、AB与CD有怎样的位置关系?为什么?(2)、若∠C=50°,求∠CEA的度数.21. 如图1, , 是直线上两点,点在点左侧,过点的直线与过点的直线交于点.直线交直线于点 , 满足点在线段上,.
(1)、AB与CD有怎样的位置关系?为什么?(2)、若∠C=50°,求∠CEA的度数.21. 如图1, , 是直线上两点,点在点左侧,过点的直线与过点的直线交于点.直线交直线于点 , 满足点在线段上,. (1)、求证:;(2)、如图2,点在直线 , 之间,平分 , 平分 , 点 , , 在同一直线上,且 , 求的度数;(3)、在(2)的条件下,若点是直线上一点,直线交直线于点 , 点在点左侧,请直接写出和的数量关系.(题中所有角都是大于且小于的角)
(1)、求证:;(2)、如图2,点在直线 , 之间,平分 , 平分 , 点 , , 在同一直线上,且 , 求的度数;(3)、在(2)的条件下,若点是直线上一点,直线交直线于点 , 点在点左侧,请直接写出和的数量关系.(题中所有角都是大于且小于的角)

