黑龙江省佳木斯市富锦重点中学2023年数学中考二模试卷
试卷更新日期:2023-07-11 类型:中考模拟
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列运算中,计算正确的是( )A、 B、 C、 D、2. 下列图象中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方形的个数最少有 个.( )
3. 如图是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方形的个数最少有 个.( ) A、 B、 C、 D、4. 若一组数据 , , , , 的平均数为 , 则这组数据的中位数和众数分别是( )A、 , B、 , C、 , D、 ,5. 某校“研学”活动小组在一次野外实践时,发现一种植物的个主干上长出个枝干,每个枝干上再长出个小分支若在一个主干上的主干,枝干和小分支的数量之和是个,则等于( )A、 B、 C、 D、6. 若关于的方程的解是正数,则的取值范围为( )A、 B、 C、且 D、且7. 某班为奖励在数学竞赛中成绩优异的同学,花费元钱购买了甲、乙两种奖品,每种奖品至少购买件,其中甲种奖品每件元,乙种奖品每件元,则购买方案种类有( )A、种 B、种 C、种 D、种8. 如图,菱形在第二象限内, , 反比例函数的图象经过点 , 交边于点 , 若的面积为 , 则的值为( )
A、 B、 C、 D、4. 若一组数据 , , , , 的平均数为 , 则这组数据的中位数和众数分别是( )A、 , B、 , C、 , D、 ,5. 某校“研学”活动小组在一次野外实践时,发现一种植物的个主干上长出个枝干,每个枝干上再长出个小分支若在一个主干上的主干,枝干和小分支的数量之和是个,则等于( )A、 B、 C、 D、6. 若关于的方程的解是正数,则的取值范围为( )A、 B、 C、且 D、且7. 某班为奖励在数学竞赛中成绩优异的同学,花费元钱购买了甲、乙两种奖品,每种奖品至少购买件,其中甲种奖品每件元,乙种奖品每件元,则购买方案种类有( )A、种 B、种 C、种 D、种8. 如图,菱形在第二象限内, , 反比例函数的图象经过点 , 交边于点 , 若的面积为 , 则的值为( ) A、 B、 C、 D、9. 如图,在中, , 于 , 平分交于 , , 则的值为( )
A、 B、 C、 D、9. 如图,在中, , 于 , 平分交于 , , 则的值为( )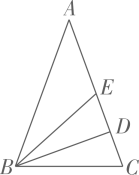 A、 B、 C、 D、10. 如图,正方形中, , 相交于点 , 平分交于点 , 把沿翻折,得到 , 是的中点,连接 , , , , 下列结论:垂直平分;;;;其中结论正确的序号是( )
A、 B、 C、 D、10. 如图,正方形中, , 相交于点 , 平分交于点 , 把沿翻折,得到 , 是的中点,连接 , , , , 下列结论:垂直平分;;;;其中结论正确的序号是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共10小题,共30.0分)
-
11. 某种芯片每个探针单元的面积为0.00000164cm2 , 0.00000164用科学记数法表示为.12. 函数y= 中自变量x的取值范围是 .13. 如图所示,正方形中,点在上,点在上,请添加一个条件: , 使≌只添一个条件即可 .
 14. 在一个不透明的盒子中装有个红球和若干个白球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是红球的概率是 , 则白球的个数是 .15. 已知不等式组无解,则的取值范围是 .16. 如图,CD是⊙O的直径,AB是弦,CD⊥AB于点E,若OA=5,AB=8,则AD的长为 .
14. 在一个不透明的盒子中装有个红球和若干个白球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是红球的概率是 , 则白球的个数是 .15. 已知不等式组无解,则的取值范围是 .16. 如图,CD是⊙O的直径,AB是弦,CD⊥AB于点E,若OA=5,AB=8,则AD的长为 . 17. 已知圆锥的底面直径为4,母线长为6,则它的侧面展开图的圆心角为度.18. 如图,在正方形中, , 是的中点,点是正方形内一个动点,且 , 连接 , 将线段绕点逆时针旋转得到线段 , 连接 , 则线段长的最小值为 .
17. 已知圆锥的底面直径为4,母线长为6,则它的侧面展开图的圆心角为度.18. 如图,在正方形中, , 是的中点,点是正方形内一个动点,且 , 连接 , 将线段绕点逆时针旋转得到线段 , 连接 , 则线段长的最小值为 . 19. 正方形ABCD的边长是8cm,点M在BC边上,且MC=2cm,P是正方形边上的一个动点,连接PB交AM于点N,当PB=AM时,PN的长是 .20. 如图,过原点的两条直线分别为: , : , 过点作轴的垂线与交于点 , 过点作轴的垂线与交于点 , 过点 , 作轴的垂线与交于点 , 过点作轴的垂线与交于点 , 过点作轴的垂线与交于点 , 依次进行下去,则点的坐标 .
19. 正方形ABCD的边长是8cm,点M在BC边上,且MC=2cm,P是正方形边上的一个动点,连接PB交AM于点N,当PB=AM时,PN的长是 .20. 如图,过原点的两条直线分别为: , : , 过点作轴的垂线与交于点 , 过点作轴的垂线与交于点 , 过点 , 作轴的垂线与交于点 , 过点作轴的垂线与交于点 , 过点作轴的垂线与交于点 , 依次进行下去,则点的坐标 .
三、解答题(本大题共8小题,共60.0分。解答应写出文字说明,证明过程或演算步骤)
-
21. 先化简再求值: , 其中 .22. 如图,在平面直角坐标系中,的三个顶点的坐标分别为 , , .
 (1)、经过平移后得到 , 已知点的坐标为 , 画出 , 并写出点 , 的坐标;(2)、画出绕点逆时针方向旋转后得到;(3)、在(2)的条件下,求线段在旋转过程中扫过的面积结果保留 .23. 若二次函数的图象经过点 , , 其对称轴为直线 , 与轴的另一交点为 .
(1)、经过平移后得到 , 已知点的坐标为 , 画出 , 并写出点 , 的坐标;(2)、画出绕点逆时针方向旋转后得到;(3)、在(2)的条件下,求线段在旋转过程中扫过的面积结果保留 .23. 若二次函数的图象经过点 , , 其对称轴为直线 , 与轴的另一交点为 . (1)、求二次函数的表达式;(2)、若点在直线上,且在第四象限,过点作轴于点 .
(1)、求二次函数的表达式;(2)、若点在直线上,且在第四象限,过点作轴于点 .①若点在线段上,且 , 求点的坐标;
②以为对角线作正方形点在右侧 , 当点在抛物线上时,求点的坐标.
24. 在一次“献爱心”捐款活动中,九年班同学人人拿出自己的零花钱,踊跃捐款,学生捐款额有元、元、元、元四种情况.根据统计数据绘制了图和图两幅尚不完整的统计图. (1)、学生捐款的众数是 ▲ , 该班共有多少名同学?(2)、请将图的统计图补充完整;并计算图中“元”所在扇形对应的圆心角度数;(3)、计算该班同学平均捐款多少元?25. 甲、乙两车在连通、、三地的公路上行驶,在、两地之间,甲车从地出发匀速向地行驶,到达地后立即按原路原速驶往地,同时乙车从地出发匀速向地行驶,到达地停留小时后,按原路原速返回到地在两车行驶的过程中,甲、乙两车距各自出发地的路程千米与甲车行驶时间小时之间的函数图象如图所示,请结合图象回答下列问题:
(1)、学生捐款的众数是 ▲ , 该班共有多少名同学?(2)、请将图的统计图补充完整;并计算图中“元”所在扇形对应的圆心角度数;(3)、计算该班同学平均捐款多少元?25. 甲、乙两车在连通、、三地的公路上行驶,在、两地之间,甲车从地出发匀速向地行驶,到达地后立即按原路原速驶往地,同时乙车从地出发匀速向地行驶,到达地停留小时后,按原路原速返回到地在两车行驶的过程中,甲、乙两车距各自出发地的路程千米与甲车行驶时间小时之间的函数图象如图所示,请结合图象回答下列问题: (1)、甲车的速度为 , 两地之间的路程为 , 并在图中内填上正确的数;(2)、求乙车从地返回到地的过程中,与之间的函数关系式;(3)、两车出发后经过多长时间距地的路程相等?直接写出答案.26. 已知四边形ABCD是正方形,等腰直角△AEF的直角顶点E在直线BC上(不与点B,C重合),FM⊥AD,交射线AD于点M.
(1)、甲车的速度为 , 两地之间的路程为 , 并在图中内填上正确的数;(2)、求乙车从地返回到地的过程中,与之间的函数关系式;(3)、两车出发后经过多长时间距地的路程相等?直接写出答案.26. 已知四边形ABCD是正方形,等腰直角△AEF的直角顶点E在直线BC上(不与点B,C重合),FM⊥AD,交射线AD于点M. (1)、当点E在边BC上,点M在边AD的延长线上时,如图①,求证:AB+BE=AM;
(1)、当点E在边BC上,点M在边AD的延长线上时,如图①,求证:AB+BE=AM;(提示:延长MF,交边BC的延长线于点H.)
(2)、当点E在边CB的延长线上,点M在边AD上时,如图②;当点E在边BC的延长线上,点M在边AD上时,如图③.请分别写出线段AB,BE,AM之间的数量关系,不需要证明;(3)、在(1),(2)的条件下,若BE= ,∠AFM=15°,则AM= .27. 为了迎接“十一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:运动鞋
价格
甲
乙
进价元双
售价元双
已知:用元购进甲种运动鞋的数量与用元购进乙种运动鞋的数量相同.
(1)、求的值;(2)、要使购进的甲、乙两种运动鞋共双的总利润利润售价进价不少于21700元,且不超过22300元,问该专卖店有几种进货方案?(3)、在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?28. 如图,在平面直角坐标系中,菱形的边在轴上,点坐标 , 点在轴正半轴上,且 , 点从原点出发,以每秒一个单位长度的速度沿轴正方向移动,移动时间为秒,过点作平行于轴的直线 , 直线扫过四边形的面积为 .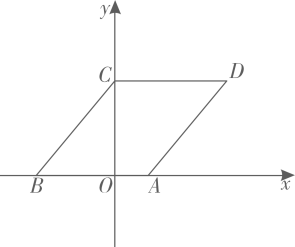 (1)、求点坐标.(2)、求关于的函数关系式.(3)、在直线移动过程中,上是否存在一点 , 使以、、为顶点的三角形是等腰直角三角形?若存在,直接写出点的坐标;若不存在,请说明理由.
(1)、求点坐标.(2)、求关于的函数关系式.(3)、在直线移动过程中,上是否存在一点 , 使以、、为顶点的三角形是等腰直角三角形?若存在,直接写出点的坐标;若不存在,请说明理由.