广西壮族自治区贵港市平南县2022-2023学年七年级下册数学期末考试试卷
试卷更新日期:2023-07-11 类型:期末考试
一、选择题(共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑.)
-
1. 冰墩墩是2022年北京冬奥会的吉祥物,如图,通过旋转后得到的图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 以下图形中,∠1和∠2不是同位角的是( )A、
2. 下列计算正确的是( )A、 B、 C、 D、3. 以下图形中,∠1和∠2不是同位角的是( )A、 B、
B、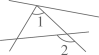 C、
C、 D、
D、 4. 如果方程组与有相同的解,则的值是( )A、2023 B、1 C、0 D、5. 计算:的结果是( )A、 B、 C、 D、6. 如图,在下列给出的条件中,不能判定的是( )
4. 如果方程组与有相同的解,则的值是( )A、2023 B、1 C、0 D、5. 计算:的结果是( )A、 B、 C、 D、6. 如图,在下列给出的条件中,不能判定的是( ) A、 B、 C、 D、7. 下列说法中不正确的有( )
A、 B、 C、 D、7. 下列说法中不正确的有( )①经过一点,有且只有一条直线与已知直线垂直
②如果两条直线被第三条直线所截,那么同旁内角互补
③经过一点,有且只有一条直线与已知直线平行
④两条平行线之间的距离是它们的公垂线段
A、1个 B、2个 C、3个 D、4个8. 光线从空气射入水中时,光线的传播方向会发生改变,这就是折射现象.如图,水面MN与底面EF平行,光线AB从空气射入水里时发生了折射,变成了光线BC射到水底C处,射线BD是光线AB的延长线,若 , , 则的度数为( ) A、 B、 C、 D、9. 《九章算术》是中国古代重要的数学著作,其中有这样一道题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗,问醇、行酒各得几何?”译文:今有醇酒(优质酒)1斗,价格50钱;行酒(勾兑酒)1斗,价格10钱.现有30钱,买2斗酒,问能买醇、行酒各多少斗?设能买醇酒x斗,行酒y斗,可列二元一次方程组为( )A、 B、 C、 D、10. 若 , , 则的值为( )A、20 B、140 C、150 D、20011. 如图,和是由分别沿着AB,AC翻折后形成的,若 , 则的度数是( )
A、 B、 C、 D、9. 《九章算术》是中国古代重要的数学著作,其中有这样一道题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗,问醇、行酒各得几何?”译文:今有醇酒(优质酒)1斗,价格50钱;行酒(勾兑酒)1斗,价格10钱.现有30钱,买2斗酒,问能买醇、行酒各多少斗?设能买醇酒x斗,行酒y斗,可列二元一次方程组为( )A、 B、 C、 D、10. 若 , , 则的值为( )A、20 B、140 C、150 D、20011. 如图,和是由分别沿着AB,AC翻折后形成的,若 , 则的度数是( )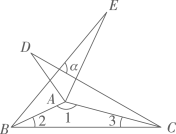 A、 B、 C、 D、12. 阅读以下材料:式子“”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为 , 这里“”是求和符号.通过对以上材料的阅读,请你计算的值为( )A、 B、 C、 D、
A、 B、 C、 D、12. 阅读以下材料:式子“”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为 , 这里“”是求和符号.通过对以上材料的阅读,请你计算的值为( )A、 B、 C、 D、二、填空题(本大题共6小题,每小题2分,共12分)
-
13. 计算:14. 因式分解15. 若 , 则16. 如图,已知梯形ABCD中, , 点E,F分别在AD,BC边上,BE和AF相交于点G,CE和DF相交于点H, , , 则阴影部分的面积为.
 17. 在日常生活中常用到密码,如取款、上网等,有一种“因式分解”法产生密码,方便记忆.如:对于多项式 , 因式分解的结果是 , 若取 , 时,则各个因式的值是: , , .于是就可以把“018162”作为一个六位数的密码,对于多项式 , 取 , 时,用上述方法产生的密码是(写出一个即可)18. 已知正方形ABCD中, , 点E在CD边上,且.将沿AE折叠至 , 延长EF交边BC于点G,连结AG、CF.若 , 则三角形CEG的周长是.
17. 在日常生活中常用到密码,如取款、上网等,有一种“因式分解”法产生密码,方便记忆.如:对于多项式 , 因式分解的结果是 , 若取 , 时,则各个因式的值是: , , .于是就可以把“018162”作为一个六位数的密码,对于多项式 , 取 , 时,用上述方法产生的密码是(写出一个即可)18. 已知正方形ABCD中, , 点E在CD边上,且.将沿AE折叠至 , 延长EF交边BC于点G,连结AG、CF.若 , 则三角形CEG的周长是.
三、解答题(本大题共8小题,满分72分.解答应写出文字说明、证明过程或演算步骤.)
-
19. 解方程组20. 先化简,再求值
, 其中
21. 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C都是格点.
⑴请画出将向左平移6个单位长度得到的;
⑵请画出关于直线MN对称的.
22. 为了促进学校阳光体育运动的发展,推进素质教育,增强学生体质,丰富校园文化,某校举行以“绳”强身健体为主题的一分钟跳绳比赛,每班选出20名同学参赛,以下是甲、乙两班同学的比赛成绩(单位:次):甲班:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.
乙班:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.
整理数据:
次数
班别
165.5~170.5
170.5~175.5
175.5~180.5
180.5~185.5
185.5~190.5
190.5~195.5
甲班
2
4
5
6
2
1
乙班
1
2
a
b
2
0
分析数据:
班别
平均数
众数
中位数
方差
甲班
180
180
43.1
乙班
180
22.6
根据以上信息,解答下列问题:
(1)、“整理数据”表格中 , ;(2)、请完成“分析数据”表格中的空缺数据;(3)、结合上述数据信息,请判断哪个班的成绩比较好,并说明理由.23. 【阅读理解】:对于形如的二次三项式,可以直接用完全平方公式把它分解成的形式.但对于二次三项式 , 就不能直接用完全平方公式分解了.我们可以添上一项1,使它与构成一个完全平方式,然后再减去1,这样整个多项式的值不变,即 ,像这样把一个二次三项式变成含有完全平方式的方法,叫做配方法.
(1)、【初步运用】请用上述方法把因式分解:
(2)、【拓展应用】已知三角形ABC的三边分别为a,b,c,且满足 , 求三角形ABC的周长.
24. 如图,在三角形ABC中,已知 , 垂足为D,DG与AC相交于点G,点E在BC上, , 垂足为F,.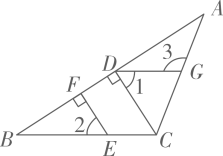 (1)、求证:;(2)、如果 , , 试说明CD平分.25. 我县是中国石硖龙眼之乡,某生态石硖龙眼园计划在龙眼收获之季租用A,B两种型号的货车将石硖龙眼运往外地销售,已知用3辆A型车和2辆B型车载满石硖龙眼一次可运18吨;用4辆A型车和5辆B型车载满石硖龙眼一次可运31吨.求:(1)、1辆A型货车和1辆B型货车满载时一次分别运石硖龙眼多少吨?(2)、若该生态园共有22吨石硖龙眼,计划租用A,B两种型号货车(每辆车都满载)一次把这批石硖龙眼运完,请问有哪几种租车方案?26. 综合与实践
(1)、求证:;(2)、如果 , , 试说明CD平分.25. 我县是中国石硖龙眼之乡,某生态石硖龙眼园计划在龙眼收获之季租用A,B两种型号的货车将石硖龙眼运往外地销售,已知用3辆A型车和2辆B型车载满石硖龙眼一次可运18吨;用4辆A型车和5辆B型车载满石硖龙眼一次可运31吨.求:(1)、1辆A型货车和1辆B型货车满载时一次分别运石硖龙眼多少吨?(2)、若该生态园共有22吨石硖龙眼,计划租用A,B两种型号货车(每辆车都满载)一次把这批石硖龙眼运完,请问有哪几种租车方案?26. 综合与实践综合与实践课上,老师让同学们“借助两条平行线AB,CD和一副直角三角板”开展数学探究活动.即:已知直线和一副直角三角板.
 (1)、【操作判断】
(1)、【操作判断】如图1,小华把一个三角板角的顶点F、G分别放在直线AB、CD上,请直接写出与的数量关系.
(2)、【迁移探究】如图2,小睿把一个三角板角的顶点F放在直线AB上,若 , 求的度数.
(3)、【拓展应用】在图1的基础上,小明把三角板角的顶点,放在E处,即(如图3),与的平分线EP,EQ分别交AB,CD于点P,Q,将含角的三角板绕点E转动,使EG始终在的内部,请问:的值是否发生变化?若不变,求出它的值;若变化,请说明理由.