(人教版)2023-2024学年八年级数学上册11.1与三角形有关的线段 同步分层训练(培优卷)
试卷更新日期:2023-07-11 类型:同步测试
一、选择题
-
1. 用12根等长的火柴棒拼成一个三角形,火柴棒不允许剩余,重叠和折断,则能摆出不同的三角形的个数是( )A、1个 B、2个 C、3个 D、4个2. 五条长度均为整数厘米的线段:a1 , a2 , a3 , a4 , a5 , 满足a1<a2<a3<a4<a5 , 其中a1=1厘米,a5=9厘米,且这五条线段中的任意三条都不能构成三角形,则a3=( )A、3厘米 B、4厘米 C、3或4厘米 D、不能确定3. 如图1, 是铁丝 的中点,将该铁丝首尾相接折成 ,且 , ,如图2.则下列说法正确的是( )
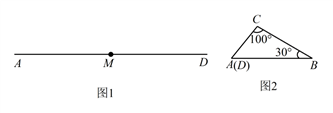 A、点 M 在 上 B、点 M 在 的中点处 C、点 M 在 上,且距点 B 较近,距点 C 较远 D、点 M 在 上,且距点 C 较近,距点 B 较远4. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE中点,且△ABC的面积等于4cm2 , 则阴影部分图形面积等于( ).
A、点 M 在 上 B、点 M 在 的中点处 C、点 M 在 上,且距点 B 较近,距点 C 较远 D、点 M 在 上,且距点 C 较近,距点 B 较远4. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE中点,且△ABC的面积等于4cm2 , 则阴影部分图形面积等于( ).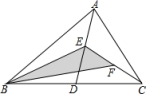 A、1cm2 B、2cm2 C、0.5cm2 D、1.5cm25. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右、向上、向右、向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到点A1 , 第2次移动到点A2……第n次移动到点An,则△OA2A2022的面积是( )
A、1cm2 B、2cm2 C、0.5cm2 D、1.5cm25. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右、向上、向右、向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到点A1 , 第2次移动到点A2……第n次移动到点An,则△OA2A2022的面积是( ) A、505m² B、 m² C、 m² D、1 009 m²6. 如图,A,B,C分别是线段A1B,B1C,C1A的中点,若△ABC的面积是1,那么△A1BlC1的面积是( )
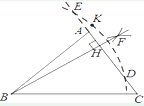
A、505m² B、 m² C、 m² D、1 009 m²6. 如图,A,B,C分别是线段A1B,B1C,C1A的中点,若△ABC的面积是1,那么△A1BlC1的面积是( )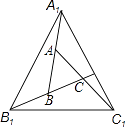 A、4 B、5 C、6 D、77. 小明用尺规作图作△ABC边AC上的高BH,作法如下:
A、4 B、5 C、6 D、77. 小明用尺规作图作△ABC边AC上的高BH,作法如下:①分别以点D,E为圆心,大于 DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
所以,BH就是所求作的高.其中顺序正确的作图步骤是( )
 A、①②③④ B、④③②① C、②④③① D、④③①②8. 要使如图的六边形框架形状稳定,至少需要添加对角线的条数是( )
A、①②③④ B、④③②① C、②④③① D、④③①②8. 要使如图的六边形框架形状稳定,至少需要添加对角线的条数是( ) A、 B、 C、 D、9. 如图,工人师傅做了一个长方形窗框 分别是四条边上的中点,为使它稳固,需要在窗框上钉一根木条,这根木条不能钉在( )
A、 B、 C、 D、9. 如图,工人师傅做了一个长方形窗框 分别是四条边上的中点,为使它稳固,需要在窗框上钉一根木条,这根木条不能钉在( )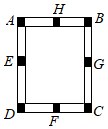 A、 两点之间 B、 两点之间 C、 两点之间 D、 两点之间10. 已知三条线段的长分别是4,4,m,若它们能构成三角形,则整数m的最大值是( )A、10 B、8 C、7 D、4
A、 两点之间 B、 两点之间 C、 两点之间 D、 两点之间10. 已知三条线段的长分别是4,4,m,若它们能构成三角形,则整数m的最大值是( )A、10 B、8 C、7 D、4二、填空题
-
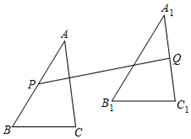
11. 如图,在 中, ,将 平移5个单位长度得到 1,点P、Q分别是 、 的中点, 的最小值等于 .
 12. 在△ABC中,若AB=5,AC=3.则中线AD的长的取值范围是。13. 如图, 分别是 的边 上的中点,连接 交于点G, , 的面积为6,设 的面积为 , 的面积为 ,则 .
12. 在△ABC中,若AB=5,AC=3.则中线AD的长的取值范围是。13. 如图, 分别是 的边 上的中点,连接 交于点G, , 的面积为6,设 的面积为 , 的面积为 ,则 .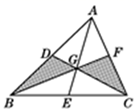 14. 如图,已知△ABC是等边三角形,点O是BC上任意一点,OE⊥AB,OF⊥AC,等边三角形的高为2,则OE+OF的值为.
14. 如图,已知△ABC是等边三角形,点O是BC上任意一点,OE⊥AB,OF⊥AC,等边三角形的高为2,则OE+OF的值为. 15. 若三角形的周长为13,且三边均为整数,则满足条件的三角形有种.
15. 若三角形的周长为13,且三边均为整数,则满足条件的三角形有种.三、解答题
-
16. 从1,2,3,…,2004中任选K-1个数中,一定可以找到能构成三角形边长的三个数(这里要求三角形三边长互不相等),试问满足条件的K的最小值是多少?
17. 如图,AD为△ABC的中线,BE为△ABD的中线.若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少? 18. 已知:△ABC中,AB=AC,BD是AC边上的中线,如果D点把三角形ABC的周长分为12cm和15cm两部分,求此三角形各边的长.
18. 已知:△ABC中,AB=AC,BD是AC边上的中线,如果D点把三角形ABC的周长分为12cm和15cm两部分,求此三角形各边的长.四、综合题
-
19. 已知:a,b,c为 的三边长.(1)、若a,b,c满足 ,试判断 的形状;(2)、化简: .20. 如图,AD为△ABC的高,AE、BF为△ABC的角平分线,若 , .
 (1)、求∠DAE的度数;(2)、若点M为线段BC上任意一点,当△BMF为直角三角形时,请直接写出∠CFM的度数.21. 如图,在平面直角坐标系中,已知点A(a , 0),B(b , 0),C(﹣1.5,-2),其中a , b满足|a+1|+(b﹣3)2=0.
(1)、求∠DAE的度数;(2)、若点M为线段BC上任意一点,当△BMF为直角三角形时,请直接写出∠CFM的度数.21. 如图,在平面直角坐标系中,已知点A(a , 0),B(b , 0),C(﹣1.5,-2),其中a , b满足|a+1|+(b﹣3)2=0. (1)、求ABC的面积;(2)、在x轴上求一点P , 使得ACP的面积与ABC的面积相等;(3)、在y轴上是否存在一点Q , 使得BCQ的面积与ABC的面积相等?若存在,请写出点Q的坐标;若不存在,请说明理由.22. 已知 的面积是 ,请完成下列问题:
(1)、求ABC的面积;(2)、在x轴上求一点P , 使得ACP的面积与ABC的面积相等;(3)、在y轴上是否存在一点Q , 使得BCQ的面积与ABC的面积相等?若存在,请写出点Q的坐标;若不存在,请说明理由.22. 已知 的面积是 ,请完成下列问题: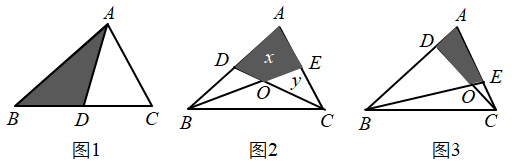 (1)、如图1所示,若 是 的 边上的中线,则 的面积 的面积.(填“ ”“ ”或“ ”)(2)、如图2所示,若 , 分别是 的 , 边上的中线,求四边形 的面积可以用如下方法:连接 ,由 得: ,同理: ,设 , 则 , .由题意得: , ,可列方程组为 ,解得 , 通过解这个方程组可得四边形 的面积为 .(3)、如图3所示, , ,请你计算四边形 的面积,并说明理由.23. 如图,在平面直角坐标系中,已知 ,其中a,b满足
(1)、如图1所示,若 是 的 边上的中线,则 的面积 的面积.(填“ ”“ ”或“ ”)(2)、如图2所示,若 , 分别是 的 , 边上的中线,求四边形 的面积可以用如下方法:连接 ,由 得: ,同理: ,设 , 则 , .由题意得: , ,可列方程组为 ,解得 , 通过解这个方程组可得四边形 的面积为 .(3)、如图3所示, , ,请你计算四边形 的面积,并说明理由.23. 如图,在平面直角坐标系中,已知 ,其中a,b满足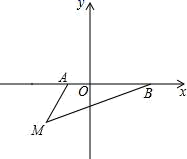 (1)、填空:a= , b=;(2)、如果在第三象限内有一点C(-2,m),请用含m的式子表示△ABC的面积;(3)、在⑵条件下,当 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
(1)、填空:a= , b=;(2)、如果在第三象限内有一点C(-2,m),请用含m的式子表示△ABC的面积;(3)、在⑵条件下,当 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.