江苏省扬州市江都区2022-2023学年八年级下学期数学期末试题

试卷更新日期：2023-07-11 类型：期末考试

进入出卷网下载

一、选择题（本大题共8小题，每小题3分，共24分.每小题只有一个选项是正确的，请将正确选项前的字母填在答题卡相应位置上）

1. 下列图形中，是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列成语描述的事件是随机事件的是（）

A、瓮中捉鳖 B、一箭双雕 C、水中捞月 D、水滴石穿

查看试题解析
3. 下列式子，属于最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{10}$ C、 $\sqrt{0.5}$ D、 $\frac{1}{\sqrt{3}}$

查看试题解析
4. 关于式子 $- \frac{1}{2} + \frac{\sqrt{3}}{2}$ 的变形，下列结果不正确的是（）

A、 $- \frac{1 + \sqrt{3}}{2}$ B、 $\frac{\sqrt{3} - 1}{2}$ C、 $- \frac{1 - \sqrt{3}}{2}$ D、 $\frac{- 1 + \sqrt{3}}{2}$

查看试题解析
5. 如图，A、B两地被池塘隔开，小强通过下面的方法估测出A、B间的距离：先在AB外选一点C，然后步测出AC、BC的中点D、E，并且步测出DE长，由此推算出AB长.若步测DE的长为50m，则A、B间的距离是（）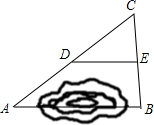

A、25m B、50m C、75m D、100m

查看试题解析
6. 已知 $P_{1} (- 1 ， y_{1})$ 、 $P_{2} (1 ， y_{2})$ 、 $P_{3} (2 ， y_{3})$ 是反比例函数 $y = \frac{k^{2} + 1}{x}$ 的图像上的三点，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{3} < y_{2}$ B、 $y_{1} < y_{2} < y_{3}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
7. 小明在学习了中心对称图形后，整理了平行四边形和特殊平行四边形之间的关系图，如图所示.从下列条件：
① $A B = A D$ ；② $A C = B D$ ；③ $A C ⊥ B D$ ；④ $A C$ 平分 $∠ D A B$ 中，选择其中一个条件填入（）处，补全关系图，其中所有正确选项的序号是（）

A、①③ B、①④ C、①③④ D、②③④

查看试题解析
8. 如图，点A是反比例函数 $y_{1} = \frac{2}{x} (x > 0)$ 图像上任意一点，过点A作 $A B / / x$ 轴，交另一个反比例函数 $y_{2} = \frac{k}{x} (k < 0 ， x < 0)$ 的图像于点B.若不论点A在何处，反比例函数 $y_{2} = \frac{k}{x} (k < 0 ， x < 0)$ 图像上总存在一点D，使四边形AOBD为平行四边形，则k的值为（）

A、-1 B、-2 C、-3 D、-4

查看试题解析

二、填空题（本大题共10小题，每小题3分，共30分.请将答案填在答题卡相应位置上）

9. 式子 $\sqrt{x + 2}$ 有意义的条件为.

查看试题解析

10. 一只不透明的袋子中装有若干个红球和白球，这些球除颜色外都相同.将这个袋中的球搅匀后从中任意摸出1个球，记下颜色后放回、搅匀，不断重复这个过程，获得如下数据：

摸球的个数n	200	300	400	500	1000	1500	2000
摸到白球的个数m	116	192	232	298	590	906	1202
摸到白球的频率 $\frac{m}{n}$	0.580	0.640	0.580	0.596	0.590	0.604	0.601

根据以上数据，估计摸到白球的概率约为（精确到0.01）.

查看试题解析

11. 如图，P为反比例函数 $y = \frac{k}{x}$ 图像的一点，过点P作 $P A ⊥ y$ 轴，垂足为点A.若 $Δ P A O$ 的面积为4，则 $k =$ .

查看试题解析
12. 如图，在 $▱ A B C D$ 中，AE平分 $∠ B A D$ ，交CD边于E， $A D = 6$ ， $E C = 4$ ，则AB的长为.

查看试题解析
13. 已知 $x = \sqrt{2} - 1$ ，则分式 $\frac{x^{2} - 2 x + 1}{x^{2} - 1}$ 的值为.

查看试题解析
14. 若一次函数 $y = x - 1$ 与反比例函数 $y = \frac{3}{x}$ 的图像交于点 $(a ， b)$ ，则 $\frac{1}{a} - \frac{1}{b} =$ .

查看试题解析
15. 三个形状、大小相同的菱形按如图的方式摆放，若 $Δ A B C$ 为正三角形，且边长为6，则一个菱形的面积为.

查看试题解析
16. 已知关于x的分式方程 $\frac{m - 1}{x + 1} = 1$ 的解是负数，则m的取值范围为.

查看试题解析
17. 如图，在矩形ABCD中， $A B = 3$ ， $A D = 5$ ，点E在DC上，将矩形ABCD沿AE折叠，点D恰好落在BC边上的点F处，那么CE的长为.

查看试题解析
18. 如图，已知线段 $A B = 10$ ，点P是AB上一动点（不与A、B重合），分别以AP、PB为边在AB的同侧作正方形APCD和PBFE，且两正方形对角线的交点分别为M、N，则MN长度的最小值为.

查看试题解析

三、解答题（本大题共10小题，共96分.请将解答过程写在答题卡相应位置上，解答时应写出必要的计算过程、推演步骤或文字说明）

19. 计算：

(1)、 $\sqrt{6} \times \sqrt{2} + \sqrt{27} \div \sqrt{9} - \sqrt{\frac{1}{3}}$ ；

(2)、 ${(\sqrt{5} - 1)}^{2} - (\sqrt{2} - 1) (\sqrt{2} + 1)$ .

查看试题解析
20. 解方程：

(1)、 $\frac{x - 3}{x - 2} + 1 = \frac{3}{2 - x}$ ；

(2)、 $\frac{x - 2}{x + 2} - \frac{x + 2}{x - 2} = \frac{16}{x^{2} - 4}$ .

查看试题解析
21. 先化简： $(\frac{x^{2} + 4}{x} - 4) \div \frac{x^{2} - 4}{x^{2} + 2 x}$ ，再从0，1，2中选择一个合适的数作为x的值代入求值.

查看试题解析
22. 某校随机调查了八年级部分学生暑假期间每天课外阅读所用的时间，并按阅读所用时间x（分钟）的范围分为四个等级： $A (20 < x \leq 40)$ ， $B (40 < x \leq 60)$ ， $C (60 < x \leq 80)$ ， $D (80 < x \leq 100)$ .根据调查得到的数据绘制了如图所示不完整的统计图.

(1)、本次调查的八年级学生共有人，在扇形统计图中， $n =$ ；

(2)、补全频数分布直方图；

(3)、若该校八年级有600名学生，请估计该校八年级每天课外阅读所用的时间超过60分钟的学生人数.

查看试题解析
23. 2023年春节科幻电影《流浪地球2》火热上映，激发了人们阅读科幻书籍的热情.某学校图书馆购进甲、乙两种科幻书籍，已知每本甲图书的进价比每本乙图书的进价高15元，购买675元甲图书的数量与购买450元乙图书的数量相同.求甲、乙两种图书每本的进价分别是多少元？

查看试题解析
24. 已知，如图，在 $Δ A B C$ 中， $A B = A C$ ， AD是BC边的中线，过点A作BC的平行线，过点B作AD的平行线，两线交于点E，连接DE交AB于点O.

(1)、求证：四边形AEBD是矩形；

(2)、若 $A B = 10$ ， $B C = 16$ ，求四边形AEDC的周长.

查看试题解析
25. 如图，已知一次函数 $y = a x + b$ 和反比例函数 $y = \frac{k}{x}$ 的图像相交于 $A (- 2 ， 1)$ 、 $B (1 ， m)$ 两点.

(1)、求一次函数和反比例函数的表达式；

(2)、结合图像，直接写出不等式 $a x + b < \frac{k}{x}$ 的解集为；

(3)、求 $Δ O A B$ 的面积.

查看试题解析
26. 观察下列各式的规律：
① $2 \sqrt{\frac{2}{3}} = \sqrt{2 + \frac{2}{3}}$ ；② $3 \sqrt{\frac{3}{8}} = \sqrt{3 + \frac{3}{8}}$ ；③ $4 \sqrt{\frac{4}{15}} = \sqrt{4 + \frac{4}{15}}$ ……

(1)、猜想：第 $n - 1$ 个等式是；

(2)、说明你的猜想的正确性；

(3)、应用：若 $a \sqrt{\frac{7}{b}} = \sqrt{a + \frac{7}{b}}$ ，则 $a + b =$ .

查看试题解析
27. 如图1，在边长为1的小正方形组成的网格中，点A、B、C、D都是格点.

(1)、点D到BC的距离为；

(2)、利用网格和无刻度的直尺作图，保留痕迹，不写作法.（友情提醒：辅助线用虚线，求作的线用实线，并加粗加黑）
①在图2中，作矩形BEDF，使得点E、F分别在BC、AD上；

②在图3中，在AB上找一点P，使得 $∠ P D A = 45 °$ ；

③在图4中，在CD上找一点M，使得MB平分 $∠ C M A$ .

查看试题解析
28. 类比一次函数和反比例函数的学习经验，某数学实验小组尝试探究“ $y = \frac{6}{| x |}$ 的函数图象与性质”，进行了如下活动.

(1)、【小组合作    讨论交流】
同学甲说：“我们可以从表达式分析，猜想图像位置.”
同学乙回应道：“是的，因为自变量x的取值范围是，所以图像与y轴不相交.”
同学丙补充说：“又因为函数值y大于0，所以图像一定在第象限.”
……

(2)、【独立操作    探究性质】
在平面直角坐标系中，画出 $y = \frac{6}{| x |}$ 的图像.
结合图像，描述函数图象与性质：
①函数 $y = \frac{6}{| x |}$ 的图像是两条曲线；
②该函数图象关于      ▲      对称；
③图像的增减性是      ▲      ；
④同学丁说：“将第二象限的曲线绕原点顺时针旋转 $90 °$ 后，与第一象限的曲线重合.”请你判断同学丁的说法是否正确？若错误，举出反例；若正确，请说明理由.

(3)、【拓展探究    综合应用】
直接写出不等式 $\frac{6}{| x |} - x > 5$ 的解集是.

查看试题解析