(人教版)2023-2024学年八年级数学上册11.1与三角形有关的线段 同步分层训练(基础卷)
试卷更新日期:2023-07-11 类型:同步测试
一、选择题
-
1. 两根长度分别为2,10的木棒,若想钉一个三角形木架,第三根木棒的长度可以是( )A、13 B、10 C、7 D、6
-
2. 若长度为x,2,3的三条线段能组成一个三角形,则x的值可能为( )A、6 B、5 C、1 D、3
-
3. 乐乐要从下面四组木棒中选择一组制作一个三角形作品,你认为他应该选( )A、3,5,6 B、2,3,5 C、2,4,7 D、3,8,4
-
4. 如图,在△ABC中,AD是△ABC的角平分线,则( )
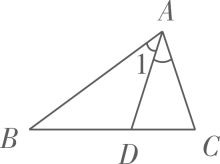 A、∠1=∠BAC B、∠1=∠ABC C、∠1=∠BAC D、∠1=∠ABC
A、∠1=∠BAC B、∠1=∠ABC C、∠1=∠BAC D、∠1=∠ABC -
5. 下列各图中,正确画出 边上的高的是( )A、
 B、
B、 C、
C、 D、
D、
-
6. 如图,直角中, , , , , 点P是线段上一动点(可与点A、点B重合),连接 , 则线段长度的取值范围是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7. 下列各个图形中,是的高的是( )A、
 B、
B、 C、
C、 D、
D、
-
8. 如图,是的中线,已知的周长为25cm,比长7cm,则的周长( )
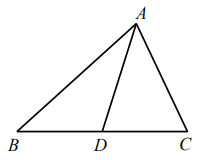 A、18cm B、22cm C、19cm D、31cm
A、18cm B、22cm C、19cm D、31cm -
9. 下列图形中,具有稳定性的是( )A、
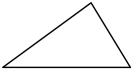 B、
B、 C、
C、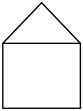 D、
D、
-
10. 桥梁的斜拉钢索是三角形的结构,主要是为了( )A、节省材料,节约成本 B、保持对称 C、利用三角形的稳定性 D、美观漂亮
二、填空题
-
11. 木工师傅在做好门框后,为了防止变形常常按如图那样钉上两根斜拉的木板条,即图中的、两根木条,其数学依据是.

-
12. 如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,设△ADC的面积为S1 , △ACE的面积为S2 , 若S△ABC=12,则S1+S2= .
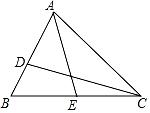
-
13. 用海伦公式求面积的计算方法是: ,其中S表示三角形的面积,a,b,c分别表示三边之长,p表示周长的一半,即 .我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致,所以这个公式也叫“海伦-秦九韶式” .请你利用公式解答下列问题.在 中,已知三边之长 , , ,则 的面积为.
-
14. 三角形的两边长分别是10和8,则第三边的x取值范围是.
-
15. 在△ABC中,若AB=4,BC=2,且AC的长为偶数,则AC= .
三、解答题
-
16. 在 中, , ,并且 为偶数,求 的周长.
-
17. 如图,AD为△ABC的中线,AB = 12cm,△ABD和△ADC的周长差是4cm,求△ABC的边AC的长(AC AB).
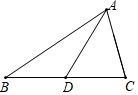
-
18. 如图,AD是△ABC的中线,AH是△ABC的高,BD=1,AH=2,求△ABC的面积.

-
19. 如图,ABCD是四根木条钉成的四边形,为了使它不变形,小明加了根木条AE,小明的做法正确吗?说说你的理由.
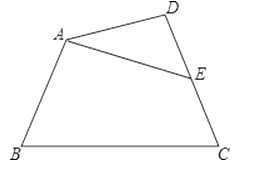
四、综合题
-
20. 若△ABC的三边长分别为m-2,2m+1,8.(1)、求m的取值范围;(2)、若△ABC的三边均为整数,求△ABC的周长.
-
21. 如图,AD,CE是△ABC的两条高;已知AD=10,CE=9,AB=12.
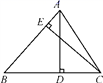 (1)、求△ABC的面积;(2)、求BC的长.
(1)、求△ABC的面积;(2)、求BC的长. -
22. 如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高。
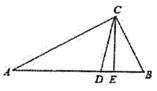 (1)、若∠A=40°,∠B=60°,求∠DCE的度数(2)、若∠A=m,∠B=n,求∠DCE.(用m、n表示)
(1)、若∠A=40°,∠B=60°,求∠DCE的度数(2)、若∠A=m,∠B=n,求∠DCE.(用m、n表示) -
23. 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,且AB=13 cm,BC=12 cm,AC=5 cm,求:
 (1)、△ABC的面积;(2)、CD的长.
(1)、△ABC的面积;(2)、CD的长.
