(北师大版)2023-2024学年八年级数学上册1.1 探索勾股定理 同步测试
试卷更新日期:2023-07-11 类型:同步测试
一、选择题
-
1. 如图,在中,平分交AC于点D,且 , F在BC上,E为AF的中点,连接DE,若 , , , 则AB的长为( )
 A、 B、 C、 D、92. 如图是高空秋千的示意图,小明从起始位置点A处绕着点O经过最低点B,最终荡到最高点C处,若 , 点A与点B的高度差AD=1米,水平距离BD=4米,则点C与点B的高度差CE为( )
A、 B、 C、 D、92. 如图是高空秋千的示意图,小明从起始位置点A处绕着点O经过最低点B,最终荡到最高点C处,若 , 点A与点B的高度差AD=1米,水平距离BD=4米,则点C与点B的高度差CE为( ) A、4米 B、4.5米 C、5米 D、5.5米3. 如图,在△ABC中,AB=AC=10,BC=12,AD平分∠BAC,则AD等于( )
A、4米 B、4.5米 C、5米 D、5.5米3. 如图,在△ABC中,AB=AC=10,BC=12,AD平分∠BAC,则AD等于( ) A、6 B、7 C、8 D、94. 如图,在长方形纸片ABCD中,AB=8cm,AD=6cm.把长方形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,则AF的长为( )
A、6 B、7 C、8 D、94. 如图,在长方形纸片ABCD中,AB=8cm,AD=6cm.把长方形纸片沿直线AC折叠,点B落在点E处,AE交DC于点F,则AF的长为( ) A、 cm B、 cm C、7cm D、 cm5. 如图,在中, , 分别以A,C为圆心,大于长为半径作弧,两弧相交于点M,N,作直线 , 与 , 分别交于D,E,连接 , 若 , , 则的周长为( )
A、 cm B、 cm C、7cm D、 cm5. 如图,在中, , 分别以A,C为圆心,大于长为半径作弧,两弧相交于点M,N,作直线 , 与 , 分别交于D,E,连接 , 若 , , 则的周长为( ) A、16 B、17 C、18 D、196. 如图,长方形纸片ABCD中,AD=4,AB=10,按如图的方式折叠,使点B与点D重合,折痕为EF,则DE长为( )
A、16 B、17 C、18 D、196. 如图,长方形纸片ABCD中,AD=4,AB=10,按如图的方式折叠,使点B与点D重合,折痕为EF,则DE长为( ) A、4.8 B、5 C、5.8 D、67. 如图,在直线l上有正方形a,b,c,若a,c的面积分别为4和16,则b的面积为( )
A、4.8 B、5 C、5.8 D、67. 如图,在直线l上有正方形a,b,c,若a,c的面积分别为4和16,则b的面积为( ) A、24 B、20 C、12 D、228. 在等腰中, , , 则底边上的高为( )A、12 B、 C、 D、189. 如图所示,已知中, , , 于 , 为上任一点,则 等于( )
A、24 B、20 C、12 D、228. 在等腰中, , , 则底边上的高为( )A、12 B、 C、 D、189. 如图所示,已知中, , , 于 , 为上任一点,则 等于( )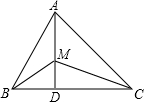 A、9 B、35 C、45 D、无法计算10. 如图,在中, , 于点D,E是上一点,且 , 若 , , 则的长为( )
A、9 B、35 C、45 D、无法计算10. 如图,在中, , 于点D,E是上一点,且 , 若 , , 则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
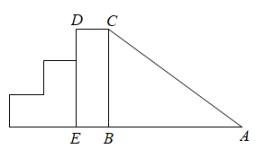
11. 如图是一个滑梯示意图,左边是楼梯,右边是滑道,已知滑道与的长度相等,滑梯的高度 , .则滑道的长度为m.
 12. 如图,在Rt△ABC中,AC=4,AB=5,∠C=90°,BD平分∠ABC交AC于点D,则BD的长是.
12. 如图,在Rt△ABC中,AC=4,AB=5,∠C=90°,BD平分∠ABC交AC于点D,则BD的长是. 13. 如图所示的衣架可以近似看成一个等腰三角形ABC,其中 , 底边BC的长 , 那么衣架的高.
13. 如图所示的衣架可以近似看成一个等腰三角形ABC,其中 , 底边BC的长 , 那么衣架的高.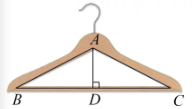 14. 如图,在长方形纸片中, , , 点M为上一点,将沿翻至 , 交于点G,交于点F,且 , 则的长度是.
14. 如图,在长方形纸片中, , , 点M为上一点,将沿翻至 , 交于点G,交于点F,且 , 则的长度是.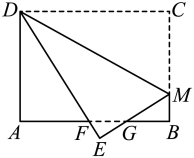 15. 如图,在Rt△ABC中,∠B=90°,分别以A,C为圆心,大于AC长为半径画弧,两弧相交于点M,N,作直线MN,与AC,BC分别交于点D,点E,连结AE,当AC=13,AB=5时,则△ABE的周长是.
15. 如图,在Rt△ABC中,∠B=90°,分别以A,C为圆心,大于AC长为半径画弧,两弧相交于点M,N,作直线MN,与AC,BC分别交于点D,点E,连结AE,当AC=13,AB=5时,则△ABE的周长是.
三、解答题
-
16. 如图,某校攀岩墙的顶部A处安装了一根安全绳 , 让它垂到地面时比墙高多出了2米,教练把绳子的下端C拉开8米后,发现其下端刚好接触地面(即米), , 求攀岩墙的高度.
 17. 如图,已知在Rt△ABC中,∠ACB=90°,AC=9,BC=12,AB的垂直平分线交AB于点D,交BC于点E,连结AE,求BE的长.
17. 如图,已知在Rt△ABC中,∠ACB=90°,AC=9,BC=12,AB的垂直平分线交AB于点D,交BC于点E,连结AE,求BE的长. 18. 如图,中, , , AD平分∠BAC交BC于点D,分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于点M和点N,连接MN,交AD于点E,求AE的长.
18. 如图,中, , , AD平分∠BAC交BC于点D,分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于点M和点N,连接MN,交AD于点E,求AE的长.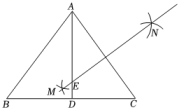 19. 如图,在中, , 平分 , 已知 , , 求的长.
19. 如图,在中, , 平分 , 已知 , , 求的长.
四、综合题
-
20. 如图,点A在直线l上,在直线l右侧做等腰三角形 , , , 点D与点B关于直线l轴对称,连接交直线l于点E,连接.
 (1)、求证:;(2)、求证:;(3)、当时,求证:.21. 如图,在中, , 平分交于点D,作于点E.
(1)、求证:;(2)、求证:;(3)、当时,求证:.21. 如图,在中, , 平分交于点D,作于点E. (1)、若 , 求的度数;(2)、若 , , 求的面积.22. 在中, , , , 点D为边上的一个动点,连接 , 点A关于直线的对称点为点E,直线交于点F.
(1)、若 , 求的度数;(2)、若 , , 求的面积.22. 在中, , , , 点D为边上的一个动点,连接 , 点A关于直线的对称点为点E,直线交于点F. (1)、如图1,当时,根据题意将图形补充完整,并直接写出的度数;(2)、如图2,当时,用等式表示线段之间的数量关系,并证明.23. 【问题背景】
(1)、如图1,当时,根据题意将图形补充完整,并直接写出的度数;(2)、如图2,当时,用等式表示线段之间的数量关系,并证明.23. 【问题背景】 (1)、如图1,点P是线段 , 的中点,求证:;(2)、【变式迁移】
(1)、如图1,点P是线段 , 的中点,求证:;(2)、【变式迁移】
如图2,在等腰中,是底边上的高线,点E为内一点,连接 , 延长到点F,使 , 连接 , 若 , 若 , , 求的长;(3)、【拓展创新】
如图3,在等腰中, , , 点D为中点,点E在线段上(点E不与点B,点D重合),连接 , 过点A作 , 连接 , 若 , , 请直接写出的长.