北师大版数学九年级上册同步练习——第一章《特殊平行四边形》2.矩形的性质与判定(3)
试卷更新日期:2023-07-11 类型:同步测试
一、选择题
-
1. 下列叙述错误的是( )A、平行四边形的对角线互相平分 B、矩形的对角线相等 C、对角线互相平分的四边形是平行四边形 D、对角线相等的四边形是矩形2. 如图,在平面直角坐标系中,将长方形沿直线折叠(点E在边上),折叠后顶点D恰好落在边上的点F处.若点D的坐标为 . 则点E的坐标为( )
 A、 B、 C、 D、3. 如图,矩形中,点、分别为边、上两动点,且 , , 沿翻折矩形,使得点恰好落在边(含端点)上,记作点 , 翻折后点对应点 , 则的最小值为( )
A、 B、 C、 D、3. 如图,矩形中,点、分别为边、上两动点,且 , , 沿翻折矩形,使得点恰好落在边(含端点)上,记作点 , 翻折后点对应点 , 则的最小值为( ) A、 B、 C、 D、24. 如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E, , 则的度数为( )
A、 B、 C、 D、24. 如图,在矩形ABCD中,对角线AC、BD相交于点O,交BD于点E, , 则的度数为( ) A、40° B、35° C、30° D、25°5. 如图,矩形ABCD中,AD=3,AB=4,M为线段BD上一动点,MP⊥CD于点P,MQ⊥BC于点Q,则PQ的最小值是( )
A、40° B、35° C、30° D、25°5. 如图,矩形ABCD中,AD=3,AB=4,M为线段BD上一动点,MP⊥CD于点P,MQ⊥BC于点Q,则PQ的最小值是( ) A、 B、3 C、 D、6. 如图,直线 , 平分 , , 且平移恰好到 , 则下列结论:①平分;②;③平分;④.其中一定正确的结论有( )
A、 B、3 C、 D、6. 如图,直线 , 平分 , , 且平移恰好到 , 则下列结论:①平分;②;③平分;④.其中一定正确的结论有( ) A、1个 B、2个 C、3个 D、4个7. 如图,在中, , 且 , , 点D是斜边上的一个动点,过点D分别作于点M,于点N,连接 , 则线段的最小值为( )
A、1个 B、2个 C、3个 D、4个7. 如图,在中, , 且 , , 点D是斜边上的一个动点,过点D分别作于点M,于点N,连接 , 则线段的最小值为( ) A、5 B、3.6 C、2.4 D、4.8
A、5 B、3.6 C、2.4 D、4.8二、填空题
-
8. 平行四边形的对角线与相交于点 , 若要使平行四边形成为矩形,则需要添加的一个条件是 . (只写出一种情况即可)9. 木工师傅要做一张长方形的桌面.完成后,量得桌面的长为 , 宽为 , 对角线为130cm,则做出的这个桌面.(填“合格”或“不合格”)10. 如图,在中相交于点 , , 当时,是矩形.
 11. 如图, △ABC的边BC长为4cm.将△ABC平移2cm得到△A′B′C′ ,且BB′⊥BC,则阴影部分的面积为 .
11. 如图, △ABC的边BC长为4cm.将△ABC平移2cm得到△A′B′C′ ,且BB′⊥BC,则阴影部分的面积为 .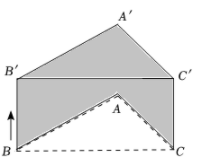 12. 如图,BE,BF分别是与它的邻补角的平分线, , 垂足为点E, , 垂足为点F,EF分别交边AB,AC于点M和N.若 , , 则的长为 .
12. 如图,BE,BF分别是与它的邻补角的平分线, , 垂足为点E, , 垂足为点F,EF分别交边AB,AC于点M和N.若 , , 则的长为 .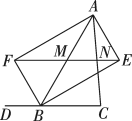 13. 如图,在矩形中, , 点在边上,且 , 、分别是边、上的动点,且 , 是线段上的动点,连接 , 若则线段的长为 .
13. 如图,在矩形中, , 点在边上,且 , 、分别是边、上的动点,且 , 是线段上的动点,连接 , 若则线段的长为 .
三、解答题
-
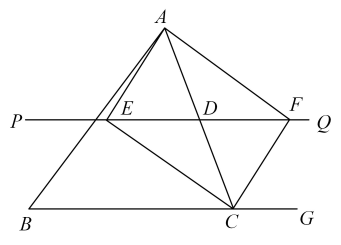
14. 如图所示,已知直线MN//PQ,直线AC交MN、PQ于点A、C,所得的同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.试猜想AC与BD的关系,并说明理由.
 15. 如图,已知平行四边形ABCD中,E是BC的中点,连接AE并延长,交DC的延长线于点F , 且AF=AD , 连接BF , 求证:四边形ABFC是矩形.
15. 如图,已知平行四边形ABCD中,E是BC的中点,连接AE并延长,交DC的延长线于点F , 且AF=AD , 连接BF , 求证:四边形ABFC是矩形.