江苏省扬州市宝应县2022-2023学年七年级下学期数学期末试题
试卷更新日期:2023-07-11 类型:期末考试
一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项前的字母代号填涂在答题卡相应位置上)
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 如果 ,那么下列不等式正确的是( )A、 B、 C、 D、3. 下列多边形具有稳定性的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,在方格纸中,点是正方形网格的格点.若 , 则点可能是( )
4. 如图,在方格纸中,点是正方形网格的格点.若 , 则点可能是( )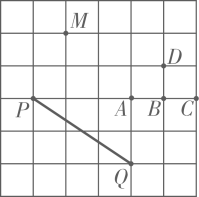 A、点 B、点 C、点 D、点5. 已知直线 , 将含角的直角三角板按如图所示摆放.若 , 则的度数是( )
A、点 B、点 C、点 D、点5. 已知直线 , 将含角的直角三角板按如图所示摆放.若 , 则的度数是( )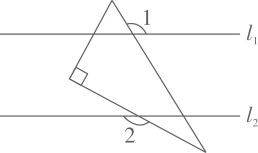 A、 B、 C、 D、6. 下列因式分解正确的是( )A、 B、 C、 D、7. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空,”诗中后面两句的意思是:如果一间客房住?人,那么有7人无房可住:如果一间客房住9人,那么就空出一间客房,若设该店有客房间,房客人,则列出关于的二元一次方程组正确的是( )A、 B、 C、 D、8. 关于的不等式组有且只有三个整数解,则的最大值是( )A、3 B、4 C、5 D、6
A、 B、 C、 D、6. 下列因式分解正确的是( )A、 B、 C、 D、7. 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空,”诗中后面两句的意思是:如果一间客房住?人,那么有7人无房可住:如果一间客房住9人,那么就空出一间客房,若设该店有客房间,房客人,则列出关于的二元一次方程组正确的是( )A、 B、 C、 D、8. 关于的不等式组有且只有三个整数解,则的最大值是( )A、3 B、4 C、5 D、6二、填空题(本大题共有10小题,每小题3分,共30分.不需写出解答过程,请把答案直接填写在答题卡相应位置上)
-
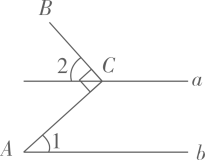
9. 科学家在实验室中检测出某种病毒的直径约为0.000000103米,将数据0.000000103用科学记数法表示为 .10. 因式分解: .11. 请写出命题“如果 , 那么”的逆命题是 .12. 已知 , 则 .13. 若一个多边形的每个内角均为 , 则这个多边形的边数为 .14. 若等腰三角形的两边长分别是和 , 则这个等腰三角形的周长是 .15. 如图,直线 , 点分别在直线上, , 若 , 则的度数为 .
 16. 如图,将沿直线方向平移后得到 , 已知 , 则平移的距离是 .
16. 如图,将沿直线方向平移后得到 , 已知 , 则平移的距离是 .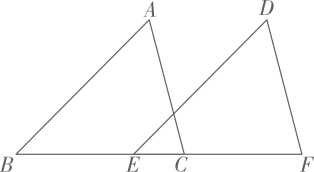 17. 一个盒子里有若干个大小相同的白球和红球,从中摸到1个红球得4分,摸到1个白球得3分,王俊凯同学摸到了个红球,个白球,共得32分,如果把他摸到的一组红球和白球的数量表示为的形式,那么为 .18. 如图,长方形的周长为8,分别以长方形的一条长和一条宽向外作两个正方形,且这两个正方形的面积和为10,则长方形的面积是 .
17. 一个盒子里有若干个大小相同的白球和红球,从中摸到1个红球得4分,摸到1个白球得3分,王俊凯同学摸到了个红球,个白球,共得32分,如果把他摸到的一组红球和白球的数量表示为的形式,那么为 .18. 如图,长方形的周长为8,分别以长方形的一条长和一条宽向外作两个正方形,且这两个正方形的面积和为10,则长方形的面积是 .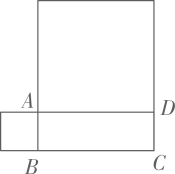
三、解答题(本大题共有9小题,共96分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)
-
19. 计算:(1)、;(2)、 .20.(1)、解方程组:;(2)、解不等式 .21. 已知 , 求的值.22. 整式的值为 .
 (1)、当时,求的值;(2)、若的取值范围如图所示,求的非正整数值.23. 如图,直线 , 且直线被直线所截.
(1)、当时,求的值;(2)、若的取值范围如图所示,求的非正整数值.23. 如图,直线 , 且直线被直线所截.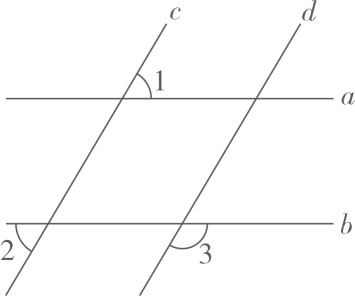 (1)、求证:;(2)、若 , 试判断直线与直线的位置关系,并说明理由.24. 如图1,将长为 , 宽为的大长方形分割成四个完全相同的直角三角形,拼成“赵爽弦图”(如图),得到大小两个正方形.
(1)、求证:;(2)、若 , 试判断直线与直线的位置关系,并说明理由.24. 如图1,将长为 , 宽为的大长方形分割成四个完全相同的直角三角形,拼成“赵爽弦图”(如图),得到大小两个正方形.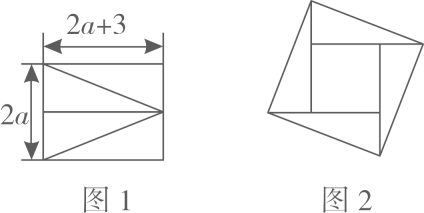 (1)、用关于的代数式表示图1中大长方形的面积;(2)、求图2中小正方形的面积是多少(结果要化简)?25. 如图,是的角平分线, , 交于点 .
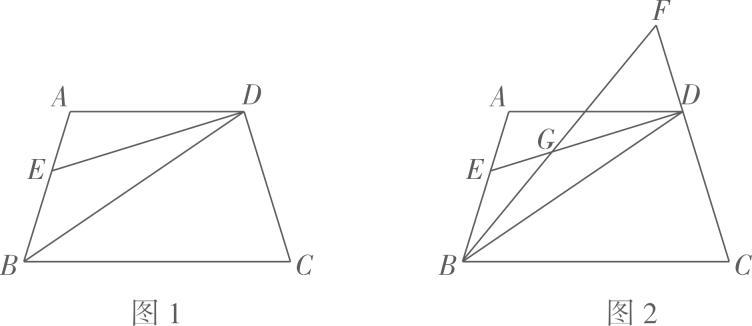
(1)、用关于的代数式表示图1中大长方形的面积;(2)、求图2中小正方形的面积是多少(结果要化简)?25. 如图,是的角平分线, , 交于点 .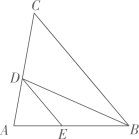 (1)、求证:;(2)、若 , , 求的度数.26. 在解二元一次方程组时,我们常常也会采用了一种“整体代入消元”的方法将二元一次方程组转化为一元一次方程求解,比如,解方程组 , 首先将方程②变形得 , 即③,其次把方程①代入③得:即 , 最后把代入方程①,得 , 所以方程组的解为 .
(1)、求证:;(2)、若 , , 求的度数.26. 在解二元一次方程组时,我们常常也会采用了一种“整体代入消元”的方法将二元一次方程组转化为一元一次方程求解,比如,解方程组 , 首先将方程②变形得 , 即③,其次把方程①代入③得:即 , 最后把代入方程①,得 , 所以方程组的解为 .请你解决以下问题:
(1)、你能否尝试用“整体代入消元”的方法解方程组;(2)、已知满足方程组;(Ⅰ)求的值;
(Ⅱ)求出这个方程组的所有整数解.