2023年人教版数学四升五暑期衔接训练：第6讲 三角形
试卷更新日期：2023-07-10 类型：复习试卷
一、单选题
-
1. 用下面（ ）组长度的线段可以围成三角形。
① 3 cm、 5 cm、 8 cm；② 4 cm、 4 cm、 8 cm；③ 4 cm、 4 cm、 6 cm；④ 4 cm、 7 cm、 8 cm
A、①②③ B、②③④ C、①③④ D、③④2. 李爷爷元宵节做了花灯。花灯底部如图，如果想再增加一根木条使底部框架更牢固。下面方法最合理的是（ ）。
A、
B、
C、
D、
3. 一个等腰三角形，一条边长8厘米，另一条边长4厘米，第三条边长（ ）厘米。A、4 B、8 C、12 D、164. 如图，2个相同的直角三角形拼成一个大三角形，拼成的大三角形的内角和是（ ）。
A、360° B、90° C、180° D、无法确定5. 东东要把一根长10cm的铁丝分成三段，然后用这三段铁丝首尾连接围成一个三角形。他在2cm处剪一刀，如果请你剪第二刀（取整厘米），可以在（ ）的位置剪。
A、5cm B、6cm C、7cm D、8cm6. 数学课上，小英和小丽两人都用长为4cm、5cm 和6cm的小棒各摆一个三角形（首尾相接），他们两人所摆的三角形（ ）。A、形状不相同，大小不相等 B、形状不相同，大小相等 C、形状相同，大小不相等 D、形状相同，大小相等7. 三角形PQR是一个直角三角形，且角R为直角。RQ线段比线段PR长，N为线段PR的中点，且M为线段PQ的中点。符合上面叙述的三角形是（ ）。A、
B、
C、
D、
8. 如果一个三角形中最小的一个内角大于45°，那么这个三角形是（ ）三角形。A、锐角 B、直角 C、钝角 D、无法确定二、填空题
-
9. 一个三角形三条边的长度分别是4cm、5cm、5cm，按边分类这个三角形是三角形，当最短边增加1cm后，这个三角形变成三角形，这时它每个角是°。10. 观察下图，再算一算。∠1= ， ∠2=。
11. 一个三角形，其中两条边长分别是6厘米、4厘米，第三条边长最长是 ， 最短是。（取整厘米数）12. 如图，等腰三角形的底角∠1=°。若将图中等腰三角形对折剪开，能得到两个完全一样的三角形。
13. 在一个三角形中，有两个内角分别是36°和74°，第三个内角是°，这个三角形按角分是一个三角形。14. 下图是一个等腰三角形，∠1+∠2=∠3+∠4，∠1=∠2，∠3=∠4，那么∠5=。
15. 在一个直角三角形中，其中一个内角是45°，那么另一个内角是度，它还是一个三角形。16. 如图，是由三个大小不同的等边三角形组成的，AB长厘米。从点A经点C到点B的长度是厘米，从点A经点D、点F和点E，最后到点B的长度是厘米。
17. 如果一个三角形中，一个角的度数等于另两个角的度数之和，那么这个三角形一定是三角形。18. 王叔叔把一根18分米长的铁丝正好折成了一个正三角形铁框，每边长分米，要折成一条腰是5分米的等腰三角形铁框，铁框底边长分米。现在这个铁框的顶角是110°，两个底角都是°。19. 如图1、图2，将一张正方形纸按提示的方法折，那么三角形AGC按边分是 三角形。你判断的方法是 。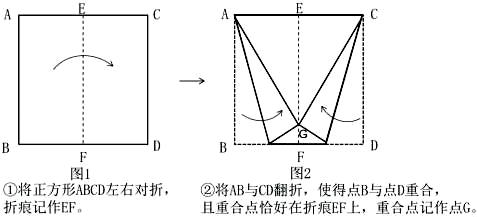
20. 丽州广场将举办放风筝比赛，天天的爸爸准备用一根长16分米的小竹条做一个等腰三角形的风筝架（边长是整分米数），他可以有种做法。三、作图题
-
21. 根据已有的三角形画出等腰三角形。（图中三角形分别是两个等腰三角形的一半）。
22. 在一个街心公园的角落处，缺少一个三角形花坛，请你设计出一个三角形花坛的平面图，并画出它的一条高，标出相对应的底。我画的是（ ）三角形。
四、计算题
-
23. 已知∠1=120°，三角形ABC是直角三角形，三角形ABD是等腰三角形，求∠2和∠3的度数。
24. 如图，三角形ABC和三角形DBC都是等腰三角形，求∠3的度数。（注意：∠A=90°）
五、解决问题
-
25. 红红家有一块三角形的小菜园，菜园的最大角是120°，且最大角的度数是最小角的4倍，这块三角形菜地其他角的度数是多少？26. 在能摆成三角形的小棒下面画“√”。（单位：cm）
三根小棒必m须符合（ ），才能摆成三角形。
27.
(1)、如图，∠1=°，∠2=° 。(2)、小刚想给他的小狗做一个房子，房顶的框架要做成三角形，其中一根木条长3dm，另一根木条长5dm，那么第三根木条最长是dm，最短是dm。（取整分米数。）28. 小明家有一块三角形的菜地，菜地的最大角是120°，且最大角的度数是最小角的4倍。
(1)、这块三角形菜地其它角的度数是多少？(2)、如果从小明家到菜地，有如图三条路线，你会选择哪一条？为什么？
