北师大版数学九年级上册同步练习——第一章《特殊平行四边形》2.矩形的性质与判定（2）
试卷更新日期：2023-07-10 类型：同步测试
一、选择题
-
1. 已知 中，下列条件：① ；② ；③ ；④ 平分 ，其中能说明 是矩形的是（ ）A、① B、② C、③ D、④2. 一个木匠要制作矩形的踏板，他在一个对边平行的长木板上分别沿与长边垂直的方向锯了两次，就能得到矩形的踏板，这样做最直接的道理是（ ）
A、有两个角是直角的四边形是矩形 B、有三个角是直角的四边形是矩形 C、对角线相等的平行四边形是矩形 D、一组对边平行且相等的四边形是矩形.3. 已知：在△ABC中，AC=BC，点D、E分别是边AB、AC的中点，延长DE至点F，使得EF=DE，那么四边形AFCD一定是（ ）A、菱形 B、矩形 C、直角梯形 D、等腰梯形4. 如图，在平行四边形ABCD中，在不添加任何辅助线的情况下，添加以下哪个条件，能使平行四边形ABCD是矩形（ ）
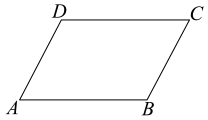A、 B、 C、 D、5. 如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连结EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（ ）
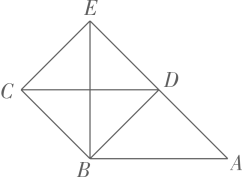A、AB=BE B、CE⊥DE C、∠ADB=90° D、BE⊥AB6. 顺次联结四边形各边中点所得的四边形是矩形，那么四边形一定是（ ）A、菱形 B、对角线相等的四边形 C、对角线互相垂直的四边形 D、对角线互相垂直且平分的四边形7. 如图，在四边形ABCD中，点E，F，G，H分别是AD，BD，BC，CA的中点，若四边形EFGH是矩形，则四边形ABCD需满足的条件是（ ）
A、 B、 C、 D、8. 问题背景：如图，AD是的中线，四边形是平行四边形．讨论交流：小明说：“若 ， 则四边形是矩形．”
小强说：“若 ， 则四边形是菱形．”
下列说法中正确的是（ ）
A、小明不对，小强对 B、小明对，小强不对 C、小明和小强都对 D、小明和小强都不对二、填空题
-
9. 如图，在平行四边形中，对角线与相交于点 ， 点 ， 在上，且 ， 连接 ， ， ， ． 若添加一个条件使四边形是矩形，则该条件可以是 ． （填写一个即可）
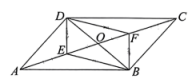10. 在平行四边形ABCD中，对角线AC，BD交于点O，只需添加一个条件，即可证明平行四边形ABCD是矩形，这个条件可以是（写出一个即可）．11. 如图，在平行四边形 中，对角线 、 相交于点O，在不添加任何辅助线的情况下，请你添加一个条件 ， 使平行四边形 是矩形．
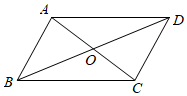12. 如图，一个平行四边形的活动框架，对角线是两根橡皮筋．若改变框架的形状，则∠α也随之变化，两条对角线长度也在发生改变．当∠α为度时，两条对角线长度相等．
13. 如图，四边形为平行四边形，延长至 ， 使 ， 连接 ， ， ， 若添加一个条件后，使四边形成为矩形，则添加的条件是 ．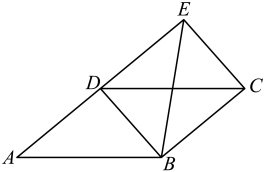
14. M为矩形ABCD中AD的中点，P为BC上一点，PE⊥MC，PF⊥MB，当AB、BC满足时，四边形PEMF为矩形.三、解答题
-
15. 如图，过的顶点A分别作及其外角的平分线的垂线，垂足分别为E、F，求证：四边形是矩形；
16. 如图，在菱形中，对角线 ， 相交于点O，过点B作 ， 且 ， 连接 ， 求证：四边形是矩形．
17. 如图，O是菱形ABCD对角线的交点，作DE∥AC，CE∥BD，DE、CE交于点E，四边形OCED是矩形吗？说说你的理由．
