北师大版数学九年级上册同步练习——第一章《特殊平行四边形》2.矩形的性质与判定(1)
试卷更新日期:2023-07-10 类型:同步测试
一、选择题
-
1. 如图,平行四边形中,下列说法一定正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
2. 如图所示,在矩形中, , 与相交于点O,下列说法正确的是( )
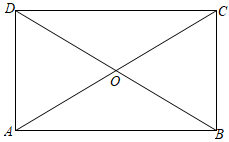 A、点O为矩形的对称中心 B、点O为线段的对称中心 C、直线为矩形的对称轴 D、直线为线段的对称轴
A、点O为矩形的对称中心 B、点O为线段的对称中心 C、直线为矩形的对称轴 D、直线为线段的对称轴 -
3. 矩形、菱形都具有的性质是( )A、对角线互相平分 B、对角线互相垂直 C、对角线平分一组对角 D、对角线相等
-
4. 如图,矩形ABCD中,AB=8,AD=4,点E、F分别是AB、DC上的动点,EF∥BC,则AF+CE的最小值是( )
 A、8 B、12 C、8 D、16
A、8 B、12 C、8 D、16 -
5. 如图,ABCD是一张长方形纸片,且AD=2CD.沿过点D的折痕将A角翻折,使得点A落在BC上(如图中的点A′),折痕交AB于点G,则∠ADG=( )
 A、30° B、15° C、75° D、22.5°
A、30° B、15° C、75° D、22.5° -
6. 如图,四边形的四个顶点分别在矩形的边和对角线上,已知 , 下列条件能使四边形是平行四边形的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7. 如图,在矩形纸片中, , , 将矩形纸片折叠,使点B与点D重合,折痕为 , 则四边形的周长为( )
 A、40 B、43 C、48 D、53
A、40 B、43 C、48 D、53 -
8. 如图,在矩形中,、相交于点 , 平分交于点 . 若 , 则的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
9. 如图,在矩形ABCD中,E,F分别是BC,AE的中点,若 , , 则DF的长是 .

-
10. 出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一、如图,在矩形中, , , 对角线与交于点O,点E为边上的一个动点, , , 垂足分别为点F,G,则 .

-
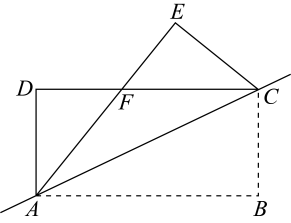
11. 如图,矩形ABCD中, , . 在边AD上取一点E,使 , 过点C作 , 垂足为点F,则BF的长为 .
-
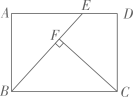
12. 如图,点E为矩形ABCD的边BC长上的一点,作DF⊥AE于点F,且满足DF=AB.下面结论:①△DEF≌△DEC;②S△ABE = S△ADF;③AF=AB;④BE=AF.其中正确的结论是 .

-
13. 在矩形中,点E在边上,点F在边上,连接若 , , 则的长为 .
-
14. 如图,在矩形ABCD中, , 点E在边AB上, , 连接DE,将沿着DE翻折,点A的对应点为P,连接EP、DP,分别交边BC于点F、G,如果 , 那么CG的长是 .