重庆市忠县2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-07-10 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，是无理数的是（）

A、 $\sqrt{7}$ B、 $\sqrt{4}$ C、 $- \frac{22}{7}$ D、 $0.101001$

查看试题解析
2. 已知点A（a，b），若a＜0，b＞0，则A点一定在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 根据如图数轴上表示，其解集是（）

A、 $- 2 < x \leq 8$ B、 $- 2 \leq x < 8$ C、 $- 2 < x < 8$ D、 $- 2 \leq x \leq 8$

查看试题解析
4. 下列事件中适合采用抽样调查的是（）

A、了解七年级（1）班学生的数学期末考试成绩 B、“神16”（神舟十六号飞船）发射前的零部件检查 C、对某流行性疾病患者的“密切接触者”进行医学调查 D、了解忠县青少年学生对卫生防疫知识的掌握情况

查看试题解析
5. 如图，点E在线段AB的延长线上，下列条件中能判断 $A B ∥ C D$ 的是（）

A、 $∠ A + ∠ 1 + ∠ 4 = 180 °$ B、 $∠ 3 = ∠ 4$ C、 $∠ A = ∠ E B C$ D、 $∠ 1 = ∠ 2$

查看试题解析
6. 下列命题是真命题的个数是（）
①过直线外一点有且只有一条直线与已知直线平行；②垂直于同一条直线的两直线互相垂直；③平行于同一条直线的两直线互相平行；④同位角相等；⑤一个角的两边分别与另一个角的两边平行，那么这两个角相等；⑥从直线外一点到这条直线上的点连成的线段中垂线段的长度最短．

A、2个 B、3个 C、4个 D、5个

查看试题解析
7. 估计 $5 \sqrt{2} - 1$ 的值在（）

A、4到5之间 B、5到6之间 C、6到7之间 D、7到8之间

查看试题解析
8. 《九章算术》记载：“三只雀五只燕，共重16两；互换一只，恰同重．问雀、燕一只各几何？”设每只雀、燕分别重x两、y两，则列方程组为（）

A、 ${\begin{array}{l} 3 x + 5 y = 16 \\ 4 x + y = x + 5 y \end{array}$ B、 ${\begin{array}{l} 3 x + 5 y = 16 \\ 2 x + y = x + 4 y \end{array}$ C、 ${\begin{array}{l} x + y = 16 \\ 3 x + y = x + 5 y \end{array}$ D、 ${\begin{array}{l} x + y = 16 \\ 2 x + y = x + 4 y \end{array}$

查看试题解析
9. 已知 $a > b > c$ 且 $x > y > z$ ，则下列各式中最小的是（）

A、 $a x + b y + c z$ B、 $a y + b x + c z$ C、 $a z + b x + c y$ D、 $a z + b y + c x$

查看试题解析
10. 已知平面直角坐标系中质点从点 $A_{0} (1 ， 0)$ 出发，第1次向上移动1个单位后往逆时针转 $90 °$ 方向作第2次移动，第n（n为正整数）次移动n个单位后往逆时针转 $90 °$ 方向作第 $n + 1$ 次移动．设质点第n次移动后到达点 $A_{n}$ ，则点 $A_{2023}$ 为（）

A、 $(1013 ， 1013)$ B、 $(1013 ， - 1012)$ C、 $(- 1011 ， - 1012)$ D、 $(- 1011 ， 1011)$

查看试题解析

二、填空题

11. 实数 $- \sqrt{2}$ ， $- \sqrt{3}$ ， $- 1$ ， $1 - \sqrt{2}$ 中最小的数是．

查看试题解析
12. 2023年奥林匹克日用数字20230623表示，这组数字中出现频数最高的数是．

查看试题解析
13. 若方程组 ${\begin{array}{l} 3 x + 4 y = 2 k \\ 2 x - 3 y = - 2 \end{array}$ 的解满足 $5 x + y < 2$ ，则实数k的取值范围是．

查看试题解析
14. 如图，已知直线 $A B ∥ C D$ ，点E是线段 $A B$ 的中点，若 $△ A E D$ 的面积为5，则 $△ A B C$ 的面积为．

查看试题解析
15. 如图，已知 $A C > 5 c m$ ，将 $△ A B C$ 沿 $A C$ 方向平移5cm，得到 $△ D E F$ ，连接 $B E$ ，若 $△ A B C$ 的周长为27cm，则阴影部分的周长为cm．

查看试题解析
16. 如图长方形 $A B C D$ 由图1、2、3、4、5拼成，设图1、2、3是边长分别为a，b，c $(a < b < c)$ 的正方形，图4是长方形，图5是正方形．对于判断：① $a + b > c$ ；②图4的周长为 $3 b + c$ ；③ $a + c = 2 b$ ；④长方形 $A B C D$ 的周长为 $2 (a + b + c)$ ，其中正确的是（填编号）．

查看试题解析
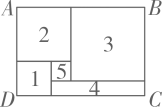17. 若关于x的不等式组 ${\begin{array}{l} \frac{3 x + 4}{6} - \frac{4 x - 1}{4} \geq 1 \\ 2 x + a < 5 x + 1 \end{array}$ 有且只有2个负整数解，且关于x，y的方程组 ${\begin{array}{l} a x + y = 11 \\ 3 x - y = 1 \end{array}$ 有整数解，则整数 $a =$ ．

查看试题解析
18. 对于千位数字是a、百位数字是b、十位数字是c、个位数字是d的四位正整数M，若 $a + c = b + d = 11$ ，则称这个四位正整数M为“平衡数”，并记 $f (M) = \frac{a - c}{b - d}$ ， $G (M) = 10 a + b - (10 c + d)$ ．例如：对于四位正整数2497，∵ $2 + 9 = 4 + 7 = 11$ ， ∴2497是“平衡数”，且 $f (2497) = \frac{2 - 9}{4 - 7} = \frac{7}{3}$ ， $G (2497) = 24 - 97 = - 73$ ．若四位正整数M是一个“平衡数”，且满足 $a < b$ ， $f (M) = - 1$ ， $G (M)$ 是7的整数倍，则 $M =$ ．

查看试题解析

三、解答题

19. 计算：

(1)、 $| 1 - \sqrt{2} | - \sqrt{{(- 3)}^{2} + {(- 2)}^{2}}$ ；

(2)、 $\sqrt{64} - | - 2 | + \sqrt[3]{- 27} - {(- \frac{1}{3})}^{0}$

查看试题解析
20. 解下面各题：

(1)、解方程组 ${\begin{array}{l} \frac{x - 2}{2} + \frac{y + 6}{3} = 3 \\ 2 x + 3 y = 13 \end{array}$ ；

(2)、解不等式组： ${\begin{array}{l} 5 (x + 1) > 2 x - 1 \\ \frac{2 (x + 3)}{3} \geq x + 1 \end{array}$ ，并把它的解集用数轴表示出来．

查看试题解析
21. 如图，在平面直角坐标系中，已知 $△ A B C$ 的顶点 $A (- 1 ， 3)$ ， $B (- 3 ， - 2)$ ， $C (1 ， - 1)$ ，若将 $△ A B C$ 先向右平移4个单位长度，再向下平移2个单位长度得到 $△ A_{1} B_{1} C_{1}$ ，且A、B、C的对应点分别是 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ ．

(1)、画出 $△ A_{1} B_{1} C_{1}$ ，直接写出点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 的坐标；

(2)、若 $△ A B C$ 的边上有一点 $G (m ， n)$ 经过上述平移后的对应点为 $G_{1}$ ，写出点 $G_{1}$ 的坐标；

(3)、求 $△ A_{1} B_{1} C_{1}$ 的面积

查看试题解析
22. 本期，张老师组织七年级学生开展了A、B、C、D四个数学实践活动，张老师从七年级学生中随机抽取部分学生进行问卷调查，要求每名学生从四个活动中选择一个自己最喜欢的活动，根据调查结果绘制成如图所示的两幅不完整的统计图，请你根据图中信息解答下列问题：

(1)、求参加此次问卷调查的学生人数：

(2)、在扇形统计图中，求扇形B的圆心角的度数，并将条形统计图补充完整；

(3)、若学校七年级学生共有800名，请估计七年级学生中最喜欢活动B的人数．

查看试题解析
23. 已知实数a的平方根为 $2 x + 1$ ， $1 - 7 x$ ， $\sqrt{17}$ 的整数部分为b．

(1)、求a，b的值；

(2)、若 $\sqrt{17}$ 的小数部分为c，求 $25 a - {(b + c)}^{2}$ 的平方根．

查看试题解析
24. 为创建足球特色学校，某中学决定开设“足球大课间活动”，购买了“双星牌”足球 $40$ 个，“李宁牌”足球 $25$ 个，共花费 $10500$ 元．已知“李宁牌”足球的单价比“双星牌”足球的单价高30元．

(1)、求两种品牌足球的单价各多少元？

(2)、根据学校发展需要，该中学决定再次购进两种品牌的足球 $80$ 个，恰好赶上经销商搞“优惠促销”活动，其中“双星牌”足球单价打 $8$ 折，“李宁牌”足球单价优惠 $30$ 元．如果此次学校购买两种品牌足球的总费用不能超过 $10560$ 元，且购买“双星牌”的足球不能多于 $50$ 个，请问有几种购买方案？学校最好选择哪种方案？说明理由．

查看试题解析
25. 如图所示，已知 $A D ∥ B C$ ， $∠ A = ∠ D C B$ ，点E是线段 $A D$ 上的一点， $∠ A B C$ 的平分线与 $∠ E C D$ 的平分线相交于点F，连接 $C E$ ．

(1)、证明： $A B ∥ C D$ ；

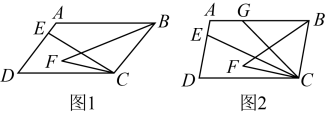(2)、若三角形的三内角之和为180°，证明： $2 ∠ F + ∠ E C B = 180 °$ ；

(3)、如图2，设 $∠ B C F$ 的平分线交AB于点G，若 $∠ D = ∠ D E C$ ，求 $∠ F C G$ 的大小．

查看试题解析
26. 为便于夜间航行船只查看长江航道及河床两岸的情况，长江航道管理局在如图所示MN水域地带的两岸M、N处分别安置了一盏可以不断匀速旋转地探照灯．设N水域地带两岸 $A B ∥ C D$ ，点N处探照灯射出的光线自 $N D$ 开始顺时针旋转，点M处探照灯射出的光线自 $M B$ 开始顺时针旋转，当两灯射出的光线旋转至各自岸边时立即反向旋转，旋转中常常出现交叉照射，若点N处射出的光线每秒旋转a度，点M处射出的光线每秒旋转b度．且 $\sqrt{{(2 a - 5 b)}^{2}} + | a + b - 7 | = 0$ ．

(1)、求a，b的值；

(2)、如图2，设两灯同时开始旋转，点N处探照灯射出的光线在旋转到NC之前，若两盏探照灯射出的光线在点F处交叉照射，是否存在点F使得过F作 $F E ⊥ N F$ 交 $A B$ 于点E，且 $∠ M F E = 30 °$ ，若存在，求 $∠ M N F$ 的度数；若不存在，说明理由．

(3)、设点M处探照灯先旋转15秒后，点N处探照灯才开始一起旋转，记两盏灯一起旋转的时间为t秒．当点M处探照灯射出的光线首次旋转至 $M A$ 位置之前，能否出现两盏探照灯射出的光线互相平行，若能，直接写出所有的值；若不能，说明理由．

查看试题解析