重庆市开州区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-07-10 类型:期末考试
一、单选题
-
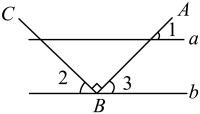
1. 实数 的相反数是( )A、 B、 C、2 D、2. 9的平方根是( )A、 B、3 C、 D、3. 如图, , 且 , 若 , 则的大小为( )
 A、 B、 C、 D、4. 以下调查中,适宜全面调查的是( )A、调查某批次汽车的抗撞击能力 B、调查某班学生的视力情况 C、调查春节联欢晚会的收视率 D、了解武汉市中学生课外阅读情况5. 若 , 则下列不等式的变形错误的是( )A、 B、 C、 D、6. 观察如图所示的一系列图形,它们是按一定规律排列的,依照此规律,第九个图中“○”的个数为( )
A、 B、 C、 D、4. 以下调查中,适宜全面调查的是( )A、调查某批次汽车的抗撞击能力 B、调查某班学生的视力情况 C、调查春节联欢晚会的收视率 D、了解武汉市中学生课外阅读情况5. 若 , 则下列不等式的变形错误的是( )A、 B、 C、 D、6. 观察如图所示的一系列图形,它们是按一定规律排列的,依照此规律,第九个图中“○”的个数为( ) A、26 B、28 C、30 D、327. 不等式组的解集在数轴上表示正确的是( )A、
A、26 B、28 C、30 D、327. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、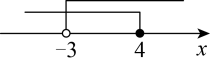 D、
D、 8. 《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少?设有人,辆车,可列方程组为( )A、 B、 C、 D、9. 下列说法中,正确的是( )A、直线外一点到这条直线的垂线段叫做点到直线的距离 B、过一点有且只有一条直线与已知直线平行 C、立方根等于本身的数只有和1 D、若 , 且 , 则点在第三象限10. 已知关于x,y的方程组 , 给出下列说法:
8. 《孙子算经》是中国古代重要的数学著作,成书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车;若每辆车乘坐2人,则有9人步行.问人与车各多少?设有人,辆车,可列方程组为( )A、 B、 C、 D、9. 下列说法中,正确的是( )A、直线外一点到这条直线的垂线段叫做点到直线的距离 B、过一点有且只有一条直线与已知直线平行 C、立方根等于本身的数只有和1 D、若 , 且 , 则点在第三象限10. 已知关于x,y的方程组 , 给出下列说法:①当时,方程组的解也是的解;
②若 , 则;
③无论a取何值,x,y的值不可能互为相反数;
④x,y都为自然数的解有5对.
以上说法中正确的个数为( )
A、1 B、2 C、3 D、4二、填空题
-
11. 计算: .12. 若点在x轴上,则m的值为 .13. 已知a为整数,且 , 则 .14. 在画频数分布直方图时,一个样本容量为90的样本,最小值为40,最大值为131.若确定组距为9,则分成的组数是 .15. 如图, , 相交于点O,平分 , , 则 .
 16. 如图,将长方形纸片沿折叠后,点 , 分别落在 , 的位置,再沿边将折叠到处,已知 , 则 .
16. 如图,将长方形纸片沿折叠后,点 , 分别落在 , 的位置,再沿边将折叠到处,已知 , 则 .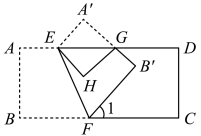 17. 若不等式的解都能使不等式成立,则实数a的取值范围是 .18. 若一个四位正整数(各个数位均不为0),百位数字比千位数字小3,个位数字比十位数字小2,则称该数为“和平数”,例如:4131,9642都是“和平数”,将一个四位正整数的百位和十位交换位置后得到四位数 , 若为“和平数”,且能被9整除,则满足条件的所有值中,的最大值是 .
17. 若不等式的解都能使不等式成立,则实数a的取值范围是 .18. 若一个四位正整数(各个数位均不为0),百位数字比千位数字小3,个位数字比十位数字小2,则称该数为“和平数”,例如:4131,9642都是“和平数”,将一个四位正整数的百位和十位交换位置后得到四位数 , 若为“和平数”,且能被9整除,则满足条件的所有值中,的最大值是 .三、解答题
-
19. 计算:(1)、(2)、20. 解二元一次方程组:(1)、(2)、21. 阅读下列推理过程,完成下面的证明.
已知:如图,已知 , 垂足分别为D、F, . 求证: .
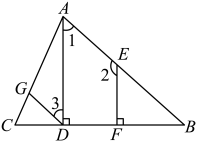
证明:(已知)
( )
( )
▲ ( )
又( )
▲ ( )
▲ ( )
( )
22. 为积极响应教育部“停课不停学”的号召,某小学组织本校教师开展线上教学,为了解学生线上教学的学习效果,决定随机抽取六年级部分学生进行质量测评,以下是根据测试的数学成绩绘制的统计图表:成绩分组统计表
段数
成绩x/分
人数(频数)
第1段
4
第2段
12
第3段
18
第4段
a
第5段
30
成绩分布情况

请根据以上信息,解答下列问题:
(1)、此次抽样的样本容量为 , ;(2)、扇形统计图中,第5段对应的圆心角度数为;(3)、已知该年级有1000名学生参加测试,请估计该年级数学成绩为优秀(80分及以上)的人数.23. 如图,在边长为1个单位长度的小正方形组成的网格中,三角形的顶点均在格点上,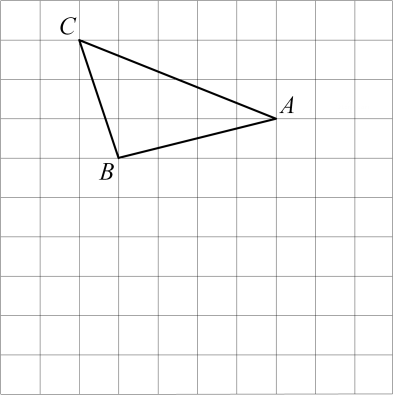 (1)、请建立合适的平面直角坐标系,使点的坐标分别为和 , 此时点的坐标为;(2)、在(1)的条件下:将三角形沿格线进行2次平移,平移后得到三角形 , 且点的坐标为 .
(1)、请建立合适的平面直角坐标系,使点的坐标分别为和 , 此时点的坐标为;(2)、在(1)的条件下:将三角形沿格线进行2次平移,平移后得到三角形 , 且点的坐标为 .①请说出是如何进行平移的:;
②点的坐标为 , 并在图中画出三角形 .
24. 某文具店准备从批发市场购买若干排球和书包(每个排球的价格相同,每个书包的价格相同),若购买4个排球和8个书包共需920元;若购买9个排球和6个书包共需1170元.(1)、每个排球和书包各需多少元?(2)、根据需要,文具店一次性购买排球和书包共60个,实际购买中得知:在此批发市场购买排球和书包的总数量超过50时,书包打八折出售(排球仍按原价出售)如果此次用于购买排球的费用不超过购买书包的费用,那么最多可以购买多少个排球?25. 已知:直线 , 点A、点C分别在直线、直线上,点B在之间,连接、 .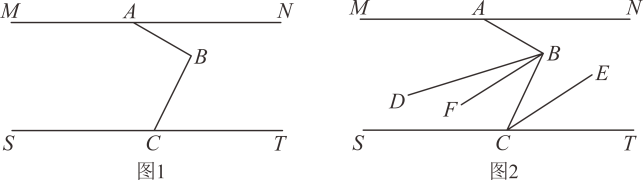 (1)、如图1,请写出的关系,并给出证明;(2)、如图2,利用(1)中的结论解决问题:若 , 平分 , 平分 , , 求的度数.26.
(1)、如图1,请写出的关系,并给出证明;(2)、如图2,利用(1)中的结论解决问题:若 , 平分 , 平分 , , 求的度数.26.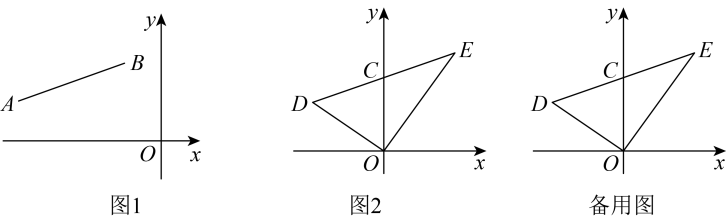 (1)、如图1,在平面直角坐标系中,满足 . 直接写出a、b的值:;;(2)、如图2,在(1)问条件下将线段向右平移,平移后A、B的对应点分别为D、E,线段交y轴于点C,当和面积相等时,求点D、点E的坐标;(3)、在(2)问的条件下,延长交x轴于点F,点F的坐标为 , 过点E作直线轴,动点P从点E沿直线l以每秒2个单位长度的速度向左运动,同时动点Q从点F沿x轴以每秒个单位的速度向右运动,当最小时,直接写出三角形的面积.
(1)、如图1,在平面直角坐标系中,满足 . 直接写出a、b的值:;;(2)、如图2,在(1)问条件下将线段向右平移,平移后A、B的对应点分别为D、E,线段交y轴于点C,当和面积相等时,求点D、点E的坐标;(3)、在(2)问的条件下,延长交x轴于点F,点F的坐标为 , 过点E作直线轴,动点P从点E沿直线l以每秒2个单位长度的速度向左运动,同时动点Q从点F沿x轴以每秒个单位的速度向右运动,当最小时,直接写出三角形的面积.