（人教版）2023-2024学年七年级数学上册2.2 整式的加减同步分层训练（培优卷）

试卷更新日期：2023-07-10 类型：同步测试

进入出卷网下载

一、选择题

1. 将图1中周长为32的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形，并将它们按图2的方式放入周长为48的长方形中，则没有覆盖的阴影部分的周长为（）

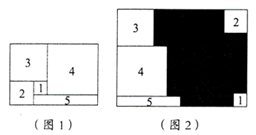A、16 B、24 C、30 D、40

查看试题解析
2. 为求1+2+2²+2³+…+2²⁰¹⁵的值，可令S=1+2+2²+2³+…+2²⁰¹⁵ ，则2S=2+2²+2³+…+2²⁰¹⁶ ，因此2S﹣S=2²⁰¹⁶﹣1.仿照以上推理，计算出1+5+5²+5³+…+5²⁰¹⁵的值为（）

A、5²⁰¹⁵﹣1 B、5²⁰¹⁶﹣1 C、 $\frac{5^{2015} - 1}{4}$ D、 $\frac{5^{2016} - 1}{4}$

查看试题解析
3. 已知有理数 $a$ ， $b$ ， $c$ 在数轴上的位置如图，且 $| c | > | a | > | b |$ ，则 $| a + b | - 2 | c - b | + | a + c | =$ （）．

A、 $c - b$ B、0 C、 $3 b - 3 c$ D、 $2 a + 3 b - c$

查看试题解析
4. 如图，在一个长方形中放入三个正方形，从大到小正方形的边长分别为 $a$ 、 $b$ 、 $c$ ，则右上角阴影部分的周长与左下角阴影部分周长差为（）

A、a+b B、 $b + c$ C、 $2 a$ D、 $2 b$

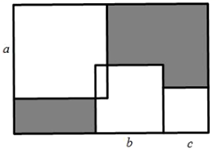查看试题解析
5. 如果 $a 、 b 、 c 、 d$ 为互不相等的有理数，且 $| a - c | = | b - c | = | d - b | = 2$ ，那么 $| a - d | =$ （）

A、8 B、6 C、4 D、2

查看试题解析
6. 将1，2，3，4，5，6六个数随机分成2组，每组各3个，分别用 $a_{1}$ ， $a_{2}$ ， $a_{3}$ 和 $b_{1}$ ， $b_{2}$ ， $b_{3}$ 表示，且 $a_{1} < a_{2} < a_{3}$ ， $b_{1} > b_{2} > b_{3}$ ，设 $m = | a_{1} - b_{1} | + | a_{2} - b_{2} | + | a_{3} - b_{3} |$ ，则 $m$ 的可能值为（）.

A、 $3$ B、 $3 或 9$ C、 $9$ D、 $5 或 9$

查看试题解析
7. 设实数a，b，c满足a＞b＞c(ac＜0)，且|c|＜|b|＜|a|，则|x-a|+|x+b|+|x-c|的最小值为（）

A、 $\frac{| a + b + c |}{3}$ B、|b| C、a+b D、－c－a

查看试题解析
8. 已知a＜-b，且 $\frac{a}{b}$ ＞0，化简|a|-|b|+|a+b|+|ab|=（）

A、2a+2b+ab B、-ab C、-2a-2b+ab D、-2a+ab

查看试题解析
9. 已知代数式x²＋ax－2y＋7－(bx²－2x＋9y－1)的值与x的取值无关，则a＋b的值为（）

A、－1 B、1 C、－2 D、2

查看试题解析
10. 把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为mcm，宽为ncm)的盒子底部(如图②)盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是（）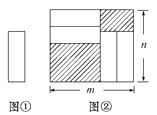

A、4mcm B、4ncm C、2(m+n)cm D、4(m-n)cm

查看试题解析

二、填空题

11. 如图，用三个同（1）图的长方形和两个同（2）图的长方形用两种方式去覆盖一个大的长方形 $A B C D$ ，两种方式未覆盖的部分（阴影部分）的周长一样，那么（1）图中长方形的面积 $S_{1}$ 与（2）图长方形的面积 $S_{2}$ 的比是.

查看试题解析
12. 点 $A$ 、 $B$ 在数轴上分别表示有理数 $a$ 、 $b$ ，则在数轴上 $A$ 、 $B$ 两点之间的距离为 $A B = | a - b |$ ，利用数轴上两点间距离，可以得到 $| x + 1 | - | x - 3 |$ 的最大值是．

查看试题解析
13. $a$ 、 $b$ 、 $c$ 在数轴上的位置如图所示：试化简 $| a - b | - 2 c - | c + b | + | 3 b | =$ .

查看试题解析
14. 把四张大小相同的长方形卡片（如图①）按图②、图③两种放法放在一个底面为长方形（长比宽多6）的盒底上，底面未被卡片覆盖的部分用阴影表示，若记图②中阴影部分的周长为C₂ ，图③中阴影部分的周长为C₃ ，则C₂-C₃=.

查看试题解析
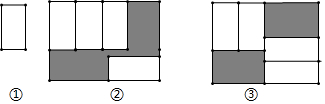15. 已知 $a < - 1$ ， $- 1 \leq c \leq 0$ ， $a < b < c$ ，则 $| a + b + c | - | b - c | - | a - c - 1 |$ 的最小值为，最大值为.

查看试题解析

三、解答题

16. 小亮在计算一个多项式与 $3 x^{2} - 2 x + 7$ 的差时，因误以为是加上 $3 x^{2} - 2 x + 7$ 而得到答案 $5 x^{2} + 2 x + 4$ ，请求出这个问题的正确答案.

查看试题解析
17. 已知A=a²-2ab+b² ， B=-a²-3ab-b²,求：2A-3B。

查看试题解析
18. 已知2m-4与3m-1是一个正数的平方根，且 $- \frac{1}{2}$ a^2x-3b⁸ 与3a⁷b^5+y是同类项，求m+x+y的算术平方根．

查看试题解析
19. 若x，y为非零有理数，且 $x = | y |$ ，y＜0，化简： $| y |$ ＋ $| - 2 y |$ － $| 3 y - 2 x |$ －2y.

查看试题解析

四、综合题

20. 如图，数轴上的点A，B，C分别表示有理数a，b，c，其中b是最小的正整数，且a，b，c满足(c-5)²+|a+b|=0．

(1)、a= ， b= ， c=

(2)、P为线段BC上的一个动点，点P表示的数为x，化简：|x-b|-|x-c|．

(3)、点A，B，C开始在数轴上运动，点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和每秒5个单位长度的速度向右运动，t秒后，我们用AB表示点A与点B之间的距离，用BC表示点B与点C之间的距离．探究：BC-AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求出BC-AB的值．

查看试题解析
21. 已知口，⋆、△分别代表1∼9中的三个自然数．

(1)、如果用⋆△表示一个两位数，将它的个位和十位上的数字交换后得到一个新的两位数Δ⋆，若⋆Δ与Δ⋆的和恰好为某自然数的平方，则该自然数是；

(2)、如果在一个两位数⋆Δ前揷入一个数口后得到一个三位数口⋆△，设⋆△代表的两位数为x，口代表的数为y，则三位数口⋆Δ用含x，y的式子可表示为；

(3)、设a表示一个两位数，b表示一个三位数，把a放在b的左边组成一个五位数m，再把b放在a的左边、组成一个新五位数n．试探索：m-n能否被9整除？并说明你的理由．

查看试题解析
22. 七年级学习代数式求值时，遇到这样一类题“代数式 $a x - y + 6 + 3 x - 5 y - 1$ 的值与 $x$ 的取值无关，求 $a$ 的值”，通常的解题方法是：把x、y看作字母，a看作系数合并同类项，因为代数式的值与x的取值无关，所以含 $x$ 项的系数为0，
即原式＝ $(a + 3) x - 6 y + 5$ ，所以 $a + 3 = 0$ ，则 $a = - 3$ ．

(1)、若关于 $x$ 的多项式 $(2 x - 3) m + 2 m^{2} - 3 x$ 的值与 $x$ 的取值无关，求 $m$ 值；

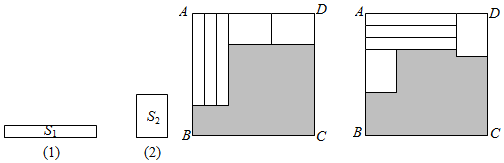
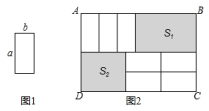(2)、已知A $= 2 x^{2} + 3 x y - 2 x - 1$ ， B $= - x^{2} + x y - 1$ ；且3A＋6B的值与 $x$ 无关，求 $y$ 的值；

(3)、7张如图1的小长方形，长为a，宽为b，按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分（图中阴影部分），设右上角的面积为 $S_{1}$ ，左下角的面积为 $S_{2}$ ，当AB的长变化时， $S_{1} - S_{2}$ 的值始终保持不变，求 $a$ 与 $b$ 的等量关系．

查看试题解析
23. 如图，在数轴上点A，B，C表示的数分别为﹣2，1，6，点A与点B之间的距离表示为AB，点B与点C之间的距离表示为BC，点A与点C之间的距离表示为AC.

(1)、则AB＝， BC＝， AC＝.

(2)、点A，B，C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.请问：BC﹣AB的值是否随着运动时间t的变化而改变？若变化，请说明理由；若不变求其值.

查看试题解析

（人教版）2023-2024学年七年级数学上册2.2 整式的加减 同步分层训练（培优卷）

一、选择题

二、填空题

三、解答题

四、综合题

（人教版）2023-2024学年七年级数学上册2.2 整式的加减同步分层训练（培优卷）