山东省济宁市2023年中考数学试卷
试卷更新日期:2023-07-10 类型:中考真卷
一、单选题
-
1. 实数中无理数是( )A、 B、0 C、 D、1.52. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列各式运算正确的是( )A、 B、 C、 D、4. 若代数式有意义,则实数的取值范围是( )A、 B、 C、 D、且5. 如图,是直尺的两边, , 把三角板的直角顶点放在直尺的边上,若 , 则的度数是( )
3. 下列各式运算正确的是( )A、 B、 C、 D、4. 若代数式有意义,则实数的取值范围是( )A、 B、 C、 D、且5. 如图,是直尺的两边, , 把三角板的直角顶点放在直尺的边上,若 , 则的度数是( ) A、 B、 C、 D、6. 为检测学生体育锻炼效果,从某班随机抽取10名学生进行篮球定时定点投篮检测,投篮进球数统计如图所示.对于这10名学生的定时定点投篮进球数,下列说法中错误的是( )
A、 B、 C、 D、6. 为检测学生体育锻炼效果,从某班随机抽取10名学生进行篮球定时定点投篮检测,投篮进球数统计如图所示.对于这10名学生的定时定点投篮进球数,下列说法中错误的是( ) A、中位数是5 B、众数是5 C、平均数是5.2 D、方差是27. 下列各式从左到右的变形,因式分解正确的是( )A、 B、 C、 D、8. 一个几何体的三视图如下,则这个几何体的表面积是( )
A、中位数是5 B、众数是5 C、平均数是5.2 D、方差是27. 下列各式从左到右的变形,因式分解正确的是( )A、 B、 C、 D、8. 一个几何体的三视图如下,则这个几何体的表面积是( ) A、 B、 C、 D、9. 如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点均在小正方形方格的顶点上,线段交于点 , 若 , 则等于( )
A、 B、 C、 D、9. 如图,在正方形方格中,每个小正方形的边长都是一个单位长度,点均在小正方形方格的顶点上,线段交于点 , 若 , 则等于( ) A、 B、 C、 D、10. 已知一列均不为1的数满足如下关系: , , 若 , 则的值是( )A、 B、 C、 D、2
A、 B、 C、 D、10. 已知一列均不为1的数满足如下关系: , , 若 , 则的值是( )A、 B、 C、 D、2二、填空题
-
11. 一个函数过点 , 且随增大而增大,请写出一个符合上述条件的函数解析式 .12. 已知一个多边形的内角和为540°,则这个多边形是边形.13. 某数学活动小组要测量一建筑物的高度,如图,他们在建筑物前的平地上选择一点 , 在点和建筑物之间选择一点 , 测得 . 用高的测角仪在处测得建筑物顶部的仰角为 , 在处测得仰角为 , 则该建筑物的高是 .
 14. 已知实数满足 , 则 .15. 如图,是边长为6的等边三角形,点在边上,若 , , 则 .
14. 已知实数满足 , 则 .15. 如图,是边长为6的等边三角形,点在边上,若 , , 则 .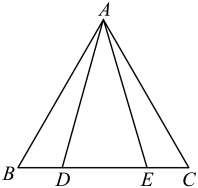
三、解答题
-
16. 计算: .17. 某学校为扎实推进劳动教育,把学生参与劳动教育情况纳入积分考核.学校随机抽取了部分学生的劳动积分(积分用x表示)进行调查,整理得到如下不完整的统计表和扇形统计图.
等级
劳动积分
人数
A
4
B
m
C
20
D
8
E
3

请根据以上图表信息,解答下列问题:(1)、统计表中 , C等级对应扇形的圆心角的度数为;(2)、学校规定劳动积分大于等于80的学生为“劳动之星”.若该学校共有学生2000人,请估计该学校“劳动之星”大约有多少人;(3)、A等级中有两名男同学和两名女同学,学校从A等级中随机选取2人进行经验分享,请用列表法或画树状图法,求恰好抽取一名男同学和一名女同学的概率.18. 如图,是矩形的对角线. (1)、作线段的垂直平分线(要求:尺规作图,保留作图㢃迹,不必写作法和证明);(2)、设的垂直平分线交于点 , 交于点 , 连接 .
(1)、作线段的垂直平分线(要求:尺规作图,保留作图㢃迹,不必写作法和证明);(2)、设的垂直平分线交于点 , 交于点 , 连接 .①判断四边形的形状,并说明理由;
②若 , 求四边形的周长.
19. 如图,正比例函数和反比例函数的图像交于点 . (1)、求反比例函数的解析式;(2)、将直线向上平移3个单位后,与轴交于点 , 与的图像交于点 , 连接 , 求的面积.20. 为加快公共领域充电基础设施建设,某停车场计划购买A,B两种型号的充电桩.已知A型充电桩比B型充电桩的单价少万元,且用万元购买A型充电桩与用万元购买B型充电桩的数量相等.(1)、A,B两种型号充电桩的单价各是多少?(2)、该停车场计划共购买个A,B型充电桩,购买总费用不超过万元,且B型充电桩的购买数量不少于A型充电桩购买数量的 . 问:共有哪几种购买方案?哪种方案所需购买总费用最少?21. 如图,已知是的直径, , 切于点 , 过点作交于点 , 若 .
(1)、求反比例函数的解析式;(2)、将直线向上平移3个单位后,与轴交于点 , 与的图像交于点 , 连接 , 求的面积.20. 为加快公共领域充电基础设施建设,某停车场计划购买A,B两种型号的充电桩.已知A型充电桩比B型充电桩的单价少万元,且用万元购买A型充电桩与用万元购买B型充电桩的数量相等.(1)、A,B两种型号充电桩的单价各是多少?(2)、该停车场计划共购买个A,B型充电桩,购买总费用不超过万元,且B型充电桩的购买数量不少于A型充电桩购买数量的 . 问:共有哪几种购买方案?哪种方案所需购买总费用最少?21. 如图,已知是的直径, , 切于点 , 过点作交于点 , 若 . (1)、如图1,连接 , 求证:;(2)、如图2,是上一点,在上取一点 , 使 , 连接 . 请问:三条线段有怎样的数量关系?并证明你的结论.22. 如图,直线交轴于点 , 交轴于点 , 对称轴为的抛物线经过两点,交轴负半轴于点 . 为抛物线上一动点,点的横坐标为 , 过点作轴的平行线交抛物线于另一点 , 作轴的垂线 , 垂足为 , 直线交轴于点 .
(1)、如图1,连接 , 求证:;(2)、如图2,是上一点,在上取一点 , 使 , 连接 . 请问:三条线段有怎样的数量关系?并证明你的结论.22. 如图,直线交轴于点 , 交轴于点 , 对称轴为的抛物线经过两点,交轴负半轴于点 . 为抛物线上一动点,点的横坐标为 , 过点作轴的平行线交抛物线于另一点 , 作轴的垂线 , 垂足为 , 直线交轴于点 .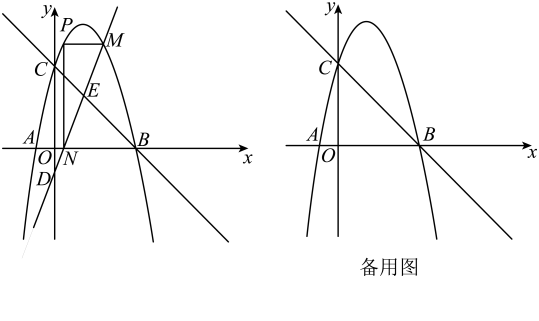 (1)、求抛物线的解析式;(2)、若 , 当为何值时,四边形是平行四边形?(3)、若 , 设直线交直线于点 , 是否存在这样的值,使?若存在,求出此时的值;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若 , 当为何值时,四边形是平行四边形?(3)、若 , 设直线交直线于点 , 是否存在这样的值,使?若存在,求出此时的值;若不存在,请说明理由.