山东省日照市2023年中考数学试卷

试卷更新日期：2023-07-10 类型：中考真卷

进入出卷网下载

一、单选题

1. 计算： $2 - (- 3)$ 的结果是（　　）

A、5 B、1 C、-1 D、-5

查看试题解析
2. 窗花是贴在窗子或窗户上的剪纸，是中国古老的传统民间艺术之一．下列窗花作品既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 芯片内部有数以亿计的晶体管，为追求更高质量的芯片和更低的电力功耗，需要设计4积更小的晶体管．目前，某品牌手机自主研发了最新型号芯片，其晶体管栅极的宽度为0.000000014米，将数据0.000000014用科学记数法表示为（）

A、 $1.4 \times 1 0^{- 8}$ B、 $14 \times 1 0^{- 7}$ C、 $0.14 \times 1 0^{- 6}$ D、 $1.4 \times 1 0^{- 9}$

查看试题解析
4. 如图所示的几何体的俯视图可能是（）

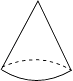A、 B、 C、 D、

查看试题解析
5. 在数学活动课上，小明同学将含 $30 °$ 角的直角三角板的一个顶点按如图方式放置在直尺上，测得 $∠ 1 = 23 °$ ，则 $∠ 2$ 的度数是（）．

A、 $23 °$ B、 $53 °$ C、 $60 °$ D、 $67 °$

查看试题解析
6. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(- 2 m^{2})}^{3} = - 8 m^{6}$ C、 $(x + y)^{2} = x^{2} + y^{2}$ D、 $2 a b + 3 a^{2} b = 5 a^{3} b^{2}$

查看试题解析
7. 《九章算术》是中国古代重要的数学著作，其中“盈不足术”记载：今有共买鸡，人出九，盈十一；人出六，不足十六．问人数鸡价各几何？译文：今有人合伙买鸡，每人出9钱，会多出11钱；每人出6钱，又差16钱．问人数、买鸡的钱数各是多少？设人数为x，可列方程为（）

A、 $9 x + 11 = 6 x + 16$ B、 $9 x - 11 = 6 x - 16$ C、 $9 x + 11 = 6 x - 16$ D、 $9 x - 11 = 6 x + 16$

查看试题解析
8. 日照灯塔是日照海滨港口城市的标志性建筑之一，主要为日照近海及进出日照港的船舶提供导航服务．数学小组的同学要测量灯塔的高度，如图所示，在点B处测得灯塔最高点A的仰角 $∠ A B D = 45 °$ ，再沿 $B D$ 方向前进至C处测得最高点A的仰角 $∠ A C D = 60 °$ ， $B C = 15.3 m$ ，则灯塔的高度 $A D$ 大约是（）（结果精确到 $1 m$ ，参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ）

A、 $31 m$ B、 $36 m$ C、 $42 m$ D、 $53 m$

查看试题解析
9. 已知直角三角形的三边 $a ， b ， c$ 满足 $c > a > b$ ，分别以 $a ， b ， c$ 为边作三个正方形，把两个较小的正方形放置在最大正方形内，如图，设三个正方形无重叠部分的面积为 $S_{1}$ ，均重叠部分的面积为 $S_{2}$ ，则（）

A、 $S_{1} > S_{2}$ B、 $S_{1} < S_{2}$ C、 $S_{1} = S_{2}$ D、 $S_{1} ， S_{2}$ 大小无法确定

查看试题解析
10. 若关于 $x$ 的方程 $\frac{x}{x - 1} - 2 = \frac{3 m}{2 x - 2}$ 解为正数，则 $m$ 的取值范围是（）

A、 $m > - \frac{2}{3}$ B、 $m < \frac{4}{3}$ C、 $m > - \frac{2}{3}$ 且 $m \neq 0$ D、 $m < \frac{4}{3}$ 且 $m \neq \frac{2}{3}$

查看试题解析
11. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + b x (a \neq 0)$ ，满足 ${\begin{array}{l} 3 a + b > 0 \\ a + b < 0 \end{array}$ ，已知点 $(- 3 ， m)$ ， $(2 ， n)$ ， $(4 ， t)$ 在该抛物线上，则m，n，t的大小关系为（）

A、 $t < n < m$ B、 $m < t < n$ C、 $n < t < m$ D、 $n < m < t$

查看试题解析
12. 数学家高斯推动了数学科学的发展，被数学界誉为“数学王子”，据传，他在计算 $1 + 2 + 3 + 4 + ⋯ + 100$ 时，用到了一种方法，将首尾两个数相加，进而得到 $1 + 2 + 3 + 4 + ⋯ + 100 = \frac{100 \times (1 + 100)}{2}$ ．人们借助于这样的方法，得到 $1 + 2 + 3 + 4 + ⋯ + n = \frac{n (1 + n)}{2}$ （n是正整数）．有下列问题，如图，在平面直角坐标系中的一系列格点 $A_{i} (x_{i} ， y_{i})$ ，其中 $i = 1 ， 2 ， 3 ， ⋯ ， n ， ⋯$ ，且 $x_{i} ， y_{i}$ 是整数．记 $a_{n} = x_{n} + y_{n}$ ，如 $A_{1} (0 ， 0)$ ，即 $a_{1} = 0 ， A_{2} (1 ， 0)$ ，即 $a_{2} = 1 ， A_{3} (1 ， - 1)$ ，即 $a_{3} = 0 ， ⋯$ ，以此类推．则下列结论正确的是（）

A、 $a_{2023} = 40$ B、 $a_{2024} = 43$ C、 $a_{(2 n - 1)^{2}} = 2 n - 6$ D、 $a_{(2 n - 1)^{2}} = 2 n - 4$

查看试题解析

二、填空题

13. 分解因式： $a^{3} b - a b =$ .

查看试题解析
14. 若点 $M (m + 3 ， m - 1)$ 在第四象限，则m的取值范围是．

查看试题解析
15. 已知反比例函数 $y = \frac{6 - 3 k}{x}$ （ $k > 1$ 且 $k \neq 2$ ）的图象与一次函数 $y = - 7 x + b$ 的图象共有两个交点，且两交点横坐标的乘积 $x_{1} \cdot x_{2} > 0$ ，请写出一个满足条件的k值．

查看试题解析
16. 如图，矩形 $A B C D$ 中， $A B = 6 ， A D = 8$ ，点P在对角线 $B D$ 上，过点P作 $M N ⊥ B D$ ，交边 $A D ， B C$ 于点M，N，过点M作 $M E ⊥ A D$ 交 $B D$ 于点E，连接 $E N ， B M ， D N$ ．下列结论：① $E M = E N$ ；②四边形 $M B N D$ 的面积不变；③当 $A M ： M D = 1 ： 2$ 时， $S_{△ M P E} = \frac{96}{25}$ ；④ $B M + M N + N D$ 的最小值是20．其中所有正确结论的序号是．

查看试题解析

三、解答题

17.

(1)、化简： $\sqrt{8} - | 1 - \sqrt{2} | + 2^{- 2} - 2 \times s i n 45 °$ ；

(2)、先化简，再求值： $(\frac{x^{2} - 2}{x - 2} - x) \div \frac{x - 1}{x^{2} - 4 x + 4}$ ，其中 $x = - \frac{1}{2}$ ．

查看试题解析

18. 2023年3月22日至28日是第三十届“中国水周”，某学校组织开展主题为“节约用水，共护母亲河”的社会实践活动．A小组在甲，乙两个小区各随机抽取30户居民，统计其3月份用水量，分别将两个小区居民的用水量

x (m^{3})

分为5组，第一组：

5 \leq x < 7

，第二组：

7 \leq x < 9

，第三组：

9 \leq x < 11

，第四组：

11 \leq x < 13

，第五组：

13 \leq x < 15

，并对数据进行整理、描述和分析，得到如下信息：

信息一：

甲小区3月份用水量频数分布表
用水量（x/m）	频数（户）
$5 \leq x < 7$	4
$7 \leq x < 9$	9
$9 \leq x < 11$	10
$11 \leq x < 13$	5
$13 \leq x < 15$	2

信息二：甲、乙两小区3月份用水量数据的平均数和中位数如下：

	甲小区	乙小区
平均数	9.0	9.1
中位数	9.2	a

信息三：乙小区3月份用水量在第三组的数据为：9，9.2，9.4，9.5，9.6，9.7，10，10.3，10.4，10.6．

根据以上信息，回答下列问题：

(1)、

a =

；

(2)、在甲小区抽取的用户中，3月份用水量低于本小区平均用水量的户数所占百分比为

b_{1}

，在乙小区抽取的用户中，3月份用水量低于本小区平均用水量的户数所占百分比为

b_{2}

，比较

b_{1}

，

b_{2}

大小，并说明理由；

(3)、若甲小区共有600户居民，乙小区共有750户居民，估计两个小区3月份用水量不低于

13 m^{3}

的总户数；

(4)、因任务安排，需在B小组和C小组分别随机抽取1名同学加入A小组，已知B小组有3名男生和1名女生，C小组有2名男生和2名女生，请用列表或画树状图的方法，求抽取的两名同学都是男生的概率．

查看试题解析

19. 如图，平行四边形 $A B C D$ 中，点E是对角线 $A C$ 上一点，连接 $B E ， D E$ ，且 $B E = D E$ ．

(1)、求证：四边形 $A B C D$ 是菱形；

(2)、若 $A B = 10 ， t a n ∠ B A C = 2$ ，求四边形 $A B C D$ 的面积．

查看试题解析
20. 要制作200个A，B两种规格的顶部无盖木盒，A种规格是长、宽、高都为 $20 c m$ 的正方体无盖木盒，B种规格是长、宽、高各为 $20 c m$ ， $20 c m$ ， $10 c m$ 的长方体无盖木盒，如图1．现有200张规格为 $40 c m \times 40 c m$ 的木板材，对该种木板材有甲、乙两种切割方式，如图2．切割、拼接等板材损耗忽略不计．

(1)、设制作A种木盒x个，则制作B种木盒个；若使用甲种方式切割的木板材y张，则使用乙种方式切割的木板材张；

(2)、该200张木板材恰好能做成200个A和B两种规格的无盖木盒，请分别求出A，B木盒的个数和使用甲，乙两种方式切割的木板材张数；

(3)、包括材质等成本在内，用甲种切割方式的木板材每张成本5元，用乙种切割方式的木板材每张成本8元．根据市场调研，A种木盒的销售单价定为a元，B种木盒的销售单价定为 $(20 - \frac{1}{2} a)$ 元，两种木盒的销售单价均不能低于7元，不超过18元．在（2）的条件下，两种木盒的销售单价分别定为多少元时，这批木盒的销售利润最大，并求出最大利润．

查看试题解析
21. 在探究“四点共圆的条件”的数学活动课上，小霞小组通过探究得出：在平面内，一组对角互补的四边形的四个顶点共圆．请应用此结论．解决以下问题：
如图1， $△ A B C$ 中， $A B = A C ， ∠ B A C = α$ （ $60 ° < α < 180 °$ ）．点D是 $B C$ 边上的一动点（点D不与B，C重合），将线段 $A D$ 绕点A顺时针旋转 $α$ 到线段 $A E$ ，连接 $B E$ ．

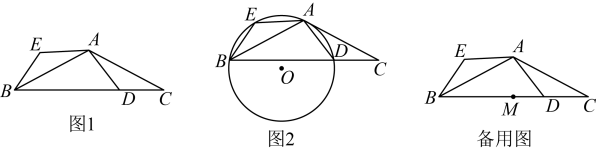(1)、求证：A，E，B，D四点共圆；

(2)、如图2，当 $A D = C D$ 时， $⊙ O$ 是四边形 $A E B D$ 的外接圆，求证： $A C$ 是 $⊙ O$ 的切线；

(3)、已知 $α = 120 ° ， B C = 6$ ，点M是边 $B C$ 的中点，此时 $⊙ P$ 是四边形 $A E B D$ 的外接圆，直接写出圆心P与点M距离的最小值．

查看试题解析
22. 在平面直角坐标系 $x O y$ 内，抛物线 $y = - a x^{2} + 5 a x + 2 (a > 0)$ 交y轴于点C，过点C作x轴的平行线交该抛物线于点D．

(1)、求点C，D的坐标；

(2)、当 $a = \frac{1}{3}$ 时，如图1，该抛物线与x轴交于A，B两点（点A在点B的左侧），点P为直线 $A D$ 上方抛物线上一点，将直线 $P D$ 沿直线 $A D$ 翻折，交x轴于点 $M (4 ， 0)$ ，求点P的坐标；

(3)、坐标平面内有两点 $E (\frac{1}{a} ， a + 1) ， F (5 ， a + 1)$ ，以线段 $E F$ 为边向上作正方形 $E F G H$ ．
①若 $a = 1$ ，求正方形 $E F G H$ 的边与抛物线的所有交点坐标；

②当正方形 $E F G H$ 的边与该抛物线有且仅有两个交点，且这两个交点到x轴的距离之差为 $\frac{5}{2}$ 时，求a的值．

查看试题解析