湖南省张家界市2023年中考数学试卷
试卷更新日期:2023-07-10 类型:中考真卷
一、单选题
-
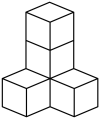
1. 的相反数是( )A、 B、 C、2023 D、2. 如图是由5个完全相同的小正方体组成的立体图形,其主视图是( )
 A、
A、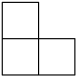 B、
B、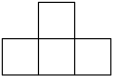 C、
C、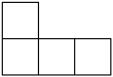 D、
D、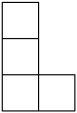 3. 下列运算正确的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、扇形统计图能够清楚地反映事物的变化趋势 B、对某型号电子产品的使用寿命采用全面调查的方式 C、有一种游戏的中奖概率是 , 则做5次这样的游戏一定会有一次中奖 D、甲、乙两组数据的平均数相等,它们的方差分别是 , , 则乙比甲稳定5. 如图,已知直线 , 平分 , , 则的度数是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、扇形统计图能够清楚地反映事物的变化趋势 B、对某型号电子产品的使用寿命采用全面调查的方式 C、有一种游戏的中奖概率是 , 则做5次这样的游戏一定会有一次中奖 D、甲、乙两组数据的平均数相等,它们的方差分别是 , , 则乙比甲稳定5. 如图,已知直线 , 平分 , , 则的度数是( )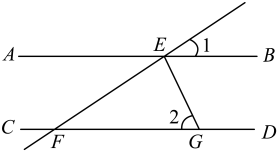 A、 B、 C、 D、6. 《四元玉鉴》是一部成就辉煌的数学名著,是宋元数学集大成者,也是我国古代水平最高的一部数学著作.该著作记载了“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽”.大意是:现请人代买一批椽,这批椽的总售价为文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问文能买多少株椽?设元购买椽的数量为x株,则符合题意的方程是( ).A、 B、 C、 D、7. “莱洛三角形”也称为圆弧三角形,它是工业生产中广泛使用的一种图形.如图,分别以等边的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的封闭图形是“莱洛三角形”.若等边的边长为3,则该“莱洛三角形”的周长等于( )
A、 B、 C、 D、6. 《四元玉鉴》是一部成就辉煌的数学名著,是宋元数学集大成者,也是我国古代水平最高的一部数学著作.该著作记载了“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽”.大意是:现请人代买一批椽,这批椽的总售价为文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问文能买多少株椽?设元购买椽的数量为x株,则符合题意的方程是( ).A、 B、 C、 D、7. “莱洛三角形”也称为圆弧三角形,它是工业生产中广泛使用的一种图形.如图,分别以等边的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的封闭图形是“莱洛三角形”.若等边的边长为3,则该“莱洛三角形”的周长等于( ) A、 B、 C、 D、8. 如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,点D在上,且 , 反比例函数的图象经过点D及矩形的对称中心M,连接 . 若的面积为3,则k的值为( )
A、 B、 C、 D、8. 如图,矩形的顶点A,C分别在y轴、x轴的正半轴上,点D在上,且 , 反比例函数的图象经过点D及矩形的对称中心M,连接 . 若的面积为3,则k的值为( )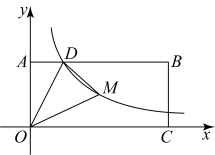 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
9. “仙境张家界,峰迷全世界”,据统计,2023年“五一”节假日期间,张家界市各大景区共接待游客约864000人次.将数据864000用科学记数法表示为 .10. 因式分解: = .11. 关于x的一元二次方程有两个不相等的实数根,则m的取值范围是 .12. 2023年4月24日是我国第八个“中国航天日”,某校开展了一次航天知识竞赛,共选拔8名选手参加总决赛,他们的决赛成绩分别是95,92,93,89,94,90,96,88.则这8名选手决赛成绩的中位数是 .13. 如图,为的平分线,且 , 将四边形绕点逆时针方向旋转后,得到四边形 , 且 , 则四边形旋转的角度是 .
 14. 如图,在平面直角坐标系中,四边形是正方形,点的坐标为 , 是以点为圆心,为半径的圆弧;是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,继续以点 , , , 为圆心按上述作法得到的曲线称为正方形的“渐开线”,则点的坐标是 .
14. 如图,在平面直角坐标系中,四边形是正方形,点的坐标为 , 是以点为圆心,为半径的圆弧;是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,是以点为圆心,为半径的圆弧,继续以点 , , , 为圆心按上述作法得到的曲线称为正方形的“渐开线”,则点的坐标是 .
三、解答题
-
15. 计算: .16. 先化简 , 然后从 , 1,2这三个数中选一个合适的数代入求值.17. 为拓展学生视野,某中学组织八年级师生开展研学活动,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出三辆车,且其余客车恰好坐满.现有甲、乙两种客车,它们的载客量和租金如下表所示:
甲型客车
乙型客车
载客量(人/辆)
45
60
租金(元/辆)
200
300
(1)、参加此次研学活动的师生人数是多少?原计划租用多少辆45座客车?(2)、若租用同一种客车,要使每位师生都有座位,应该怎样租用才合算?18. 如图,已知点A,D,C,B在同一条直线上,且 , , .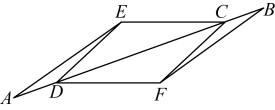 (1)、求证:;(2)、若时,求证:四边形是菱形.19. 2022年4月21日新版《义务教育课程方案和课程标准(2022年版)》正式颁布,优化了课程设置,其中将劳动教育从综合实践活动课程中独立出来.某校为了初步了解学生的劳动教育情况,对九年级学生“参加家务劳动的时间”进行了抽样调查,并将劳动时间x分为如下四组(A:;B:;C:;D: , 单位:分钟)进行统计,绘制了如下不完整的统计图.
(1)、求证:;(2)、若时,求证:四边形是菱形.19. 2022年4月21日新版《义务教育课程方案和课程标准(2022年版)》正式颁布,优化了课程设置,其中将劳动教育从综合实践活动课程中独立出来.某校为了初步了解学生的劳动教育情况,对九年级学生“参加家务劳动的时间”进行了抽样调查,并将劳动时间x分为如下四组(A:;B:;C:;D: , 单位:分钟)进行统计,绘制了如下不完整的统计图.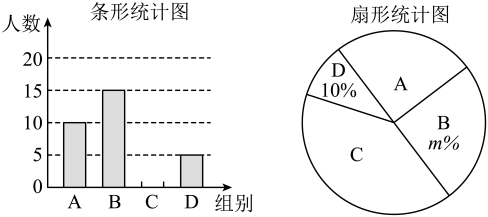
根据以上信息,解答下列问题:
(1)、本次抽取的学生人数为人,扇形统计图中m的值为;(2)、补全条形统计图;(3)、已知该校九年级有600名学生,请估计该校九年级学生中参加家务劳动的时间在80分钟(含80分钟)以上的学生有多少人?(4)、若D组中有3名女生,其余均是男生,从中随机抽取两名同学交流劳动感受,请用列表法或树状图法,求抽取的两名同学中恰好是一名女生和一名男生的概率.20. “游张家界山水,逛七十二奇楼”成为今年旅游新特色.某数学兴趣小组用无人机测量奇楼的高度,测量方案如图:先将无人机垂直上升至距水平地面225m的P点,测得奇楼顶端A的俯角为 , 再将无人机沿水平方向飞行200m到达点Q,测得奇楼底端B的俯角为 , 求奇楼的高度.(结果精确到1m,参考数据: , , )
 21. 阅读下面材料:
21. 阅读下面材料:将边长分别为a, , , 的正方形面积分别记为 , , , .
则
例如:当 , 时,
根据以上材料解答下列问题:
(1)、当 , 时, , ;(2)、当 , 时,把边长为的正方形面积记作 , 其中n是正整数,从(1)中的计算结果,你能猜出等于多少吗?并证明你的猜想;(3)、当 , 时,令 , , , …, , 且 , 求T的值.

