浙江省宁波市江北区2022-2023学年八年级下册数学期末考试试卷

试卷更新日期：2023-07-10 类型：期末考试

进入出卷网下载

一、选择题（每小题4分，共40分，在每小题给出的四个选项中，只有一项符合题目要求）

1. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{4}$ B、 $\sqrt{7}$ C、 $\sqrt{\frac{1}{5}}$ D、 $\sqrt{0.3}$

查看试题解析
2. 下列计算正确的是（）

A、 $2 \sqrt{2} - \sqrt{2} = 2$ B、 $\sqrt{25} = \pm 5$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{5}$ D、 $(\sqrt{3})^{2} = 3$

查看试题解析
3. 用配方法解一元二次方程 $x^{2} + 4 x - 1 = 0$ 时，原方程可变形为（）

A、 $(x + 2)^{2} = 1$ B、 $(x + 2)^{2} = 5$ C、 $(x - 2)^{2} = 1$ D、 $(x + 4)^{2} = 17$

查看试题解析
4. 甲，乙两用户去年上半年每月电费支出情况的折线统计图如下所示，根据统计图所呈现的两组数据，则统计量方差 $S_{甲}^{2}$ 和 $S_{乙}^{2}$ 的大小关系是（）

A、 $S_{甲}^{2} < S_{乙}^{2}$ B、 $S_{甲}^{2} = S_{乙}^{2}$ C、 $S_{甲}^{2} > S_{乙}^{2}$ D、无法确定

查看试题解析
5. 如图，点 $A$ 在反比例函数 $y = \frac{k}{x} (k \neq 0 ， x < 0)$ 图象上， $A B ⊥ x$ 轴于点 $B$ ，若 $△ A O B$ 的面积为2，则 $k$ 的值为（）

A、 $- 4$ B、4 C、 $- 2$ D、2

查看试题解析
6. 用反证法证明“在 $△ A B C$ 中，若 $A B = A C$ ，则 $∠ B < 90 °$ ”时，以下三个步骤正确的排列顺序是（）
步骤如下：
①假设在△ABC中，∠B≥90° .
②因此假设不成立，：∴∠B<90°.
③由AB=AC，得∠B=∠C≥90°，即∠B+∠C≥180°，∴∠A+∠B+∠C> 180°，这与“三角形三个内角的和等于180°”产生矛盾.

A、①③② B、①②③ C、③①② D、③②①

查看试题解析
7. 某放射性元素经2天后，质量衰变为原来的 $\frac{1}{2}$ ．若设这种放射性元素质量的日平均减少率为 $x$ ，则可列出方程为（）

A、 $1 - 2 x = \frac{1}{2}$ B、 $2 (1 - x) = \frac{1}{2}$ C、 $(1 - x)^{2} = \frac{1}{2}$ D、 $\frac{1}{2} (1 - x)^{2} = 1$

查看试题解析
8. 根据以下平行四边形中所标注的角的度数、边的长度，一定能判定其为菱形的是（）

A、 B、 C、 D、

查看试题解析
9. 已知矩形 $A B C D$ 的两条对角线 $A C ， B D$ 交于点 $O$ ．动点 $P$ 从点 $A$ 出发，沿矩形的边按 $A B \to B C$ 的路径匀速运动到点 $C$ ．设点 $P$ 的运动速度为1单位长度/秒，运动时间为 $x$ 秒，线段 $O P$ 的长为 $y ， y$ 与 $x$ 函数关系的大致图象如图所示，其中 $a ， b$ 分别为图象中两段曲线最低点的纵坐标，则 $a + b$ 的值为（）

A、6 B、7 C、8 D、9

查看试题解析
10. 已知实数 $m ， n$ 满足 $m^{2} - m n + n^{2} = 3$ ，设 $P = m^{2} + m n - n^{2}$ ，则 $P$ 的最大值为（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题（每小题5分，共30分）

11. 二次根式 $\sqrt{x - 2}$ 中，字母 $x$ 的取值范围是．

查看试题解析
12. 十二边形的外角和为°．

查看试题解析
13. 已知关于 $x$ 的一元二次方程 $x^{2} + k x - 1 = 0$ 的一个根是2，则 $k$ 的值为．

查看试题解析
14. 已知反比例函数 $y = \frac{3}{x}$ ，当 $- 3 \leq y < - 1$ 时，自变量 $x$ 的取值范围是．

查看试题解析
15. 如图，在正方形 $A B C D$ 中， $A B = 5$ ，点 $E ， F$ 分别在线段 $A D ， B D$ 上，且 $D E = 2$ ，过点 $F$ 作 $F G ⊥ F E$ 与边 $A B$ 交于点 $G$ ．当 $A G = G F$ 时， $B F$ 的长为．

查看试题解析
16. 如图，在平面直角坐标系中，平行四边形 $O A B C$ 的边 $A B$ 与反比例函数 $y = \frac{4}{x} (x > 0)$ 的图象交于 $A ， D$ 两点，且与 $y$ 轴正半轴交于点 $B$ ，点 $C$ 在反比例函数 $y = \frac{k}{x} (k < 0 ， x < 0)$ 的图象上．若点 $D$ 是 $A B$ 的中点，则平行四边形 $O A B C$ 的面积为， $k =$ ．

查看试题解析

三、解答题（本大题有8小题，共80分）

17. 计算：

(1)、 $\sqrt{8} - 2 \sqrt{2} + \sqrt{\frac{1}{2}}$

(2)、 $(\sqrt{3} - 1) \times \sqrt{3} - \sqrt{(- 3)^{2}} + \frac{6}{\sqrt{3}}$

查看试题解析
18. 解方程：

(1)、 $(x - 3)^{2} = 9$

(2)、 $x^{2} - 2 x - 15 = 0$

查看试题解析
19. 下列三个 $3 \times 4$ 的网格图均由相同的小菱形组成，每个网格图中有3个小菱形已涂上阴影，请在余下的空白小菱形中，分别按要求选取一个涂上阴影：

(1)、使得4个阴影小菱形组成的图形是轴对称图形，但不是中心对称图形．

(2)、使得4个阴影小菱形组成的图形是中心对称图形，但不是轴对称图形．

(3)、使得4个阴影小菱形组成的图形既是中心对称图形，又是轴对称图形．

查看试题解析
20. 已知：如图1，在平行四边形 $A B C D$ 中，连结 $B D ， ∠ D B C = 90 °$ ，点 $E$ ， $F$ 分别为 $D C ， B C$ 的中点，连结 $E F$ 并延长交 $A B$ 的延长线于点 $G$ ．

(1)、如图1，若 $B C = 3 ， B D = 4$ ，求四边形 $B G E D$ 的周长．

(2)、如图2，连结 $B E ， C G$ ．求证：四边形 $B G C E$ 是菱形．

查看试题解析
21. 为了了解八年级学生的课外阅读情况，学校随机调查了该年级两个班级各50名学生，获得他们在某一周双休日课外阅读时间（记为t，单位：时）的两组样本数据，并整理绘制成如下条形统计图与扇形统计图．

(1)、分别求出 $t = 3$ 时班级一与班级二相应的学生人数，并补全条形统计图．

(2)、由以上统计图提供的数据，并根据已学习的统计量（如平均数、中位数、众数、方差、标准差）知识，写出两条关于这两个班级学生课外阅读情况比较分析的结论．

(3)、学校倡导鼓励学生课外阅读，并计划提出学生课外阅读的一个适当时间建议．你认为这个适当时间定为几小时 $(t = ?)$ 对同学们而言比较合适？并请运用统计知识简要说明理由．

查看试题解析
22. 如图，反比例函数 $y = \frac{k_{1}}{x} (k_{1} \neq 0)$ 的图象与一次函数 $y = k_{2} x + b (k_{2} \neq 0)$ 的图象相交于点 $A (1 ， 4)$ 与点 $B (m ， - 1)$ ，连结 $A O ， B O$ ．

(1)、求一次函数与反比例函数的表达式．

(2)、求 $△ A O B$ 的面积．

(3)、利用图象，直接写出关于 $x$ 的不等式 $k_{2} x + b \leq \frac{k_{1}}{x}$ 的解集．

查看试题解析
23. 年糕饺是宁波的特色美食，其以年糕为皮，可咸可甜的馅料裹于其中，口感软糯平实．今有某店铺销售年糕饺，通过分析销售情况发现，年糕饺的日销售量y（盒）是销售单价x（元/盒）的一次函数，销售单价、日销售量的部分对应值如下表，已知销售单价不低于成本价．当店铺将销售单价定为18元/盒时，日销售利润为750元．
销售单价x（元/盒）
15
17
日销售量y（盒）
150
100

(1)、求年糕饺的日销售量y（盒）关于销售单价x（元/盒）的函数表达式．

(2)、求年糕饺每盒的成本价．

(3)、端午节，为了尽可能让利顾客，扩大销售，店铺采用了降价促销的方式，当销售单价x（元/盒）定为多少时，日销售利润为1000元？

查看试题解析
24. 如图1，在菱形 $A B C D$ 中， $∠ B A D = 60 °$ ．等腰 $△ M E F$ 的两个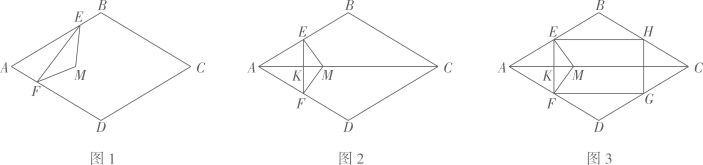顶点 $E ， F$ 分别在 $A B ， A D$ 上，且 $∠ E M F = 120 °$ ，点 $A ， M$ 在 $E F$ 的异侧．

(1)、如图2，当 $E F ⊥ A C$ 于点 $K$ 时，
①求证： $A E = A F$ ，且点 $M$ 在菱形 $A B C D$ 的对角线 $A C$ 上．

②如图3，若 $E H ∥ A C$ 交 $B C$ 于点 $H ， F G ∥ A C$ 交 $C D$ 于点 $G$ ，连结 $G H$ ．当 $\frac{A B}{E M} =$ 时，四边形 $E H G F$ 为正方形．

(2)、如图1，
①判断：点 $M$ ▲ 菱形 $A B C D$ 的对角线 $A C$ 上．（填“在”或“不在”）

②若 $A B = 6 \sqrt{3} ， E M = 4$ ，请求出 $C M$ 的取值范围．

查看试题解析

销售单价x（元/盒）	15	17
日销售量y（盒）	150	100