江西省抚州市南城县2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-10 类型:期中考试
一、单选题
-
1. 下列四个图形中,中心对称图形是( )A、
 B、
B、 C、
C、
D、
D、 2. 以下各组数为三角形的三条边长,其中是直角三角形的三条边长的是( )A、2,3,4 B、3,4,5 C、4,5,6 D、5,6,73. 不等式的正整数解有( )A、5个 B、4个 C、3个 D、2个4. 如图,中, , , 是角平分线,若 , 则线段的长为( )
2. 以下各组数为三角形的三条边长,其中是直角三角形的三条边长的是( )A、2,3,4 B、3,4,5 C、4,5,6 D、5,6,73. 不等式的正整数解有( )A、5个 B、4个 C、3个 D、2个4. 如图,中, , , 是角平分线,若 , 则线段的长为( ) A、1 B、 C、2 D、35. 如图,将绕点A顺时针旋转角110°得到 , 若点E恰好在的延长线上,则等于( )
A、1 B、 C、2 D、35. 如图,将绕点A顺时针旋转角110°得到 , 若点E恰好在的延长线上,则等于( ) A、55° B、70° C、80° D、110°6. 如图,在第一个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2 , 使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2到A3 , 使得A2A3=A2D;…,按此做法进行下去,则第5个三角形中,以点A4为顶点的等腰三角形的底角的度数为( )
A、55° B、70° C、80° D、110°6. 如图,在第一个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2 , 使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2到A3 , 使得A2A3=A2D;…,按此做法进行下去,则第5个三角形中,以点A4为顶点的等腰三角形的底角的度数为( )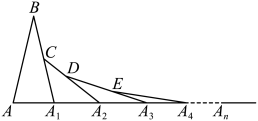 A、5° B、10° C、15° D、25°
A、5° B、10° C、15° D、25°二、填空题
-
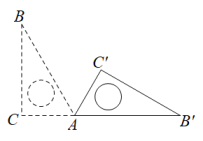
7. 已知等腰三角形的顶角的度数为108°,则底角的度数为 .8. 若点是第二象限的点,则a的取值范围是 .9. 如图,将直角三角板ABC绕顶点A顺时针旋转到 , 点恰好落在CA的延长线上,∠B=30°,∠C=90°,则=°
 10. 如图,在平面直角坐标系中, 的顶点A,B的坐标分别为 , ,把 沿x轴向右平移得到 ,如果点D的坐标为 ,则点E的坐标为.
10. 如图,在平面直角坐标系中, 的顶点A,B的坐标分别为 , ,把 沿x轴向右平移得到 ,如果点D的坐标为 ,则点E的坐标为.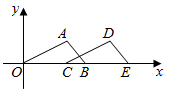 11. 如图,是等边边上的中线,的垂直平分线交于点 , 交于点 , 若 , 则的长为 .
11. 如图,是等边边上的中线,的垂直平分线交于点 , 交于点 , 若 , 则的长为 . 12. 如图,中, , , , 动点从点出发沿射线以的速度运动,设运动时间为 , 当为等腰三角形时,的值为 .
12. 如图,中, , , , 动点从点出发沿射线以的速度运动,设运动时间为 , 当为等腰三角形时,的值为 .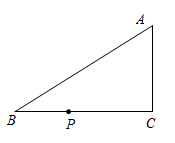
三、解答题
-
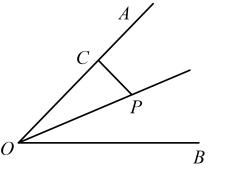
13.(1)、解不等式:(2)、如图,点P在的角平分线上,过点P作 , 交于点C,且 , 求点P到的距离.
 14. 解下列不等式组 , 并把它的解集表示在数轴上.15. 如图,等边三角形ABC和等边三角形ECD的边长相等,BC与CD两边在同一直线上,请根据如下要求,用无刻度的直尺通过连线的方式画图.
14. 解下列不等式组 , 并把它的解集表示在数轴上.15. 如图,等边三角形ABC和等边三角形ECD的边长相等,BC与CD两边在同一直线上,请根据如下要求,用无刻度的直尺通过连线的方式画图. (1)、在图①中画一个直角三角形;(2)、在图②中画出∠ACE的平分线.16.
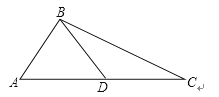
(1)、在图①中画一个直角三角形;(2)、在图②中画出∠ACE的平分线.16.如图,已知△ABC中,AB=BD=DC,∠ABC=105°,求∠A,∠C度数.
 17. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,的三个顶点、、均在格点上.
17. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,的三个顶点、、均在格点上.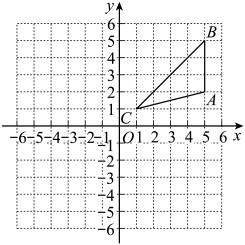 (1)、将向下平移5个单位得到 , 并写出点的坐标;(2)、画出绕点逆时针旋转后得到的 , 并写出点的坐标.18. 已知关于 , 的二元一次方程组 的解满足 ,其中 是非负整数,求 的值.19. “疫情就是命令、防控就是责任”!抚州市南城县某公司在疫情复工准备工作中,计划同时购买一定数量的甲、乙品牌消毒液,若购进甲品牌消毒液20瓶和乙品牌消毒液10瓶,共需资金1300元;若购进甲品牌消毒液10瓶和乙品牌消毒液10瓶,共需资金800元.(1)、甲、乙品牌消毒液的单价分别是多少元?(2)、该公司计划购进甲、乙品牌消毒液共50瓶,而可用于购买这两种商品的资金不超过1900元,且要求购买甲品牌消毒液的数量不少于乙品牌消毒液数量的一半.试问:该公司有几种购买方案?20. 如图,在和中, , , 、相交于点E.
(1)、将向下平移5个单位得到 , 并写出点的坐标;(2)、画出绕点逆时针旋转后得到的 , 并写出点的坐标.18. 已知关于 , 的二元一次方程组 的解满足 ,其中 是非负整数,求 的值.19. “疫情就是命令、防控就是责任”!抚州市南城县某公司在疫情复工准备工作中,计划同时购买一定数量的甲、乙品牌消毒液,若购进甲品牌消毒液20瓶和乙品牌消毒液10瓶,共需资金1300元;若购进甲品牌消毒液10瓶和乙品牌消毒液10瓶,共需资金800元.(1)、甲、乙品牌消毒液的单价分别是多少元?(2)、该公司计划购进甲、乙品牌消毒液共50瓶,而可用于购买这两种商品的资金不超过1900元,且要求购买甲品牌消毒液的数量不少于乙品牌消毒液数量的一半.试问:该公司有几种购买方案?20. 如图,在和中, , , 、相交于点E. (1)、试说明的理由;(2)、若 , , , 求的长.21. 如图,已知函数y1=x+5的图象与x轴交于点A,一次函数y2=-2x+b的图象分别与x轴、y轴交于点B,C,且与y1=x+5的图象交于点D(m,4).
(1)、试说明的理由;(2)、若 , , , 求的长.21. 如图,已知函数y1=x+5的图象与x轴交于点A,一次函数y2=-2x+b的图象分别与x轴、y轴交于点B,C,且与y1=x+5的图象交于点D(m,4). (1)、求m,b的值;(2)、若y1>y2 , 则x的取值范围是 ;(3)、求四边形AOCD的面积.22. 如图,点O是等边三角形内一点,将绕点C顺时针旋转得到 , 连接 .
(1)、求m,b的值;(2)、若y1>y2 , 则x的取值范围是 ;(3)、求四边形AOCD的面积.22. 如图,点O是等边三角形内一点,将绕点C顺时针旋转得到 , 连接 . (1)、求证:;(2)、若 , , , 求的度数.23. 阅读情境:在综合实践课上,同学们探究“全等的等腰直角三角形图形变化问题”.
(1)、求证:;(2)、若 , , , 求的度数.23. 阅读情境:在综合实践课上,同学们探究“全等的等腰直角三角形图形变化问题”.如图1, , 其中 , , 此时,点与点重合.
 (1)、操作探究1:小凡将图1中的两个全等的和按图2方式摆放,点落在上,所在直线交所在直线于点 , 连结 , 求证: .(2)、操作探究2:小彬将图1中的绕点按逆时针方向旋转角度 , 然后,分别延长、 , 它们相交于点 . 如图3,在操作中,小彬提出如下问题,请你解答:
(1)、操作探究1:小凡将图1中的两个全等的和按图2方式摆放,点落在上,所在直线交所在直线于点 , 连结 , 求证: .(2)、操作探究2:小彬将图1中的绕点按逆时针方向旋转角度 , 然后,分别延长、 , 它们相交于点 . 如图3,在操作中,小彬提出如下问题,请你解答:①时,求证:为等边三角形;
②当 时, . (直接回答即可)
(3)、操作探究3:小颖将图1中的绕点A按顺时针方向旋转角度 , 线段和相交于点 , 当旋转到点是边的中点时(可利用图4画图),直接写出线段的长为 .