湖南省长沙市雅礼教育集团2022-2023学年八年级下学期数学期中考试试卷
试卷更新日期:2023-07-10 类型:期中考试
一、单选题
-
1. 下列各曲线中,表示y是x的函数的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、a2+a3=a5 B、3-2=1 C、(x2)3=x5 D、m5÷m3=m23. “桃花春色暖先开,明媚谁人不看来”,每年4月橘子洲的桃花竞相开放,灿若云霞,芳香四溢,吸引众多市民和游客前来赏花踏春.桃花花粉直径约为0.00003米,其中0.00003用科学记数法表示为( )A、 B、 C、 D、4. 若一次函数 的图象经过点 , ,则 与 的大小关系是( )A、 B、 C、 D、5. 如图,在中, , D为的中点,若 , 则的度数为( )
2. 下列计算正确的是( )A、a2+a3=a5 B、3-2=1 C、(x2)3=x5 D、m5÷m3=m23. “桃花春色暖先开,明媚谁人不看来”,每年4月橘子洲的桃花竞相开放,灿若云霞,芳香四溢,吸引众多市民和游客前来赏花踏春.桃花花粉直径约为0.00003米,其中0.00003用科学记数法表示为( )A、 B、 C、 D、4. 若一次函数 的图象经过点 , ,则 与 的大小关系是( )A、 B、 C、 D、5. 如图,在中, , D为的中点,若 , 则的度数为( ) A、55° B、35° C、45° D、30°6. 数形结合是解决数学问题常用的的思想方法.如图,一次函数与一次函数的图象交于点 , 根据图象可知,关于x的不等式的解集是( )
A、55° B、35° C、45° D、30°6. 数形结合是解决数学问题常用的的思想方法.如图,一次函数与一次函数的图象交于点 , 根据图象可知,关于x的不等式的解集是( ) A、 B、 C、 D、7. 如图,在直角坐标系中,菱形 的顶点A , B , C在坐标轴上,若点B的坐标为 , ,则点D的坐标为( )
A、 B、 C、 D、7. 如图,在直角坐标系中,菱形 的顶点A , B , C在坐标轴上,若点B的坐标为 , ,则点D的坐标为( )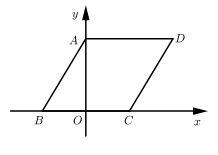 A、 B、 C、 D、8. 下列说法中不正确的是( ).A、矩形的对角线互相垂直且相等 B、平行四边形的对角线互相平分 C、四条边相等的四边形是菱形 D、正方形的对角线相等9. 我国古代数学著作《九章算术》记载了一道有趣的问题.原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设芦苇的长度是x尺.根据题意,可列方程为( )
A、 B、 C、 D、8. 下列说法中不正确的是( ).A、矩形的对角线互相垂直且相等 B、平行四边形的对角线互相平分 C、四条边相等的四边形是菱形 D、正方形的对角线相等9. 我国古代数学著作《九章算术》记载了一道有趣的问题.原文是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.译为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,水的深度与这根芦苇的长度分别是多少?设芦苇的长度是x尺.根据题意,可列方程为( ) A、(x-1)2+52=x2 B、x2+102=(x+1)2 C、(x-1)2+102=x2 D、x2+52=(x+1)210. 如图,在中, , P为边上一动点,于E,于F,动点P从点B出发,沿着匀速向终点C运动,则线段的值大小变化情况是( )
A、(x-1)2+52=x2 B、x2+102=(x+1)2 C、(x-1)2+102=x2 D、x2+52=(x+1)210. 如图,在中, , P为边上一动点,于E,于F,动点P从点B出发,沿着匀速向终点C运动,则线段的值大小变化情况是( ) A、一直增大 B、不变 C、先减小后增大 D、先增大后减小
A、一直增大 B、不变 C、先减小后增大 D、先增大后减小二、填空题
-
11. 分解因式: .12. 函数 中,自变量x的取值范围是 .13. 如图,在中,AD=10,对角线AC与BD相交于点O , AC+BD=22,则△BOC的周长为
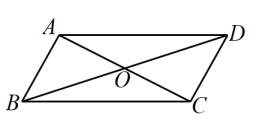 14. 平面直角坐标系中,点 到原点的距离是.15. 对于非零实数a,b,规定 . 若 , 则x的值为 .16. 如图,在四边形中, , , 点 , , , 分别为边 , , , 的中点,连接 , , 则的值为 .
14. 平面直角坐标系中,点 到原点的距离是.15. 对于非零实数a,b,规定 . 若 , 则x的值为 .16. 如图,在四边形中, , , 点 , , , 分别为边 , , , 的中点,连接 , , 则的值为 .
三、解答题
-
17. 计算: .18. 先化简,再求值: , 其中.19. 已知:一次函数y=(3-m)x+m-5.(1)、若一次函数的图象过原点,求实数m的值;(2)、当一次函数的图象经过第二、三、四象限时,求实数m的取值范围.20. 今年是毛泽东等老一辈革命家为雷锋同志题词60周年,为深入贯彻落实党的二十大精神,大力弘扬宣传雷锋精神,某学校举行了以“传承雷锋精神,争当追锋少年”为主题的知识竞赛活动,竞赛满分为10分,学生成绩平均在7分以上,将成绩10分、9分、8分、7分,分别定为A,B,C,D四个等级.学校随机抽取部分学生的竞赛成绩绘制统计图,请回答下列问题:
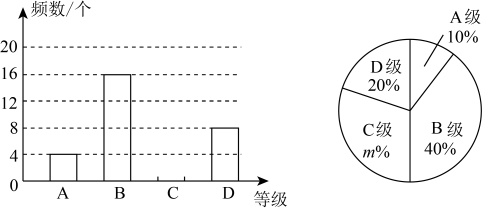 (1)、学校随机抽取的学生人数为;(2)、补全条形统计图;(3)、在扇形统计图中,“C”部分所对应的圆心角的度数为度;(4)、如果该校共有学生人,且规定等级为A、B的为优秀,请估计该校学生在此次知识竞赛活动中成绩为优秀的有多少人?21. 如图,一次函数的图象与轴相交于点 , 与过点的一次函数的图象相交于点 .
(1)、学校随机抽取的学生人数为;(2)、补全条形统计图;(3)、在扇形统计图中,“C”部分所对应的圆心角的度数为度;(4)、如果该校共有学生人,且规定等级为A、B的为优秀,请估计该校学生在此次知识竞赛活动中成绩为优秀的有多少人?21. 如图,一次函数的图象与轴相交于点 , 与过点的一次函数的图象相交于点 .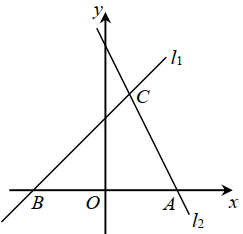 (1)、求一次函数图象相应的函数表达式;(2)、求的面积.22. 如图,在四边形ABCD中,AB//DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE。
(1)、求一次函数图象相应的函数表达式;(2)、求的面积.22. 如图,在四边形ABCD中,AB//DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE。
 (1)、求证:四边形ABCD是菱形;(2)、若AB= ,BD=2,求OE的长.23. 4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然正气”.某书店计划在“世界读书日”前夕,同时购进A,B两类图书,已知购进1本A类图书和2本B类图书共需135元;购进3本A类图书和4本B类图书共需305元.(1)、A,B两类图书每本的进价各是多少元?(2)、该书店计划购进A,B两类图书共90本,且A类图书的购进数量不少于B类图书的购进数量的 . 已知A类图书每本的售价为40元,B类图书每本的售价为58元,求如何进货才能使书店所获利润最大,最大利润为多少元?24. 在平面直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“吉祥点”.(1)、求函数的图象上所有“吉祥点”的坐标;(2)、证明:无论k为何值,函数( , k为常数)的图象总经过一个确定的“吉祥点”;(3)、若直线l:与直线 , 直线分别交于点A,B,直线与直线交于点C.记线段围成的区域(不含边界)为W.若区域W内没有“吉祥点”,直接写出k的取值范围.25. 如图,平面直角坐标系中,矩形的对角线 , ,
(1)、求证:四边形ABCD是菱形;(2)、若AB= ,BD=2,求OE的长.23. 4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然正气”.某书店计划在“世界读书日”前夕,同时购进A,B两类图书,已知购进1本A类图书和2本B类图书共需135元;购进3本A类图书和4本B类图书共需305元.(1)、A,B两类图书每本的进价各是多少元?(2)、该书店计划购进A,B两类图书共90本,且A类图书的购进数量不少于B类图书的购进数量的 . 已知A类图书每本的售价为40元,B类图书每本的售价为58元,求如何进货才能使书店所获利润最大,最大利润为多少元?24. 在平面直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“吉祥点”.(1)、求函数的图象上所有“吉祥点”的坐标;(2)、证明:无论k为何值,函数( , k为常数)的图象总经过一个确定的“吉祥点”;(3)、若直线l:与直线 , 直线分别交于点A,B,直线与直线交于点C.记线段围成的区域(不含边界)为W.若区域W内没有“吉祥点”,直接写出k的取值范围.25. 如图,平面直角坐标系中,矩形的对角线 , , (1)、求B点的坐标;(2)、把矩形沿直线对折使点C落在点A处,与相交于点F,求四边形的周长;(3)、若点M在坐标轴上,平面内是否存在点N,使以O、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
(1)、求B点的坐标;(2)、把矩形沿直线对折使点C落在点A处,与相交于点F,求四边形的周长;(3)、若点M在坐标轴上,平面内是否存在点N,使以O、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.