湖南省株洲市茶陵县2022-2023学年八年级下学期数学期中考试试卷

试卷更新日期：2023-07-10 类型：期中考试

进入出卷网下载

一、单选题

1. 在 $R t △ A B C$ ，两条直角边长分别为6和8，则斜边长为（）

A、6 B、7 C、10 D、5

查看试题解析
2. 湖南革命烈士纪念塔的塔底平面为八边形，这个八边形的内角和（）

A、 $720 °$ B、 $900 °$ C、 $1080 °$ D、 $1440 °$

查看试题解析
3. 在四边形 $A B C D$ 中，下列不能判断它是平行四边形的是（）

A、 $A B ∥ C D$ ， $A D ∥ B C$ B、 $A B = C D ， A D = B C$ C、 $A B ∥ C D$ ， $A B = C D$ D、 $A B ∥ C D$ ， $A D = B C$

查看试题解析
4. 依次连接菱形四条边的中点，得到的中点四边形是（　　）

A、梯形 B、矩形 C、菱形 D、正方形

查看试题解析
5. 如图，小红家的木门左下角有一点受潮，她想检测门是否变形，准备采用如下方法：先测量门的边 $A B$ 和 $B C$ 的长，再测量点A和点C间的距离，由此可推断 $∠ B$ 是否为直角，这样做的依据是（）

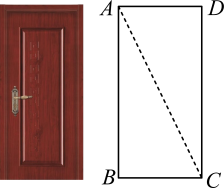A、勾股定理 B、勾股定理的逆定理 C、三角形内角和定理 D、直角三角形的两锐角互余

查看试题解析
6. 下列命题中，是真命题的是（）

A、四条边相等的四边形是正方形 B、对角线相互垂直的四边形是平行四边形 C、对角线相等且相互平分的四边形是矩形 D、对角线相等且相互垂直的四边形是菱形

查看试题解析
7. 如图，已知 $∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 = 290 °$ ，那么 $∠ 5$ 的大小是（）

A、 $60 °$ B、 $70 °$ C、 $80 °$ D、 $90 °$

查看试题解析
8. 点 $M (m + 1 ， m + 3)$ 在x轴上，则M点坐标为（）

A、 $(0 ， - 4)$ B、 $(4 ， 0)$ C、 $(- 2 ， 0)$ D、 $(0 ， - 2)$

查看试题解析
9. 我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，它是由四个全等的直角三角形与中间的小正方形 $E F G H$ 拼成的一个大正方形 $A B C D$ ，连接 $A C$ ，交 $B E$ 于点 $P$ ，如图所示，若正方形 $A B C D$ 的面积为 $28$ ， $A E + E B = 7$ ，则 $S_{△ C F P} - S_{△ A E P}$ 的值是（　　）

A、3 B、3.5 C、4 D、7

查看试题解析
10. 如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥ CD于点F，连接EF，给出下列五个结论：① AP＝EF；② AP⊥ EF；③∠PFE＝∠BAP；④ PD＝EC；⑤ PB²+PD²＝2PA² ，正确结论是（　　）

A、① ③ B、① ② ③ C、① ③ ⑤ D、① ② ③ ⑤

查看试题解析

二、填空题

11. 点 $P (3 ， 2)$ 关于原点O的对称点 $P^{'}$ 的坐标是.

查看试题解析
12. 如图，平行四边形 $A B C D$ 添加一个条件使得它成为矩形.（任意添加一个符合题意的条件即可）

查看试题解析
13. 如图，在 $▱ A B C D$ 中，∠ABC的平分线BE交AD于E，BC＝5，AB＝3，则DE的长为

查看试题解析
14. 如图，菱形的边长是10，对角线BD的长是16，点H是边AD的中点，则OH的长是．

查看试题解析
15. 小明在操场上从A点出发，沿直线前进10米后向左转45°，再沿直线前进10米后，又向左转45°，照这样走下去，他第一次回到出发地A点时，一共走了米．

查看试题解析
16. 如图， $△ A B C$ 的顶点都在边长为1的正方形网格上． $B D ⊥ A C$ 于点D，则 $B D =$ ．

查看试题解析
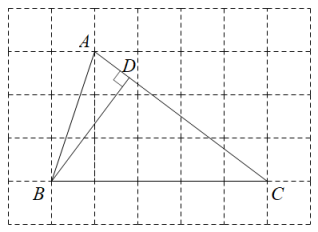17. 如图，将矩形纸片ABCD沿EF折叠，使点D与点B重合，AD＝6cm，AB＝2cm，则DE的长cm．

查看试题解析
18. 四边形具有不稳定性，对于四条边长确定的四边形，当内角度数发生变化时，其形状也会随之改变．如图，改变边长为2的正方形ABCD的内角，变为菱形 $A B C^{'} D^{'}$ ，若 $∠ D^{'} A B = 45 °$ ，则阴影部分的面积是．

查看试题解析

三、解答题

19. 根据图中相关数据，求出 $x$ 的值．

查看试题解析
20. 如图，已知 $△ A B C$ 中 $A B = A C$ ， $B C = 10$ ， $D$ 是 $A C$ 上一点，且 $C D = 6$ ， $B D = 8$ ．

(1)、求证： $△ B D C$ 是直角三角形；

(2)、求 $A B$ 的长．

查看试题解析
21. 如图，在菱形ABCD中， $∠ A B C = 60 °$ ，周长为48cm，求：

(1)、两对角线AC和BD的长度；

(2)、菱形ABCD的面积．

查看试题解析
22. 在平面直角坐标系xOy中，把△ABC向右平移5个单位长度，再向上平移3个单位长度，得到△A₁B₁C₁ ．

(1)、画出平移后的△A₁B₁C₁；

(2)、写出△A₁B₁C₁三个顶点A₁、B₁、C₁的坐标．

(3)、求△ABC的面积．

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ C A B$ ，交 $C B$ 于点D，过点D作 $D E ⊥ A B$ 于点E

(1)、求证： $△ A C D ≌ △ A E D$ ；

(2)、若 $∠ B = 30 °$ ， $C D = 5$ ，求 $B D$ 的长．

查看试题解析
24. 如图：在菱形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 交于点O，过点A作 $A E ⊥ B C$ 于点E，延长 $B C$ 至点F，使 $C F = B E$ ，连接 $D F$ ．

(1)、求证：四边形 $A E F D$ 是矩形；

(2)、若 $B F = 16$ ， $D F = 8$ ，求 $C D$ 的长．

查看试题解析
25. 已知当 $m$ ， $n$ 都是实数，且满足 $2 m = 8 + n$ 时，称 $p (m - 1 ， \frac{n + 2}{2})$ 为“好点”．

(1)、判断点 $A$ $(\frac{3}{2} ， - \frac{1}{2})$ ， $B (4 ， 10)$ 是否为“好点”，并说明理由；

(2)、若点 $M$ $(a ， 2 a - 1)$ 是“好点”，请判断点 $M$ 在第几象限？并说明理由．

查看试题解析
26. 如图，在矩形ABCD中，AC＝60 cm ， ∠BAC＝60°，点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动，同时点F从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点E ， F运动的时间是t秒(0<t≤15)．过点F作OF⊥BC于点O ，连接OE ， EF.

(1)、求证：AE＝OF；

(2)、四边形AEOF能够成为菱形吗？如果能，求出相应的t值，如果不能，请说明理由；

(3)、当t为何值时，△OEF为直角三角形？请说明理由．

查看试题解析