北师大版数学九年级上册同步练习——第一章《特殊平行四边形》1.菱形的性质与判定(3)
试卷更新日期:2023-07-10 类型:同步测试
一、选择题
-
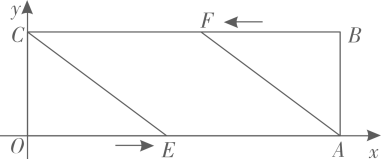
1. 已知菱形ABCD的面积是12,对角线AC=4,则BD是( )A、10 B、8 C、6 D、32. 如图,在平面直角坐标系中,点的坐标为 , 点的坐标为 , 以为边作矩形 . 动点分别从点同时出发,以每秒1个单位长度的速度沿向终点移动.当移动时间为4秒时,的值为( )
 A、 B、 C、 D、3. 如图,菱形中, , , 是对角线上的任意一点,则的最小值为( ).
A、 B、 C、 D、3. 如图,菱形中, , , 是对角线上的任意一点,则的最小值为( ). A、 B、 C、2 D、4. 一个平行四边形的一条边长为7,两条对角线的长分别是10和 , 则这个平行四边形的面积为( )A、 B、 C、35 D、5. 如图,将矩形对折,使边与 , 与分别重合,展开后得到四边形 . 若 , , 则四边形的面积为( )
A、 B、 C、2 D、4. 一个平行四边形的一条边长为7,两条对角线的长分别是10和 , 则这个平行四边形的面积为( )A、 B、 C、35 D、5. 如图,将矩形对折,使边与 , 与分别重合,展开后得到四边形 . 若 , , 则四边形的面积为( ) A、2 B、4 C、5 D、66. 如图,在的两边上分别截取、 , 使;分别以点A、B为圆心,长为半径作弧,两弧交于点C;连接、、、 . 若 , 四边形的面积为 . 则的长为( )
A、2 B、4 C、5 D、66. 如图,在的两边上分别截取、 , 使;分别以点A、B为圆心,长为半径作弧,两弧交于点C;连接、、、 . 若 , 四边形的面积为 . 则的长为( ) A、 B、 C、 D、7. 如图,在菱形ABCD中,对角线 , 点E、F分别是边AB、BC的中点,点P在AC上运动和过程中,的最小值是( )
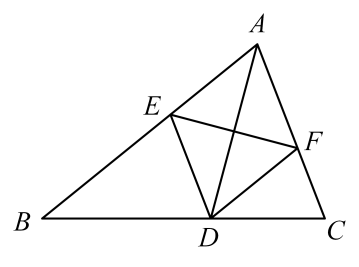
A、 B、 C、 D、7. 如图,在菱形ABCD中,对角线 , 点E、F分别是边AB、BC的中点,点P在AC上运动和过程中,的最小值是( )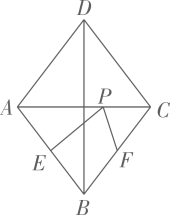 A、3 B、4 C、5 D、68. 如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC,AD于点F、G,连接OG,则下列结论正确的是( )
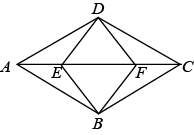
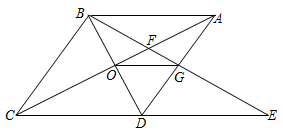
A、3 B、4 C、5 D、68. 如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC,AD于点F、G,连接OG,则下列结论正确的是( )①;②与EGD全等的三角形共有2个;③S四边形ODEG=S四边形ABOG;④由点A、B、D、E构成的四边形是菱形;
 A、①③④ B、①④ C、①②③ D、②③④
A、①③④ B、①④ C、①②③ D、②③④二、填空题
-
9. 如图,在四边形ABCD中, , 于点O.请添加一个条件: , 使四边形ABCD成为菱形.
 10. 如图, , 分别以A,B为圆心,长为半径画弧,两弧相交于M,N两点.连接 , 则四边形的面积为 .
10. 如图, , 分别以A,B为圆心,长为半径画弧,两弧相交于M,N两点.连接 , 则四边形的面积为 .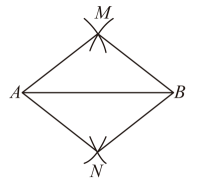 11. 如图,菱形的边长为2, , 对角线与交于点 , 为中点,为中点,连接 , 则的长为 .
11. 如图,菱形的边长为2, , 对角线与交于点 , 为中点,为中点,连接 , 则的长为 .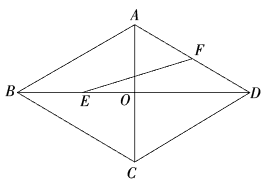 12. 如图,菱形 的对角线 , 相交于点O, , ,则菱形 的周长为.
12. 如图,菱形 的对角线 , 相交于点O, , ,则菱形 的周长为.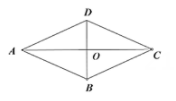 13. 如图,在菱形ABCD中, , ,Q为AB的中点,P为对角线BD上的任意一点,则 的最小值为.
13. 如图,在菱形ABCD中, , ,Q为AB的中点,P为对角线BD上的任意一点,则 的最小值为. 14. 如图,在菱形中, , . 点E、F同时从A、C两点出发,分别沿 , 方向向点匀速移动(到点即停止).点的速度为 , 点的速度为 , 经过后恰为等边三角形,则此时的值为 .
14. 如图,在菱形中, , . 点E、F同时从A、C两点出发,分别沿 , 方向向点匀速移动(到点即停止).点的速度为 , 点的速度为 , 经过后恰为等边三角形,则此时的值为 .
三、解答题
-
15. 如图,在中,平分 , 交于点E , 交于点F . 求证: .
 16. 如图,在 中, , 于点 , 平分 ,分别交 、 于点 、 , 于点 ,连接 ,求证:四边形 是菱形.
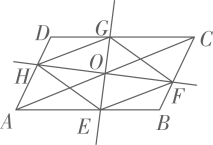
16. 如图,在 中, , 于点 , 平分 ,分别交 、 于点 、 , 于点 ,连接 ,求证:四边形 是菱形. 17. 如图,过的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.
17. 如图,过的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.