2023年浙教版数学八年级上册2.6 直角三角形 同步测试(培优版)
试卷更新日期:2023-07-09 类型:同步测试
一、选择题(每题3分,共30分)
-
1. 如图,中, , , 分别以点 , 为圆心,大于长为半径作弧,两弧交于点 , , 以为圆心,长为半径作弧,与直线交于点 , 与交于点 , 若 , 则的长为( )
 A、 B、 C、 D、2. 如图,Rt△ABC中, ∠ACB=90°,∠A=30°,CD⊥AB于D,CE是△ABC的中线,要说明“三个角分别对应相等的两个三角形全等”是假命题,可以作为反例的两个三角形是( )
A、 B、 C、 D、2. 如图,Rt△ABC中, ∠ACB=90°,∠A=30°,CD⊥AB于D,CE是△ABC的中线,要说明“三个角分别对应相等的两个三角形全等”是假命题,可以作为反例的两个三角形是( ) A、△ACE和△BCE B、△BCE和△ABC C、△CDE 和△BCD D、△ACD和△BCD3. 如图,中, , , 尺规作图痕迹如下.
A、△ACE和△BCE B、△BCE和△ABC C、△CDE 和△BCD D、△ACD和△BCD3. 如图,中, , , 尺规作图痕迹如下.结论Ⅰ:点一定为的内心;
结论Ⅱ:连接 , , 则 .
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
 A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对,Ⅱ对 D、Ⅰ对,Ⅱ不对4. 如图,在等腰三角形中, , , 是底边上的高,在的延长线上有一个动点D,连接 , 作 , 交的延长线于点E,的角平分线交边于点F,则在点D运动的过程中,线段的最小值( )
A、Ⅰ和Ⅱ都对 B、Ⅰ和Ⅱ都不对 C、Ⅰ不对,Ⅱ对 D、Ⅰ对,Ⅱ不对4. 如图,在等腰三角形中, , , 是底边上的高,在的延长线上有一个动点D,连接 , 作 , 交的延长线于点E,的角平分线交边于点F,则在点D运动的过程中,线段的最小值( )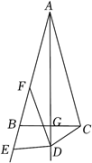 A、6 B、4 C、3 D、25. 如图,在中,已知 , , 的垂直平分线交于点D.若 , 则( ).
A、6 B、4 C、3 D、25. 如图,在中,已知 , , 的垂直平分线交于点D.若 , 则( ). A、2 B、3 C、4 D、2.86. 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,BE⊥AC,CF⊥AB,垂足分别为E,F.则下列四个结论:①AD上任意一点到点C,B的距离相等;②AD上任意一点到边AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF;⑤BC=AD.其中,正确的个数为( )
A、2 B、3 C、4 D、2.86. 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,BE⊥AC,CF⊥AB,垂足分别为E,F.则下列四个结论:①AD上任意一点到点C,B的距离相等;②AD上任意一点到边AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF;⑤BC=AD.其中,正确的个数为( ) A、2个 B、3个 C、4个 D、5个7. 如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC上一点,且AD=AE,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )
A、2个 B、3个 C、4个 D、5个7. 如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC上一点,且AD=AE,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )①BF=CF;②若BE⊥AC,则CF=DF;③若BE平分∠ABC,则FG=;④连结EF,若BE⊥AC,则∠DFE=2∠ABE.
 A、①②③ B、③④ C、①②④ D、①②③④8. 若等腰三角形一腰上的高与腰长之比为 , 则该等腰三角形顶角的度数为( )A、或 B、 C、 D、9. 如图,在锐角 中, , , 是 内的两点, 平分 , ,若 , ,则 的长度是( )
A、①②③ B、③④ C、①②④ D、①②③④8. 若等腰三角形一腰上的高与腰长之比为 , 则该等腰三角形顶角的度数为( )A、或 B、 C、 D、9. 如图,在锐角 中, , , 是 内的两点, 平分 , ,若 , ,则 的长度是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空4分,共24分)
-
10. 如图,在锐角三角形ABC中,°,的平分线交BC于点D,M,N分别是AD和AB上的动点,当取得最小值时, .
 11. 如图,线段AB=4,E为AB中点,点C、D为直线AB同侧不重合的两点,且∠ACB=∠ADB=90°,连接CE、DE、CD,设△CDE的面积为S,则S的范围是.
11. 如图,线段AB=4,E为AB中点,点C、D为直线AB同侧不重合的两点,且∠ACB=∠ADB=90°,连接CE、DE、CD,设△CDE的面积为S,则S的范围是. 12. 已知等腰 中, 于点D,且 ,则 底角的度数为.13. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,点E,N,M分别是线段AB,AC,EB的中点,下列结论:①△NMC为等边三角形.②CE⊥MN;③S△ABC=2S四边形ENCM;④AN= EM.其中正确的是 .
12. 已知等腰 中, 于点D,且 ,则 底角的度数为.13. 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,点E,N,M分别是线段AB,AC,EB的中点,下列结论:①△NMC为等边三角形.②CE⊥MN;③S△ABC=2S四边形ENCM;④AN= EM.其中正确的是 . 14. 如图,△ABC中,∠B=45°,∠C=75°,AB=4,D为BC上一动点,过D作DE⊥AC于点E,作DF⊥AB于点F,连接EF,则EF的最小值为.
14. 如图,△ABC中,∠B=45°,∠C=75°,AB=4,D为BC上一动点,过D作DE⊥AC于点E,作DF⊥AB于点F,连接EF,则EF的最小值为. 15. 如图所示,∠AOB=60°,点P是∠AOB内一定点,并且OP=2,点M、N分别是射线OA,OB上异于点O的动点,当△PMN的周长取最小值时,点O到线段MN的距离为.
15. 如图所示,∠AOB=60°,点P是∠AOB内一定点,并且OP=2,点M、N分别是射线OA,OB上异于点O的动点,当△PMN的周长取最小值时,点O到线段MN的距离为.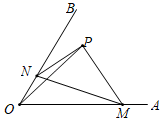
三、解答题(共5题,共66分)
-
16. 在△ABC中,∠C=90°,∠A=30°,BC=2,以AB为边作等边△ABD,点E为线段AD的中点,连接CE,请画出图形,并直接写出线段CE的长.17. 如图,在中,∠C=90°,∠A=30°,BC=12cm.动点P从点A出发,沿AB向点B运动,动点Q从点B出发,沿BC向点C运动,如果动点P以2cm/s,Q以1cm/s的速度同时出发,设运动时间为t(s),解答下列问题:
 (1)、t为多少时,是等边三角形?(2)、P、Q在运动过程中,的形状不断发生变化,当t为多少时,是直角三角形?请说明理由.18. 如图1,在中,分别是边上的高线,M,N分别是线段的中点.
(1)、t为多少时,是等边三角形?(2)、P、Q在运动过程中,的形状不断发生变化,当t为多少时,是直角三角形?请说明理由.18. 如图1,在中,分别是边上的高线,M,N分别是线段的中点. (1)、求证:.(2)、连接 , 猜想与之间的关系,并说明理由.(3)、若将锐角三角形变为钝角三角形 , 其余条件不变,如图2,直接写出与之间的关系.19. 定义:如果三角形的两个内角α与β满足α+2β=100°,那么我们称这样的三角形为“奇妙三角形”.
(1)、求证:.(2)、连接 , 猜想与之间的关系,并说明理由.(3)、若将锐角三角形变为钝角三角形 , 其余条件不变,如图2,直接写出与之间的关系.19. 定义:如果三角形的两个内角α与β满足α+2β=100°,那么我们称这样的三角形为“奇妙三角形”. (1)、如图1,中,∠ACB=80°,BD平分∠ABC.求证:为“奇妙三角形”;(2)、若为“奇妙三角形”,且∠C=80°.求证:是直角三角形;(3)、如图2,中,BD平分∠ABC,若为“奇妙三角形”,且∠A=40°,直接写出∠C的度数.20. 如图①,在△ABC中,AB=AC=BC=10cm,动点P以每秒1cm的速度从点A出发,沿线段AB向点B运动.设点P的运动时间为t(t>0)秒.(知识储备:一个角是60°的等腰三角形是等边三角形)
(1)、如图1,中,∠ACB=80°,BD平分∠ABC.求证:为“奇妙三角形”;(2)、若为“奇妙三角形”,且∠C=80°.求证:是直角三角形;(3)、如图2,中,BD平分∠ABC,若为“奇妙三角形”,且∠A=40°,直接写出∠C的度数.20. 如图①,在△ABC中,AB=AC=BC=10cm,动点P以每秒1cm的速度从点A出发,沿线段AB向点B运动.设点P的运动时间为t(t>0)秒.(知识储备:一个角是60°的等腰三角形是等边三角形) (1)、当t=5时,求证:△PAC是直角三角形;(2)、如图②,若另一动点Q在线段CA上以每秒2cm的速度由点C向点A运动,且与点P同时出发,点Q到达终点A时点P也随之停止运动.当△PAQ是直角三角形时,直接写出t的值;(3)、如图③,若另一动点Q从点C出发,以每秒1cm的速度沿射线BC方向运动,且与点P同时出发.当点P到达终点B时点Q也随之停止运动,连接PQ交AC于点D,过点P作PE⊥AC于E.在运动过程中,线段DE的长度是否发生变化?若不变,直接写出DE的长度;若变化,说明如何变化.
(1)、当t=5时,求证:△PAC是直角三角形;(2)、如图②,若另一动点Q在线段CA上以每秒2cm的速度由点C向点A运动,且与点P同时出发,点Q到达终点A时点P也随之停止运动.当△PAQ是直角三角形时,直接写出t的值;(3)、如图③,若另一动点Q从点C出发,以每秒1cm的速度沿射线BC方向运动,且与点P同时出发.当点P到达终点B时点Q也随之停止运动,连接PQ交AC于点D,过点P作PE⊥AC于E.在运动过程中,线段DE的长度是否发生变化?若不变,直接写出DE的长度;若变化,说明如何变化.