2023年浙教版数学八年级上册2.6 直角三角形 同步测试(基础版)
试卷更新日期:2023-07-09 类型:同步测试
一、选择题
-
1. 如图,在中, , , 则( )
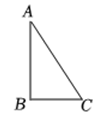 A、 B、 C、 D、2. 直角三角形的斜边上的中线长为4,则它的斜边长为( )A、16 B、8 C、4 D、23. 如图,在中, , , D为BC上一点, , 则BC的长为( )
A、 B、 C、 D、2. 直角三角形的斜边上的中线长为4,则它的斜边长为( )A、16 B、8 C、4 D、23. 如图,在中, , , D为BC上一点, , 则BC的长为( ) A、10 B、12 C、14 D、164. 如图,在中, , , 点在上, , , 则的长为( )
A、10 B、12 C、14 D、164. 如图,在中, , , 点在上, , , 则的长为( ) A、4 B、5 C、6 D、85. 如图,衣架框内部可以近似看成一个等腰三角形,记为等腰三角形 , 若 , 是的中点, , 则的长为( )
A、4 B、5 C、6 D、85. 如图,衣架框内部可以近似看成一个等腰三角形,记为等腰三角形 , 若 , 是的中点, , 则的长为( ) A、 B、 C、 D、6. 如图,在中, , 于点D, , , 则的长为( )
A、 B、 C、 D、6. 如图,在中, , 于点D, , , 则的长为( ) A、4 B、6 C、8 D、107. 如图, , , 则、和的关系是( )
A、4 B、6 C、8 D、107. 如图, , , 则、和的关系是( ) A、 B、 C、 D、8. 如图,在中, , 平分 , 交于点D,若点D恰好在边的垂直平分线上,则∠C的度数为( )
A、 B、 C、 D、8. 如图,在中, , 平分 , 交于点D,若点D恰好在边的垂直平分线上,则∠C的度数为( ) A、30 B、36 C、40 D、459. 如图,AB⊥BD,DE⊥BD,垂足分别为B、D,如果∠A=25°,BC=CD,那么下列结论中,错误的是( )
A、30 B、36 C、40 D、459. 如图,AB⊥BD,DE⊥BD,垂足分别为B、D,如果∠A=25°,BC=CD,那么下列结论中,错误的是( ) A、∠E=25° B、∠ABC=90° C、∠ACB=25° D、∠CDE=90°10. 如图,在中,平分 , 是高,若 , , 则的度数为( )
A、∠E=25° B、∠ABC=90° C、∠ACB=25° D、∠CDE=90°10. 如图,在中,平分 , 是高,若 , , 则的度数为( ) A、30° B、10° C、40° D、20°11. 如图,在等腰三角形ABC中,AB=AC,BD⊥AC,∠ABC=70°,则∠DBC=( )
A、30° B、10° C、40° D、20°11. 如图,在等腰三角形ABC中,AB=AC,BD⊥AC,∠ABC=70°,则∠DBC=( ) A、20° B、30° C、50° D、70°12. 如图,已知 , 于点 , 若 , 则的度数是( )
A、20° B、30° C、50° D、70°12. 如图,已知 , 于点 , 若 , 则的度数是( ) A、30° B、40° C、50° D、60°
A、30° B、40° C、50° D、60°二、填空题
-
13. 已知直角三角形斜边上的中线是2.5cm,斜边上的高是2cm,则这个直角三角形的面积是cm2 .14. Rt△ABC中,锐角 , 则另一个锐角=.15. 将两块全等的直角三角板如图放置,其中一块三角板的斜边恰好经过另一块三角板的直角顶点及斜边上的中点 , 若这两块三角板的斜边长为 , 则.
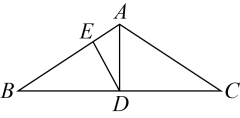
 16. 如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为 .
16. 如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为 . 17. 直角三角形最小的一个外角为度18. 如图, , 点是上一点,点与点关于对称,于点 , 若 , 则的长为 .
17. 直角三角形最小的一个外角为度18. 如图, , 点是上一点,点与点关于对称,于点 , 若 , 则的长为 .
三、解答题
-
19. 如图,在中, , , 于点D,于点E, , 求的长.
 20. 如图,在中, , , 垂足为D,平分.已知 , , 求的度数.
20. 如图,在中, , , 垂足为D,平分.已知 , , 求的度数. 21. 如图,在中, , 垂足为点 , , , 求的度数.
21. 如图,在中, , 垂足为点 , , , 求的度数. 22. 如图,△ABC中,CD、BE分别是高,M、N分别是线段BC、DE的中点.求证:MN⊥DE.
22. 如图,△ABC中,CD、BE分别是高,M、N分别是线段BC、DE的中点.求证:MN⊥DE.


