2023年浙教版数学八年级上册2.4等腰三角形的判定定理同步测试（基础版）

试卷更新日期：2023-07-09 类型：同步测试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 已知△ABC的周长为m，BC=m-2AB，则下列直线一定为△ABC的对称轴的是（）

A、△ABC的边BC上的中线所在的直线 B、∠ACB的平分线所在的直线 C、△ABC的边AB的垂直平分线 D、△ABC的边AC上的高所在的直线

查看试题解析
2. 如图，在 $5 \times 5$ 的正方形网格中，点A、B均在格点上．要在格点上确定一点C，连接 $A C$ 和 $B C$ ，使 $△ A B C$ 是等腰三角形，则网格中满足条件的点C的个数是（　　）

A、5个 B、6个 C、7个 D、8个

查看试题解析
3. 如图，A， $B$ 是池塘两侧端点，在池塘的一侧选取一点 $O$ ，测得 $O A$ 的长为6米， $O B$ 的长为6米， $∠ O = 60 °$ ，则A， $B$ 两点之间的距离是（）

A、4米 B、6米 C、8米 D、10米

查看试题解析
4. 已知，如图， $△ A B C$ 中， $A B = A C$ ， $∠ A = 120 °$ ， $B C = 12 c m$ ， $A B$ 的垂直平分线交 $B C$ 于点M，交 $A B$ 于点E， $A C$ 的垂直平分线交 $B C$ 于点N，交 $A C$ 于点F，则 $M N$ 的长为（）

A、3cm B、4cm C、6cm D、12cm

查看试题解析
5. 在 $△ A B C$ 中， $A B = A C = 6$ ， $∠ B = 6 0^{∘}$ ，则 $△ A B C$ 的周长为（）

A、24 B、18 C、12 D、6

查看试题解析
6. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $∠ A = 15 °$ ，点D是 $A C$ 上一点，连接 $B D ， ∠ D B C = 60 ° ， B D = 4$ ，则 $A D$ 长是（）

A、4 B、5 C、6 D、8

查看试题解析
7. 将一平板保护套展开放置在水平桌面上，其侧面示意图如图所示，若 $∠ A B C = ∠ A C B$ ， $A B = 10 c m$ ，则 $A C$ 的长为（）

A、 $10 c m$ B、 $11 c m$ C、 $12 c m$ D、 $13 c m$

查看试题解析
8. 如图，在△ABC中，AB=AC，D、E是△ABC内的两点，AD平分∠BAC，∠EBC=∠E=60°，若BE=10cm，DE=4cm，则BC的长为（）

A、7cm B、12cm C、14cm D、16cm

查看试题解析
9. 如图所示，以 $∠ A O B$ 的顶点 O 为圆心，适当长为半径画弧，交 $O A$ 于点 C，交 $O B$ 于点 D，再分别以点 C 、 D 为圆心，大于 $\frac{1}{2} C D$ 长为半径画弧，两弧在 $∠ A O B$ 内部交于点 E，过点 E 作射线 $O E$ ，连接 $C D$ $．$ 则下列说法错误的（　　）

A、射线 $O E$ 是 $∠ A O B$ 的平分线 B、 $△ C O D$ 是等腰三角形 C、C、D 两点关于 $O E$ 所在直线对称 D、O、E 两点关于 $C D$ 所在直线对称

查看试题解析
10. 如图，D是 $△ A B C$ 内部的一点， $A D = C D$ ， $∠ B A D = ∠ B C D$ ．下列结论：① $∠ D A C = ∠ D C A$ ；② $A B = A C$ ；③ $B D ⊥ A C$ ；④ $B D$ 平分 $∠ A B C$ ．其中结论正确的序号是（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析

二、填空题（每空4分，共24分）

11. 如图所示，P是等边三角形 $A B C$ 内一点，将 $△ A B P$ 绕点B顺时针方向旋转 $60 °$ ，得到 $△ C B P^{^{'}}$ ，若 $P B = 3$ ，则 $P P^{'} =$ ．

查看试题解析
12. 如图，在 $△ A B E$ 中， $A D ⊥ B E$ 于点D，C是 $B E$ 上一点， $B D = D C$ ，且点C在 $A E$ 的垂直平分线上.若 $△ A B C$ 的周长为30，则 $D E$ 的长为.

查看试题解析
13. 如图， $△ A B C$ 中， $∠ B = ∠ C$ ，点D是 $A B$ 边上一点，过点D作 $D E ⊥ B C$ 交 $B C$ 于点E，交 $C A$ 延长线于点F， $A C = 5$ ， $B D = 3$ ，则 $A F$ 的长为．

查看试题解析
14. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D$ 是 $B C$ 边上的中线，E是 $A B$ 上一点，且 $D E ∥ A C$ ．若 $D E = 3$ ，则 $A B =$ ．

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 30 °$ ， $B C = 6$ ， D为 $A B$ 的中点，P为 $B C$ 上一动点，连接 $A P$ ， $D P$ ，则 $A P + D P$ 的最小值是.

查看试题解析
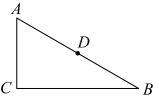16. 如图是某种落地灯的简易示意图， $A B$ 为立杆； $B C$ 为支杆，可绕点B旋转； $D E$ 为悬杆，滑动悬杆可调节 $C D$ 的长度．为了使落地灯更方便学习时的照明，小唯将该落地灯进行了调整，使悬杆的 $C D$ 部分的长度与支杆 $B C$ 相等，且 $∠ B C E = 120 °$ ．若 $C D$ 的长为 $50 c m$ ，则此时B，D两点之间的距离为 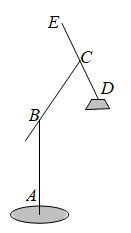$c m$ ．

查看试题解析

三、解答题（共8题，共66分）

17. 如图，在△ABC中，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC交AB于M，交AC于N，若BM＝2，CN＝3，求线段MN的长．

查看试题解析
18. 如图，已知 $∠ A C E$ 是 $△ A B C$ 的一个外角， $C D$ 平分 $∠ A C E$ ，且 $C D ∥ A B$ ，求证： $△ A B C$ 为等腰三角形.

查看试题解析
19. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，把直角边 $B C$ 沿过点 $B$ 的某条直线折叠，使点 $C$ 落到边 $A B$ 上的一点 $D$ 处，当 $∠ A = 30 °$ 时，证明 $B D = D A$ ．

查看试题解析
20. 如图，在 $△ A B C$ 中， $∠ A B C$ 与 $∠ A C B$ 的平分线相交于点O，AO的延长线交 $B C$ 于点D， $O B = O C$ .求证： $B D = C D$ .

查看试题解析
21. 欢欢和父亲起设计一个三角形屋架，如图，父亲给出一组数据：AB＝AC＝7m，BD＝CE＝2.5m，AD＝4m，∠DAE＝60°，让欢欢根据这组数据计算制作这个三角形屋架一共需要多长的钢材，请你帮欢欢计算一下，并说明理由.

查看试题解析
22. 如图，在△ABC中，∠A＝120°，AB＝AC，D是BC的中点，DE⊥AB，DF⊥AC，点E，F为垂足，求证：△DEF是等边三角形．

查看试题解析
23. 如图，在等边△ABC中，点D为边BC上一点，∠ABE＝∠CAD，CF∥BE交AD的延长线于点F.

(1)、求∠AEB的度数；

(2)、若BE＝10，AF＝15，求AE的长.

查看试题解析
24. 如图，已知 $B C ∥ D E$ ，点 $F$ 为 $B D$ 上一点， $C F$ 、 $E F$ 分别平分 $∠ B C E$ 、 $∠ D E C$ ， $E F$ 交 $C B$ 的延长线于点 $A$ ．

(1)、求证 $△ A C E$ 是等腰三角形；

(2)、探索 $B C$ 、 $C E$ 、 $D E$ 之间的等量关系，并说明理由．

查看试题解析

2023年浙教版数学八年级上册2.4等腰三角形的判定定理 同步测试（基础版）

一、选择题（每题3分，共30分）

二、填空题（每空4分，共24分）

三、解答题（共8题，共66分）

2023年浙教版数学八年级上册2.4等腰三角形的判定定理同步测试（基础版）